AMUSIG 破碎和聚结

Simcenter STAR-CCM+ AMUSIG 破碎和聚结模型不适用于颗粒流体。但是，可以使用 AMUSIG 对颗粒流体中的固体颗粒相尺寸分布建模：对于相关应用，运用对聚结和破碎现象的理解和知识，根据需要校准幂次定律聚结和破碎模型。

有一组模型可用于描述不同应用的破碎和聚结过程：

• Luo ([513]) 和 O’Rourke ([524]) 模型适用于湍流聚结。
• Tsouris 和 Tavlarides ([515]) 模型、Martinez-Bazan ([515]) 模型、Kocamustafaogullari ([515]) 模型和 Coulaloglou 和 Eskin ([456]) 模型适用于湍流液体/液体和气泡流破碎。
• 剪切感应破碎和聚结模型适用于层流。
• 此外，对于测试、演示并提供一些用户指定的建模，也可以实施常数和幂次定律模型。

聚结率模型包含碰撞率和聚结效率子模型。破碎率模型包含破碎率和碎片颗粒尺寸分布子模型，可定义给定尺寸颗粒的移除项。所有比率模型都有一个整体标定常数，用户可以根据自身需求调整该常数。临界韦伯数为可调参数，与破碎率模型相关。

单个尺寸组足以对深舱或深塔中上升的稀释泡沫的静水膨胀建模。但是，要使碰撞/破碎研究有意义，建议至少使用三个组。AMUSIG 模型具有自适应性，可以使用少量组研究颗粒尺寸的显著和快速变化。增加组数可能会产生与分辨率无关的结果，作用类似于网格加密。计算成本确定了尺寸组数的实际上限。

层流和湍流破碎模型

破碎过程建模分为两个部分：破碎率和碎片颗粒尺寸分布。破碎率具有时间^-1 维度，因此单个颗粒在时间跨度 $\mathrm{dt}$ 内的破碎概率为（破碎率） $\mathrm{dt}$ 。碎片尺寸分布无量纲。它确定创建的碎片数量和碎片分布。

幂次定律破碎率

此模型适用于湍流破碎和层流破碎。幂次定律破碎率模型描述给定尺寸颗粒的破碎速度。该模型是一个通用模型，针对特定颗粒尺寸 $d$ （按特征直径 $d_0$ 进行比例缩放）下数密度的破碎率乘数 $K_B$ 提供了可调参数。

$$K_B\left(d\right)=C{\left(\frac{d}{d_0}\right)}^a$$

(2244)

由于 $K_B$ 和数密度的乘积是一个比率（以事件/秒/ $m^3$ 为单位），因此标定常数 $C$ 的维度是秒。

此破碎率如同任何其他破碎率一样输入守恒方程：

$$\frac{Dn}{Dt}=-(\mathrm{breakage}\mathrm{rate})*n$$

(2245)

其中：

• ${\epsilon }_f$ 为连续相的湍流耗散率。
• $d_p$ 为颗粒直径。
• $\mathrm{We}$ 为韦伯数。
• ${\mathrm{We}}_{\mathrm{cr}}$ 为临界韦伯数。它确定可以承受给定湍流强度的颗粒尺寸。较大的 ${\mathrm{We}}_{\mathrm{cr}}$ 值表示破碎程度较弱。
• $C_g$ 为可用于调整破碎时间尺度的标定常数。

对于湍流，韦伯数由以下公式给出：

校正因子 ${\left(\frac{{\rho }_p}{{\rho }_f}\right)}^{1/3}$ 表示气泡可以承受的湍流强度大于液滴 [501]。此校正可能会高估气泡直径。但是，可以通过减少临界韦伯数来提高破碎率。

Martinez-Bazan

对于 Eqn. (2246) 中的函数 $f$ ，Martinez-Bazan 模型假设平方根形状。Martinez-Bazan 模型表示低于最小直径时不发生破碎。

Tsouris 和 Tavlarides

对于 Eqn. (2246) 中的函数 $f$ ，Tsouris-Tavlarides 模型使用指数。Tsouris-Tavlarides 模型预测任何液滴都有可能破碎（无最小直径），但破碎概率会随液滴直径呈指数下降。

Coulagloglou-Eskin

Coulaloglou-Eskin 模型预测的尺寸分布范围大于另外两个模型。

Kocamustafaogullari

Kocamustafaogullari 模型适用于对连续气体中的液滴破碎进行建模。该模型考虑液滴内表面张力和粘性力抵抗的变形。此行为的特征度量为韦伯数和奥内佐格数。

对于层流，液滴破碎由毛细管数控制。毛细管数是尝试使液滴变形和破碎的粘性剪切应力与保持液滴球形的毛细管压力之比，由以下公式给出：

其中：

层流破碎模型假设存在临界值 ${Ca}_{cr}$ ，因此对于 ${Ca<Ca}_{cr}$ ，破碎率较小或为零，而对于 ${Ca>Ca}_{cr}$ ，破碎率较大。此临界毛细管数可定义为粘度比率 $\lambda =\frac{{\mu }_d}{{\mu }_c}$ 的函数，其中， ${\mu }_d$ 为离散相的动力粘度：

其中：

对于层流破碎模型，破碎率具有以下结构：

其中：

层流破碎模型之间的区别在于 Eqn. (2250) 中的函数 $f$ 。

克里斯蒂尼 (Cristini)

克里斯蒂尼模型将 $f$ 定义为 ([445])：

$$f=\{\begin{array}{cc}\sqrt{\frac{1}{\mathrm{\Phi }-1}}& ,\mathrm{\Phi }<1\\ 0& ,\mathrm{\Phi }\ge 1\end{array}$$

(2252)

Tsouris 和 Tavlarides

对于 Tsouris 和 Tavlarides 剪切模型，破碎概率随液滴直径呈指数级下降。函数 $f$ 由以下公式给出：

$$f=\exp (-\mathrm{\Phi })$$

(2253)

Coulaloglou 和 Eskin

Coulaloglou 和 Eskin 剪切模型将 $f$ 定义为：

$$f=erfc\left(\sqrt{\mathrm{\Phi }}\right)\sqrt{\frac{4\mathrm{\Phi }}{\pi }}\exp (-\mathrm{\Phi })$$

(2254)

其中 $erfc$ 为补余误差函数。

Kocamustafaogullari

Kocamustafaogullari 模型基于随机二次液滴 (SSD) 模型，其中假设

以下液滴瞬时破碎率：

$$\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{u}\mathrm{p}\mathrm{}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e}=\{\begin{array}{cc}0& ,We\le {We}_{cr}\\ B_1\sqrt{\frac{{\rho }_g}{{\rho }_l}}\frac{w}{Dp}& ,We<{We}_{cr}\end{array}$$

(2255)

其中：

• ${We}_{cr}$ 为临界韦伯数。默认值为 12。
• $B_1$ is a parameter regulating the speed of breakup. Large values signify that breakup occurs later. The default value is $2\sqrt{3}$ .
• ${\rho }_l$ 为液体的密度。
• $Dp$ 为液滴直径。
• ${\rho }_g$ 为气体的密度。
• $w_t$ 为液滴通过连续相的湍流滑移速度。

Kocamustafaogullari ([488]) 通过将 Levich [501] 公式代入湍流液滴的运动方程，关联环形流中液滴尺寸分布的实验数据：

$$\frac{{\rho }_l{D}_p^3}{6}\frac{{du}_l^{\prime }}{dt}=-C_D{\rho }_g\frac{\pi D_p^2}{4}|u_l^{\prime }-u_g^{\prime }|(u_l^{\prime }-u_g^{\prime })$$

(2256)

其中， $u_l^{\prime }$ 和 $u_g^{\prime }$ 分别为液体和气体的波动速度。假设曳力系数为 $C_d=0.5$ ，Eqn. (2256) 随后重新排列如下：

$${\rho }_l(\frac{{dw}_t}{dt}+0.75\frac{{\rho }_g}{{\rho }_l}\frac{w_t}{Dp}{w}_t)=-{\rho }_l\frac{d{u}_g^{\prime }}{dt}$$

(2257)

使用 Kolmogorov 比例缩放并基于非浮力颗粒实验，Kuboi [491] 估计在 λ 比例下气体速度的波动分量如下：

$$|{u_g^{\prime }|}^2=2{\left({ϵ}_g\lambda \right)}^{2/3}$$

(2258)

尺寸为 λ 的气体涡流中的加速度可估计如下：

$$\frac{d{u}_g^{\prime }}{dt}\sim 2\frac{{\left({ϵ}_g\lambda \right)}^{1/3}}{\lambda },\frac{d{w}_t}{dt}\sim \frac{\langle w_t\rangle }{\lambda }$$

(2259)

替换 Eqn. (2256) 中的 Eqn. (2258) 得到：

$$\langle w_t^2\rangle =\frac{2{\left({ϵ}_g\lambda \right)}^{2/3}}{1+0.75\frac{{\rho }_g}{{\rho }_l}\frac{\lambda }{Dp}}$$

(2260)

Eqn. (2260) 在以下条件下达到最大值：

$$\begin{gathered} {\lambda }_{\max }=\frac{8}{3}\frac{{\rho }_l}{{\rho }_g}Dp \\ {\langle {w_t}^2\rangle }_{\max }=\frac{4}{3}{\left(\frac{{\rho }_l{ϵ}_{g}Dp}{3{\rho }_g}\right)}^{2/3} \end{gathered}$$

(2261)

无量纲滑移速度为 $w=\sqrt{\frac{\sigma }{{\rho }_{g}Dp}}W,\langle w\rangle =\sqrt{\frac{\sigma }{{\rho }_{g}Dp}}U,\langle w_t\rangle =\sqrt{\frac{\sigma }{{\rho }_{g}Dp}}r$ ，其中， $W$ and $U$ 为无量纲平均和波动滑移速度。归一化分布由以下公式给出：

$$f\left(w\right)\left(W\right)=\sqrt{\frac{\beta }{\pi }}\frac{W}{U}[\exp (-\beta {(W-U)}^2)-\exp (-\beta {(W+U)}^2\left)\right]$$

(2262)

where $\beta =\frac{3}{2\left({We}_t\right)}$

For zero mean slip, Eqn. (2262) slip reduces to:

(2263)

$$f\left(w\right)\left(W\right)=4\sqrt{\frac{{\beta }^3}{\pi }}{W}^2[\exp (-\beta W^2)$$

(2264)

Kocamustafaogullari has shown that using the characteristic slip velocity given by Eqn. (2256) to Eqn. (2261), it is possible to correlate the available experimental data. Eqn. (2255) is then averaged over all possible realizations of the slip velocity:

$$\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{u}\mathrm{p}\mathrm{}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e}=B_1\{\begin{array}{cc}{\left(\frac{8}{3\pi }\frac{{\rho }_g}{{\rho }_l}\frac{{\langle w}_t^2\rangle }{{Dp}^2}\right)}^{1/2}(1+\beta {We}_{cr})\exp (-\beta {We}_{cr})& ,U=0\\ \sqrt{\frac{{\rho }_g}{{\rho }_l}}\frac{\langle w\rangle }{Dp}& ,U\gg \sqrt{{We}_{cr}}\end{array}$$

(2266)

(2265)

液体粘度影响

液体粘度对破碎率的影响由奥内佐格数 [470] 表征：

$$\mathrm{Oh}=\frac{{\mu }_l}{\sqrt{{\rho }_l{D}_p\sigma }}$$

(2267)

其中， ${\mu }_l$ 为液体粘度， $\sigma$ 为液体的表面张力。

为了考虑更多粘性液滴的增强稳定性，临界韦伯数和奥内佐格数的相关性定义如下：

$${We}_{cr}={We}_{cr|O_h=0}\cdot (1+a{Oh}^b)$$

(2268)

其中， $a$ 和 $b$ 为常数，由格尔丰德在 [464] 中推导得出。

聚结模型

在碰撞率和聚结效率这两个零部件中对聚结过程建模。

湍流碰撞率

仅适用于湍流聚结。聚结率是碰撞率和聚结效率的乘积。湍流碰撞率计算为两个球体（直径分别为 $d_1$ 和 $d_2$ ，并以随机相对速度 $v={\left({ϵ}_f\frac{d_1+d_2}{2}\right)}^{1/3}$ 移动）的碰撞概率。

该模型没有拟合参数，但聚结效率子模型除外。

Luo 聚结效率

Luo 聚结效率模型 ([513]) 假设当接触时间 $t_{contact}$ 大于 $t_{rupture}$ 时发生聚结，需要该时间才能使分离两个气泡的液膜破碎：

$$\mathrm{C}\mathrm{o}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{}\mathrm{E}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}\sim \exp (-C\frac{t_{rupture}}{t_{contact}})$$

(2269)

其中， $C$ 是该模型的唯一标定常数。 $C$ 较大表示无聚结；默认值为 $C=1$ 。

O'Rourke 聚结效率

O’Rourke 聚结效率模型 ([524]) 用于检测连续气相中的液滴碰撞。碰撞的液滴会因连续相的湍流波动发生混乱运动。碰撞结果由碰撞韦伯数控制：

$${\text{We}}_{\text{coll}}=\frac{{\rho }_l{\left(w\right)}^2(r_1+r_2)}{2\sigma }$$

(2270)

其中：

• $r_i,i=1,2,\mathrm{..}$ 为液滴半径。
• $\sigma =\frac{1}{2}({\sigma }_1+{\sigma }_2)$ 为液滴 1 和 2 的平均表面张力。
• ${\rho }_l=\frac{1}{2}({\rho }_1+{\rho }_2)$ 为平均密度。
• $w$ 为两个液滴的相对速度，仅受在 Eqn. (2261) 中计算的湍流波动影响。

碰撞的结果基于影响参数 $B$ 和撞韦伯数 $\text{We}$ 。每对相互作用液滴的碰撞韦伯数 ${\text{We}}_{\text{coll}}$ 可由 Eqn. (2270) 计算。碰撞效率 $E$ 是由获得给定结果的概率定义的 ( $E=B\cdot B$ )。

液滴尺寸比率 $\gamma$ 如下：

$$\gamma =\frac{r_2}{r_1},r_2>r_1$$

(2271)

液滴直径比率修正定义如下：

$$g\left(\gamma \right)=a_3{\gamma }^3+a_2{\gamma }^2+a_1\gamma +a_0$$

(2272)

其中， $\gamma$ 为液滴大小比。常数的默认值为：

• $a_3=2.4$
• $a_2=-5.76$
• $a_1=6.48$
• $a_0=0$

对于碰撞速度 $w$ 的给定值，无反弹和无分离的概率将简化为以下公式：

$$E_{noseparation}=\text{min}[1.0,\frac{g\left(\gamma \right)}{We}]$$

(2273)

且

$$E_{nobounce}=\text{min}[1.0,{\left(\frac{We}{g\left(\gamma \right)}\right)}^{\frac{1}{3}}]$$

(2274)

聚结概率等于 Eqn. (2273) 与 Eqn. (2274) 的乘积：

$$E_{coal}=\text{min}(\frac{g\left(\gamma \right)}{We},{\left(\frac{We}{g\left(\gamma \right)}\right)}^{\frac{1}{3}})$$

(2275)

然后，通过使用破碎分布函数 Eqn. (2264) 对 Eqn. (2274) 求平均值得到聚结效率：

$${\lambda }_c=\frac{1}{3\sqrt{\pi }{\mathrm{\Phi }}^{1/3}}\left[5\mathrm{\Gamma }\right(\frac{5}{6},\mathrm{\Phi })-6{\mathrm{\Phi }}^{5/6}\cdot \exp (-\mathrm{\Phi }\left)\right]+2\mathrm{\Phi }\cdot erfc\left(\sqrt{\mathrm{\Phi }}\right)$$

(2276)

其中， $\mathrm{\Gamma }$ 为不完整的 gamma 函数， $\mathrm{\Phi }$ 定义如下：

$$\mathrm{\Phi }=\frac{3g\gamma }{8W_{et}}$$

(2277)

其中

$${\mathrm{W}\mathrm{e}}_t=\frac{{\rho }_l\langle w_t^2\rangle (r_1+r_2)}{2\sigma }$$

(2278)

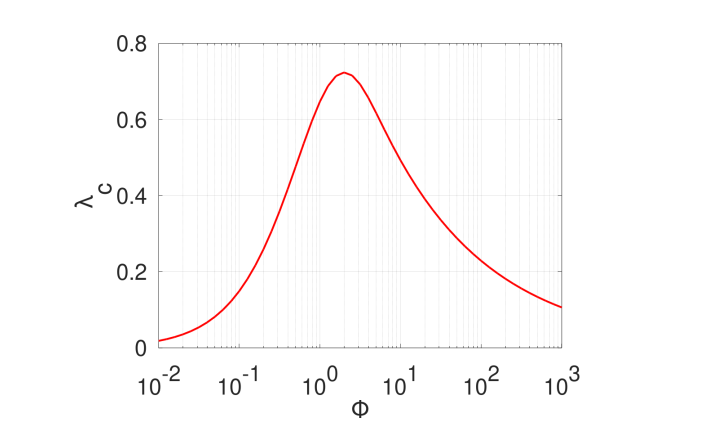
下面绘制了聚结效率图。

当 $\mathrm{\Phi }=1$ 时，效率最大。 $\mathrm{\Phi }\ll 1$ 的区域对应表面张力不稳定导致的高碰撞动能。在此区域中，液滴和聚结效率较低。当 $\mathrm{\Phi }\gg 1$ 时，聚结效率衰减，这是因为两个液滴之间的液滴尺寸比较大 ( $g\left(\gamma \right)\gg 1$ ) 或液滴相对速度较低。

液膜导流聚结效率

液膜导流聚结效率模型是与任何碰撞率模型均兼容的通用模型。

$$\mathrm{C}\mathrm{o}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{}\mathrm{E}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}\sim \exp (-C\frac{{\mathrm{W}\mathrm{e}}^m}{{\mathrm{Re}}^n})$$

(2279)

其中， $\mathrm{W}\mathrm{e}$ 为碰撞韦伯数：

$$\mathrm{W}\mathrm{e}=\frac{\rho U_c^2{d}_{eff}}{\sigma }$$

(2280)

$\mathrm{Re}$ 为碰撞雷诺数：

$$\mathrm{Re}=\frac{\rho U_c{d}_{eff}}{\mu }$$

(2281)

碰撞速度 $U_c$ 由碰撞率模型提供。 $d_{eff}$ 为碰撞液滴或气泡的有效直径。

层流碰撞率

对于层流碰撞率，两个球体的相对速度是由于平均剪切速率所致：

$$v=\dot{S}\frac{d_1+d_2}{2}$$

(2282)

增强的碰撞率幂次定律

此碰撞率模型适用于湍流聚结和层流聚结。

增强的碰撞率幂次定律及其可调参数可用于研究两个尺寸分别为 $d_1$ 和 $d_2$ （按特征直径 $d_0$ 进行比例缩放）的颗粒之间的替代凝结内核 $K$ 。

$$K(d_1,d_2)=C{[{\left(\frac{d_1}{d_0}\right)}^a+{\left(\frac{d_2}{d_0}\right)}^a]}^b{[{\left(\frac{d_1}{d_0}\right)}^c+{\left(\frac{d_2}{d_0}\right)}^c]}^d$$

(2283)

由于内核与两个碰撞尺寸的数密度之积是一个比率（以事件/秒/ $m^3$ 为单位），因此标定常数 $C$ 的维度是 $m^3$ /秒。