本节简要概述OpenFOAM中的有限体积法(Finite Volume Method,FVM)。关于有限体积法的更详细描述,读者可以参考一下相关文献:Ferziger和Peric(2002)、Versteeg and Malalasekra,Weller,Tabor, Jasak及Fureby、Jasak, Jemcov及Tuković、Moukalled, Mangani, Darwish, et al等。
OpenFOAM中非结构有限体积法离散步骤与1.2节中描述的CFD分析步骤有一定的关联。用于定义流体流动的物理属性(如压力、速度或温度/焓等)是数学模型(描述流体流动的偏微分方程组)中的相关变量。
看似不同的物理过程有时可以使用相似的数学模型进行描述,例如热传导过程与水中糖分浓度扩散过程都可以使用扩散模型进行描述。如Ferziger和Peric 2002所描述的通用标量输运方程中包含了用于模拟不同物理过程的项(微分算子),如:流体粒子随流体速度的输运(对流项)、热源(源项)等。由于通用方程中包含了经常遇到的项,因此常用其描述FVM的离散过程。通用输运方程为:
式中, 为待求标量; 为指定的速度向量; 为扩散系数。方程(1.1)中各项从左至右分别为:瞬态项、对流项、扩散项及源项。方程中的每一项都描述了一个以不同方式改变场变量 的物理过程。
有时可以根据物理过程的特性忽略一些项:如对于无粘流体流动,可忽略动量的扩散,因此可以将其从动量方程中去掉。此外出现在某些项中的系数可以是恒定值,也可以是空间和/或时间上变化的物理场,或与介质的物性参数有关。
数值方法的目的为了获取数学模型的近似解。对复杂物理过程进行近似求解是有必要的,因为精确求解通常只能在一些非常特殊的情况下才能得到,而这些特殊情况往往难以应用在工程实际中。
数学模型的近似解通过求解控制方程组的离散近似而得到。有限体积法(FVM)的近似过程涉及使用相应的线性代数方程组替代PDE系统,然后使用计算机进行求解。非结构有限体积法(FVM)生成代数方程组包括两个主要步骤:解域离散和方程离散。
1.3.1 解域离散
数学模型使用连续变量。为了逼近数学模型的解,空间被离散成有限数量的控制体积(网格单元)。这些有限体积(单元)构成了有限体积网格。
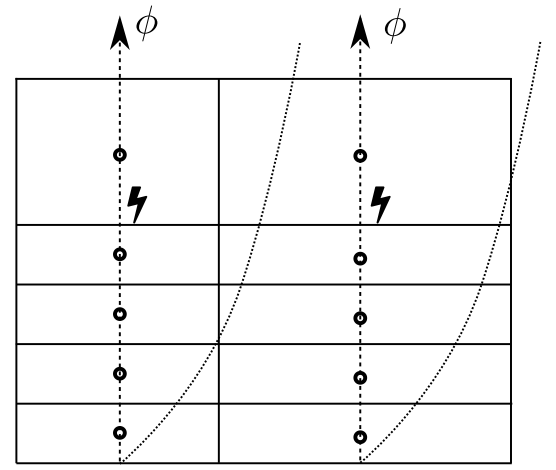
图1.1显示了从连续流体域到离散流体域的转变。
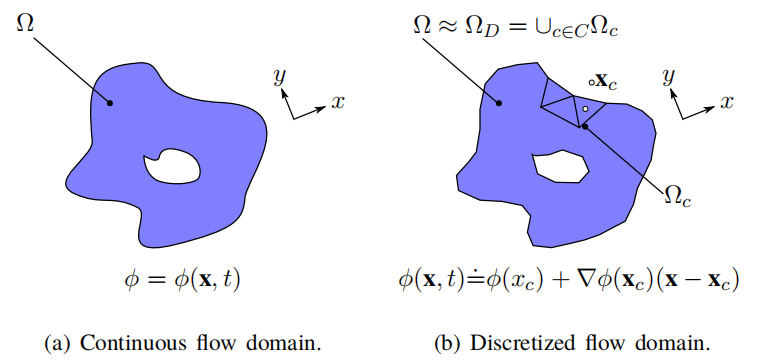
连续流体域近似为网格单元(有限体积)的集合:
其中,为有限体积网格,是离散区域中所有网格索引的集合。在图1.1a中流体填充的空间的每一点上定义的连续物理场在有限体积内被线性近似,如图1.1b所示。
每个有限体积都存储与其中心相关的物理属性(如温度)的体积平均值。将该值与网格中心相关联可使区域离散达到二阶精度。为了解为何会出现这种情况,可以假设物理场可以使用泰勒级数展开为:
引入在点 处定义的量(这些量在 上是恒定的),用式(1.3)中的泰勒级数展开表示网格 内部 的体积平均值,可得到:
体积域的中心定义为:
将式 到式 中,可得到:
由式 可知,对于线性分布的 ,由于其高阶导数为零,因此 在有限体积 上的平均值正好等于 在 的中心 处的值。换句话说,有限体积中心处的单元平均值(以网格为中心)可以准确地恢复线性物理场的值。能精确恢复线性函数值的方法至少具有二阶精度。
注:在网格的中心处得到的单元平均值的非结构FVM的区域离散具有二阶精度。
基于式 的变量 的插值:
式 具有二阶精度,因为式中泰勒级数截断部分的最大项与 成比例。
在式 中,网格中心处的梯度 也必须估计,计算方法在1.3.2节方程离散中会介绍。在理解方程如何离散之前,应当更详细地定义网格 ,特别是网格单元 的相互连接方式,因为这种连接性决定了哪些区域可以离散化。
我们在此区分三种类型的网格:结构网格、块结构网格及非结构网格。这三种网格对区域和方程的离散有不同的要求,并且网格单元相互连接和寻址方式也不同。网格单元之间的连接(网格连通性)决定了相邻单元的访问方式,这对于方程离散非常重要。这进一步影响了在访问网格单元时可能进行的优化,这些优化反映了数值运算的效率以及如何将这些运算并行化。
例如,网格单元的非结构化寻址使得很难在任何特定方向上访问网格单元。这使得在高阶插值格式所需的非结构化网格上构建更大的模板变得复杂,因为它们依赖于来自更宽邻域的单元平均(单元中心)值。使用域分解和消息传递方法对这种依赖单元中心值的高阶插值进行并行化也很复杂,而且可能效率不高,因为必须跨进程边界传递长度可变的大消息。因此,网格的连通性决定了在网格上可以有效地计算什么,有时会产生这样的效果:即为特定的网格选择错误的数值方法所造成的效率低下,使得该方法无法用于实际问题,而这些问题通常需要更多的网格单元。在OpenFOAM中,网格连通性在数值算法的实现方式中也起着非常重要的作用,OpenFOAM仅支持非结构化网格。
结构网格支持对任意网格单元的邻居进行直接寻址以及对网格单元的直接遍历:单元被标记为沿坐标轴方向递增的索引(参见图1.2a)。另一方面,非结构化网格没有明显的方向(见图1.3a)。
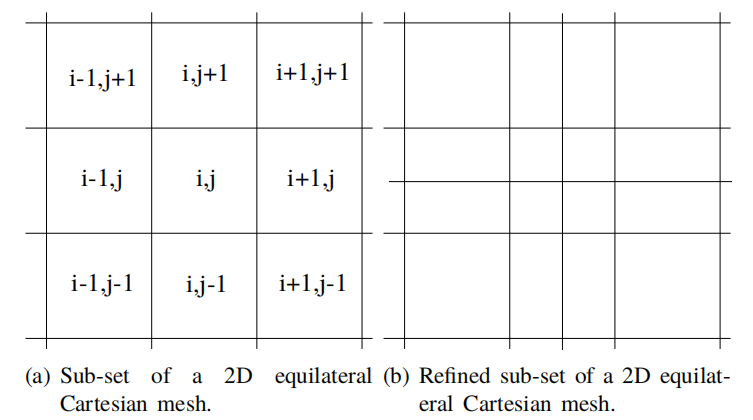
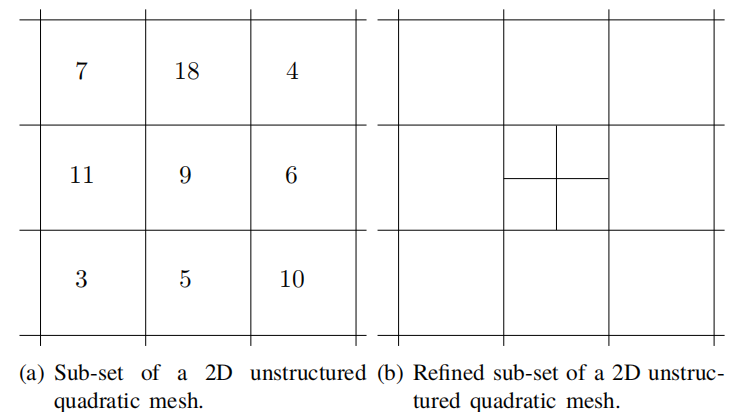
结构网格连通性提高了FVM中涉及的插值的绝对精度,但是当将其用于复杂几何区域的网格生成时,会使网格的灵活性降低。
在网格生成过程中,用户通常希望在解发生较大变化的地方生成密集的网格,而不希望在变量梯度较小的流动区域中浪费网格。所有网格生成步骤应在最短的时间内完成,如果没有实质性的改善,使用结构化网格是无法实现此目的的。对结构网格进行局部网格细化是不可能实现的,因为网格细化必须通过整个网格传播到各自的方向。图1.3b给出了结构网格和非结构网格之间拓扑差异的示意图。
图1.2a显示了一个二维结构网格。这种网格也被称之为笛卡尔网格,因为其由体积中心沿坐标轴方向分布的控制体积组成的。通过改变索引在网格中移动具有一个显著的优势:使用这种网格的数值方法可以通过简单地将索引,递增或递减1来访问任何相邻的网格。例如当通过单元面的通量从单元中心插值到面中心时,可以轻松地应用高阶插值格式以提高求解精度。高阶插值格式意味着将更多的网格单元(不一定与当前网格相邻)包括在插值计算中。
但存在一个问题:在结构网格中进行网格局部细化是很难实现的。
当结构网格上可用的插值阶次仍然不够精确时,在极端变化的区域中常会出现这种情况。例如,在激波模拟或两种不相溶流体的两相流模拟中,会出现物性参数值的显著变化。将它们分开的两种流体之间形成了一个界面,物性参数值可能会存在几个数量级的变化(如气-水界面,密度比约为1000),如图1.4中的示意图所示。
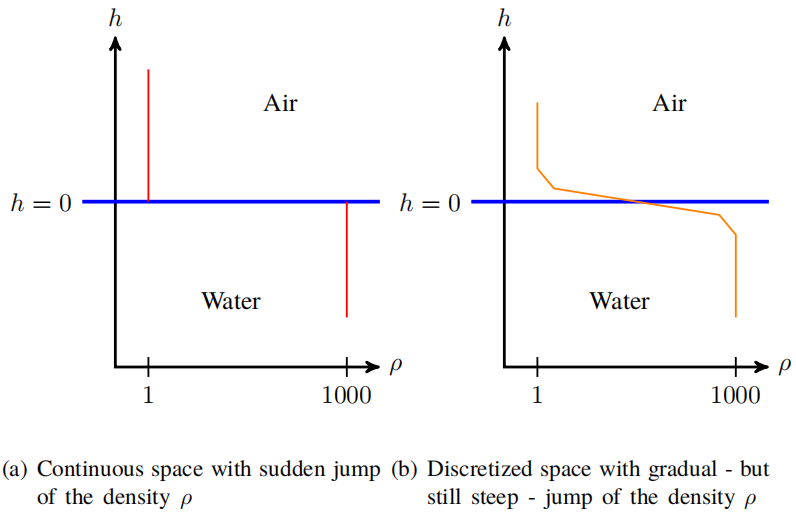
为求解这种数值的急剧变化,需要对网格进行局部细化。这种网格细化既可以在前处理期间完成,也可以在求解计算时进行。如前所述,结构网格的细化不能在局部完成:结构化网格的拓扑结构迫使网格在整个方向上进行细化(请参见图1.2b),其中在两个方向上对单个网格的细化会在整个方向上产生细化。符合弯曲几何形状的结构化网格尤其难以生成,为保持结构网格的连通性,必须对弯曲边界进行参数化,这仅适用于相对简单的几何边界。
然而,结构网格离散在实际应用中有一些扩展,其中一些扩展允许对网格进行局部和动态细化。为了提高局部精度,可以使用块结构细化,这是一个构建由多个结构块组成的网格的过程。当组装这样的块结构网格时,不同的块可以具有不同的网格密度。不幸的是,这引入了新的复杂性,因为数值方法必须能够处理不一致的悬挂节点。或者通过精心地处理结构块,以使不同密度的相邻块上的网格节点完全匹配。即使对于简单的流体域,构建块结构网格也是一个复杂的问题,这往往使得在许多涉及复杂几何形状或边界形状的技术应用中,块结构的网格都不是一个好的选择。细化块结构的网格会导致细化区域扩展到整个块中。使用依赖于边界一致性的块结构网格的标准求解器,细化会使得网格生成更加复杂。
OpenFOAM中的动态自适应局部细化是通过引入额外的数据结构来实现的,这些数据结构产生并存储与网格细化过程相关的信息。这种方法的其中一个例子是基于八叉树的细化,其利用八叉树数据结构将每个结构笛卡尔网格元拆分为八个。这种方法要求网格(或至少是正在细化的网格子集)仅由六面体单元组成。数值插值程序(离散微分算子)使用八叉树数据结构存储信息,并考虑局部网格细化导致的网格拓扑变化。然后可以使用切割单元方法将处理更复杂几何域的可能性添加到八叉树精细结构网格中。在这种情况下,通过边界的分段线性近似来切割弯曲域边界的网格。基于八叉树的自适应网格细化在效率方面具有优势,这取决于在底层结构化网格上执行拓扑操作的方式。然而基于八叉树的细化逻辑要求细化域必须是盒形的。更多关于局部自适应网格细化程序的信息可以在[文献](8 “Tomasz Plewa, Timur Linde, and V Gregory Weirs. Adaptive mesh refinement-theory and applications. Vol. 41. Springer, 2005, pp. 3–5.”)中找到。
OpenFOAM实现了一个支持任意非结构网格的二阶收敛的FVM。除了非结构化网格的连通性之外,任意非结构网格的单元可以是任何形状。这允许用户对几何复杂度非常高的流体区域进行离散。非结构网格允许非常快速、有时甚至是自动的生成,这对于工业应用来说非常重要,因为在工业应用过程中需要尽可能快速地获得结果。
图1.3a显示了一个二维非结构网格。由于网格寻址不是结构化的,所以仅出于解释网格连通性的目的对单元进行了标记。无序的网格单元使得在特定方向上执行操作变得更加复杂,但无需执行昂贵的额外搜索及在局部重新创建网格方向信息。非结构网格的另一个优点是能够直接对网格进行局部细化,如图1.3b所示。局部细化在控制网格密度方面更为有效,因为它只在需要时提高网格密度。
注:OpenFOAM中的网格连接是完全非结构的。对于简单几何区域,常使用blockMesh以块方式生成网格,但这并不意味着会生成块结构网格。
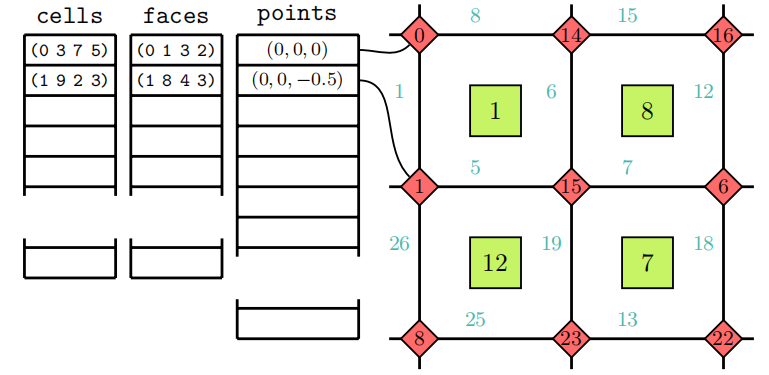
数值算法对网格单元的寻址方式屈居于网格的连接性。OpenFOAM依靠Indirect addressing、Owner-neighbor addressing和boundary mesh addressing来寻址网格单元。
1. Indirect addressing
Indirect addressing(间接寻址)定义了如何从网格节点组装网格,其中网格以全局点列表的形式给出。网格面使用整数标签对全局网格节点列表进行索引。这样在构造网格面时,不需要重复点的坐标,从而能够节省内存,并提高计算效率。因此,每个网格面都是全局网格节点的整数索引列表。网格中的所有网格面都存储在一个全局面列表中(一个索引列表的列表)中,这就是间接寻址这个名称的含义。类似地,网格也被构建为索引列表,用于寻址全局面列表中的面的位置,如图1.5所示。与网格面一样,网格单元也存储在全局(单元)列表中。如图1.5所示的面1就是一个例子,它是由点0和点1以及图中未显示的点3和点2构成的。该面又被用于组装单元1。用于网格面和网格单元的间接寻址可避免在创建网格面或单元的实例时复制网格节点,否则在内存中会存储多个相同网格节点和网格面的副本,这将浪费计算能力,并会使数值和拓扑操作严重复杂化。
2. Owner-neighbor addressing
Owner-neightbor寻址定义哪个网格拥有某个面,哪个网格是该网格面的邻居网格。此外它还优化了对网格面的访问。当使用二阶精度的非结构FVM离散输运方程时,离散由每个网格面上的总和组成,且在每个网格面的中心使用插值。由于相邻网格共享网格面,每个网格面的离散计算会导致在两个网格共享的网格面上执行两次相同的计算。为避免出现这种情况,在网格中引入两个全局列表:face-owner列表和face-neighbor列表。每个网格面最多由两个网格共享。由于网格存储在全局网格列表中,因此它们由其在该列表中的位置索引(cell label)唯一标识。具有较小索引的网格成为与具有较大索引的网格共享的面的owner网格。在图1.6中,面的owner网格用标记,与面相邻但具有较大网格索引的另一个网格称为face-neighbor,其在图1.6中用标记。面区域法线向量的方向如图1.6中的箭头所示。面法向量总是从owner指向neighbor,从索引较小的网格指向索引较大的网格。这样,不是在所有网格单元上离散计算,而是在所有网格面上只计算一次。然后,按照外向法线面积向量的约定,通过离散的微分运算操作将面中心处的贡献加到owner上,并从neighbor中减去。
3、Boundary addressing
Boundary addressing(边界寻址)负责处理边界网格面的寻址问题。根据定义,所有只有一个owner网格且没有neighbor的网格面都是边界面。为提高效率,边界网格面存储在网格面全局列表的末尾,并组合为patch。 将边界网格面分组为边界patch与应用边界条件有关,对于不同的边界面组,边界条件会有所不同。因此,完整的边界网格定义为边界面列表。这允许高效地将边界面定义为全局网格面列表的子集。边界网格的这种定义导致OpenFOAM中依赖于基于网格面的插值实践的所有顶层代码的自动并行化。因为它们只有一个网格owner,所以边界网格的所有法向量都指向计算域的外部。
虽然间接寻址和非结构化网格连接增加了处理复杂几何体和应用局部优化的灵活性,但间接寻址是有代价的。与结构网格代码相比,间接寻址降低了代码的性能。
图1.6显示了面owner-neighbor寻址机制如何对非结构网格的体心值寻址的示意图。为每个网格面定义索引对,该索引对包含与面相邻的网格和的索引及。具有较小网格索引的面相邻网格称为的所有者网格(Owner),具有较大索引的网格称为所谓的相邻网格(Neighbor)。索引标记网格1的边界面,边界面只有一个owner网格:网格1本身。
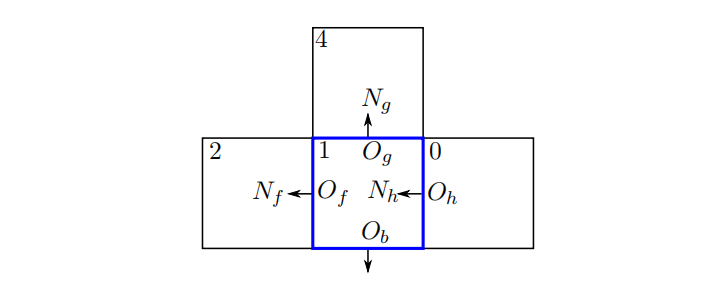
OpenFOAM中的非结构网格也存储了其他的寻址,如单元单元和网格节点。附加寻址可以用来构造不同于非结构FVM的、需要不同网格单元连通性的数值方法。
时间被认为是求解域的附加维度,时间间隔被离散为分区,其中,差值称为时间步长,是前一个时间点,是当前时间点,是下一时间点。
1.3.2 方程离散
一旦求解域被离散为有限体积,就可以对数学模型中微分算子()的项进行近似,将其转化为方程 中的离散微分算子。非结构 FVM 的离散微分算子表示为网格中心平均值(由式 )计算)的线性组合,换句话说,它们是以网格中心值为因变量的线性代数方程组。由于网格 的偏微分方程的离散过程将离散形式的 PDE 表示为其相邻网格中心值的线性组合,因此相邻网格会影响网格 中的解。由于这是针对每个网格 进行的,所以离散得到基于网格 和 的全局代数线性方程组,然后求解 。下一节将介绍如何使用非结构 FVM 方程离散来实现这一点。
非结构化FVM的其他描述可见[文献](6 “F Moukalled, L Mangani, M Darwish, et al. The finite volume
method in computational fluid dynamics. Springer, 2016.”)和[文献](2 “Charles Hirsch. Numerical computation of internal and external flows: The fundamentals of computational fluid dynamics. Elsevier, 2007.”)。OpenFOAM中非结构FVM的公开描述可以在[3](3 “Jasak. “Error Analysis and Estimatino for the Finite Volume Method with Applications to Fluid Flows”. PhD thesis. Imperial College of Science, 1996.”),[5](5 “F. Juretić. “Error Analysis in Finite Volume CFD”. PhD thesis. Imperial College of Science, 2004.”),[12](12 “O. Ubbink. “Numerical prediction of two fluid system with sharp interfaces”. PhD thesis. Imperial College of Science, 1997.”),[9](9 “Henrik Rusche. “Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions”. PhD thesis. Imperial college of Science, Technology and Medicine, London, 2002.”)等文档中找到。
方程 的所有项都需要离散才能得到代数方程。数值方法必须是一致的(见[1](1 “J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3rd rev. ed. Berlin: Springer, 2002.”)):随着网格尺寸的减小,离散(代数)数学模型必须接近精确的数学模型。也就是说,无限细化计算域并在此空间离散上求解离散模型,可以得到由偏微分方程组成的数学模型的解。为了获得离散模型,在网格区域 上对方程 进行积分:
回想一下式 中给出的与 中心相关的二阶精度体积平均值:
1.3.2.1 时间项
利用式 对式 中的时间项进行离散化,并对网格中心值使用速记符号 ,可得到空间二阶精度离散:
然后可以使用有限差分来近似时间项。在OpenFOAM中,可以使用first-order backward Euler(Euler)或second-order backward difference二阶精后向差分(BDS2)格式,即
式中,为新的时间步,为当前时间步,为前一时间步。最后,使用由式(1.11)给出的二阶精度后向差分格式(BDS2),时间项被离散为:
1.3.2.2 散度(对流)项
利用散度定理对方程(1.8)中的进行离散:
方程(1.13)中解域的边界是由线段(几何边)限定的并集面,即有:
式中,为网格域的面的索引。式(1.1.3)可写为:
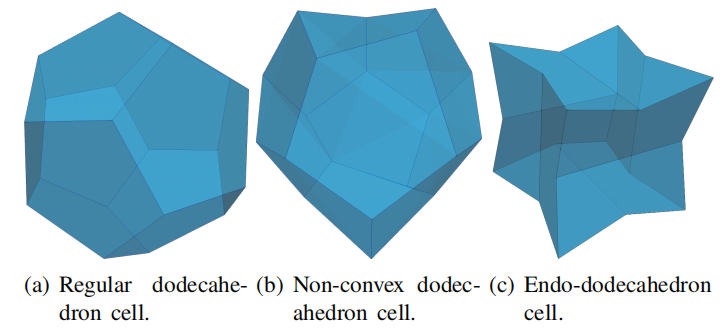
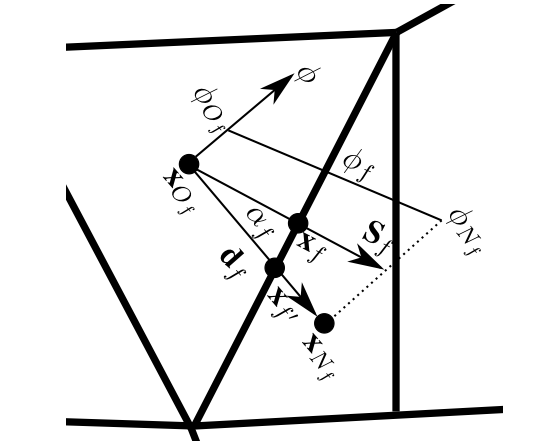
若网格为凸多面体(四面体、立方体、长方体等),则网格的网格面为平面多边形,如上图1.7a中所示的十二面体。或者可以是“广义多面体”:由面围成的非凸体,这些面既可以是非平面,也可以是平面且非凸的面。例如,图1.7b中的非凸十二面体是非凸的,原因很简单,因为它的面不是平面。图1.7c所示的内十二面体是非凸的,因为它的面虽然是平面,但却是非凸的。多面体网格生成算法通常创建非平面多面体,如图1.7b所示。此多面体的面是以直线段(网格边)为边界的非线性直纹曲面。这在图1.7b中的非平面多面体的顶面清晰可见。内十二面体对于多面体网格的生成并不那么重要,尽管理论上它可以出现在十二面体网格中。为了避免在离散过程中引入特殊情况的处理,OpenFOAM中将所有的网格视为广义的多面体。通过使用每个多边形面的质心将面分解成一组三角形来线性化所有的网格面。当网格确实是凸多面体时,这当然不会引入误差。如果是具有非平面面的广义多面体,则使用基于质心的三角剖分对其面进行三角剖分会在方程式(1.15)上引入逼近误差。
为了进一步离散式(1.15),通过应用由式(1.7)给出的平均的2D等效函数,对每个面进行的平均,在面的质心处:
其中,。将方程(1.16)插入式(1.15)可得到:
由等式(1.1)给出的散度项的空间二阶精度离散。在OpenFOAM中,使用所谓的同位离散(collocated discretization):线性代数方程组中的所有因变量都存储在网格中心。因此,使用存储在每个面的两个面相邻网格中心处的值来表示等式(1.17)上的面心平均值。
注:非结构FVM中,面心平均值相当于体心值,具有二阶精度。
应用于正交三角形网格的中心差分插值格式如下图所示。
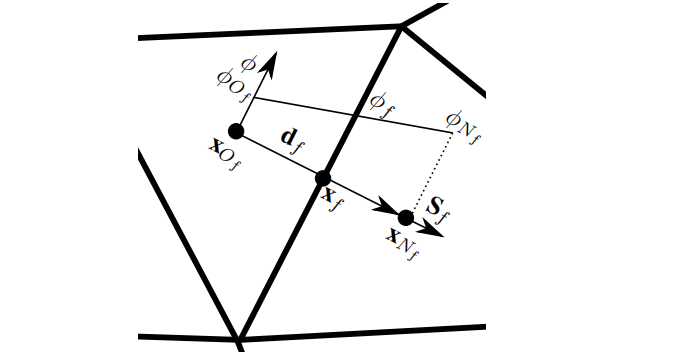
考虑图1.8所示的2D三角形网格上的面f及其两个相邻的所有者网格和相邻网格,如果以面心值使用线性插值(中心差分格式,CDS)表示的,就有:
式中,;OpenFOAM中所谓的delta系数;为通过CDS格式计算的线性面系数:
面系数 , 也可以使用迎风格式进行计算,对于对流项,可以使用存储在上游网格体心上的值来定义:
式中,为出的标量体积通量:
若指定了速度,则其不是方程(1.1)中的因变量,并且其在方程(1.17)中的表达方式与完全相同,使用线性插值(CDS)或方程(1.19)中面相邻值的其他组合。
将面心平均值计算为来自相邻网格的单元中心值(例如通过CDS方程(1.18))以及来自方程(1.22)的标量体积通量的组合,可以得到离散散度算子为:
式中,为属于网格的owner面的索引集。
到目前为止,没有对网格边界的法向量的方向(即网格的网格面的法向面积向量的方向)作出任何假设或离散。然而,OpenFOAM不会使用网格所有面上的和(索引集)来离散方程(1.1)(方程(1.8))中的散度/扩散微分算子项,也不会在OpenFOAM中为每个网格一致地确定其边界的法向量方向(仅向外或仅向内)。对于每个网格面中心,定义唯一的向量。这妨碍了法线的一致性,因为对于与面相邻的网格,必须向内。
离散散度算子在OpenFOAM中通过使用owner-neighbor寻址实现。向量为式中从owner单元指向neighbor单元的面法向向量,这是OpenFOAM中非结构FVM的一个非常重要的实现。
散度定理假设方程 (1.13) 中边界 的法线方向一致:法线 可以相对于单元 向外或向内,并且在OpenFOAM中使用法向方向向外的约定。等式 (1.23) 对散度项的离散化导致网格的所有面的总和。如果要对每个网格执行离散化,则强制法线方向的一致性会很复杂。例如,对于图 1.6 中的网格 1,由于所有者-邻居寻址,单个面区域法线向量方向向内。以任何其他方式定义唯一的法线向量 Sf 仍会使该向量从一个网格指向另一个网格,有效地指向其中一个网格。onwer-neightbor寻址用于第 1.3.2 节中介绍的域离散化,因为它根据面相邻网格的索引唯一地确定法向方向:owner网格的索引小于neighbor网格。
所以问题是:如果网格(图 1.6 中的网格 1)的一些面朝外而有些面向内,如何进行方程(1.23)给出的散度项的离散化?
由于向量总是从具有较低索引的网格 (face-owner, owner-cell, owner) 指向具有较高索引的网格 (face-neighbor, neighbor-cell, neighbor),因此对r.h.s.总和的贡献被添加到owner面,并从面 的neighbor中减去。为了实现这一点,引入了两个索引集:owner(owner-cell ) 和neighbor(neighbor-cell)索引集,即
由等式(1.24)和(1.25)给出的索引集O、N分别包含网格中每个面的所有者和邻居单元的标签,而不是像等式(1.23)中的索引集Fc那样包含单元的每个面的所有者和邻居单元的标签。这使得即使当单元的法向量SF不都指向外部或内部时,也可以执行与等式(1.23)中相同的计算。
对于所有,有:
其中F为网格中所有面的索引几何,为由方程(1.24)给出的面owner单元从O中得到的索引,为由方程(1.25)给出的面相邻单元n的索引,为由方程(1.23)给出的离散散度算子。
注:方程(1.23)对散度算子的离散有助于理解非结构化有限体积法,而OpenFoam中的实际计算则是用方程(1.26)进行的。
注:可以使用FVMesh类的owner()和neighbour()成员函数从网格访问所有者和邻居索引集。
如第1.3.1节所述,并在单元格1的图1.6中所示,边界面只有一个所有者-单元格。 因为这个面没有邻居单元,所以在等式(1.26)中它不会有贡献。 为了避免检查面是否属于网格边界,边界面(图1.6中的B面)在OpenFoam中与内部面分开存储。
1.3.2.3 Laplace(扩散)项
方程(1.1)中的拉普拉斯(扩散)项与散度(对流)项相似地离散化。 离散从上的积分和散度定理的应用开始,使用速记符号,可以得到:
其中空间二阶精度误差项是由方程(1.16)给出的面内平均产生的。
拉普拉斯项离散的下一个步骤是梯度的离散。 方程(1.27)中的面心梯度不是从面相邻网格中心梯度中插值得到的。取而代之的是,泰勒级数从面中心到owner,以及到neighbor网格中心都被使用。 为了简化表达式,引入了以下速记表示法。 对于面心值,使用(等价于),此外还使用向量的张量积表示法:
利用这种表示法,从面心、面owner和neighbor分别给出泰勒级数为:
从式(1.29)减去式(1.28)得到:
在等距网格上,类似于图1.8中所示的网格,面中心将向量分解成两个相等的部分,这样
将方程(1.31)代入方程(1.30)中,乘以,除以,就可以消除方程(1.30)中的二阶项,即:
这导致面心梯度的最终离散为:
方程(1.33)只在满足方程(1.31)的等距网格上,并且对于可展开为泰勒级数的足够规则的,证明了面心梯度在项中的二阶精度,但只有在满足方程(1.33)的等距网格上才具有二阶精度。 如果方程(1.31)不成立,则方程(1.33)中的最大误差项包含来自方程(1.30)的贡献,这使得离散具有一阶精度。
在预计φ发生强烈变化的区域,宽高比应为理想的0.5,因为这样方程(1.31)成立,并实现了方程(1.33)的二阶精度离散。 在不足够小且对求解的二阶收敛几乎没有影响的情况下,可以使用更强的网格分级。
考虑图1.9:在垂直方向上变化很大,边界层捕捉到了的垂直变化。 然而,边界层在停止之前结束时变化很大,并且由于长宽比不等于0.5,在用表示的面上的梯度离散引入了一阶误差项。 另一方面,在图1.9中没有任何水平变化,因此不等于0.5的纵横比实际上对这些面的求解精度没有影响。
利用方程(1.33)对进行二阶精度离散,通过将方程(1.33)代入方程(1.27)来确定Laplace项的离散,得到Laplace(扩散)项的二阶精确FVM离散:
如果和共线(),或者换句话说,如果网格是正交的,方程(1.34)对Laplace项的离散可以进一步简化,如
图1.10中显示了一个非正交网格:在一个非正交网格中,在面处,向量不共线,形成一个所谓的非正交角。 非正交性在方程(1.35)中引入了一个误差,基于高斯散度定理,利用网格中心梯度的离散来校正这个误差。 网格质心处的梯度可以离散为
二阶精度由方程(1.16)中的面心平均和方程(1.18)中的线性插值给出。 在网格质心处以这种方式离散的梯度用表示。 如果方程(1.36)与方程(1.18)在面中心处线性插值,即
由于线性插值是有界的,面心梯度保持了方程(1.36)给出的owner及neighbor梯度的二阶精度,这意味着它保持了和网格的误差的界。 在方程(1.36)中,二阶精度项简化为:实际上,在一般非结构网格上,该表达式更为复杂。 该误差可以用最大误差来粗略估计,如及,其中是所有面点的集合。 最后,在方程(1.31)给出的条件下,即使,以网格为中心的高斯梯度的线性插值仍保持二阶精度。
用方程(1.36)近似的面心梯度在方程(1.27)中不用于拉普拉斯项的离散,因为方程(1.37)会引起所谓的棋盘网格。 棋盘网格是指在某些情况下,由于方程式(1.37)中存在的人为抵消,离散无法计算。 作为一个最简单的例子,考虑五个用(0,1,2,3,4)标记的一维有限体积网格,它们之间有一个单位距离,在它们的网格中心有(50,100,50,100,50)的分布。 如果使用公式(1.18)和(1.36)计算以网格为中心的梯度及,以及基于owner-neighbor寻址的法向量定向(分别为),则所得梯度为和。 这些假零点,通过方程(1.37)进一步插值以计算面心梯度及保持零值。
或者,如果用公式(1.37)计算,则有,同样适用于。 这个例子显然是人为的,但它表明离散忽略了两个相邻网格之间求解的振荡,这种振荡虽然不像这个例子中那样有规律,但实际上可以是求解的一部分。 这种振荡的一个例子是压力中由一系列小的(未解析的)涡旋引起的振荡。
方程(1.37)不使用面心梯度,因为它会导致棋盘式。
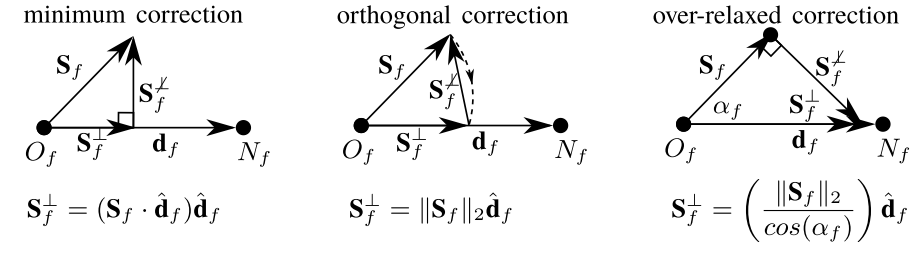
由方程(1.37)给出的线性插值面心梯度可以用来校正方程(1.35)中的非正交性。 通常用于表面积法向量分解的方法有三种:最小校正法、正交校正法和过松弛校正法。 三种方法都将面积法向量分解为与共线的正交部分和非正交部分,
这样:
图1.11给出了不同的的计算方法,并根据方程(1.39)计算了\mathbf{S}_f^\cancel{\perp}。 用方程(1.33)计算方程(1.40)中的梯度的正交贡献,该方程包含两个面相邻网格的平均值,并采用隐式离散化。非正交项贡献(\nabla \phi)_f^\cancel{\perp}采用显式离散。
对方程(1.40)中(\nabla \phi)_f^\cancel{\perp}的显式离散结果为:
这是不成立的,因为正交和非正交贡献是在不同的时间步长上评估的。 为了修正方程(1.40)中和之间的差异,在OpenFoam中使用在每个时间步长内附加固定数目的附加迭代进行非正交修正,即
希望经过次迭代后,。 非正交校正的迭代在压力-速度耦合算法中起着至关重要的作用,其中拉普拉斯算子用于压力的泊松方程。 这就是为什么OpenFoam中的pressure velocity耦合算法的配置文件有一个适当的条目。
注:
- 在 OpenFoam 中,用于压力泊松方程的非正交性校正的迭代次数 可以在 System/FVSolution 配置文件中设置。
- CheckMesh应用程序报告了非结构OpenFoam网格中的非正交角信息。
- 在一般情况下,如果网格是非正交的,也是非等距的,此时方程(1.31)不成立,在面心处的梯度近似变成一阶精度。
通常,网格非正交性将和之间的交点(图1.10中的点)从面中心移开,用于方程(1.16)中的平均。 方程(1.16)期望面平均值与面中心相关联,以确保二阶精度,并且由于是插值实际发生的地方,因此引入了所谓的网格偏斜误差。
注:如果方程(1.16)中用于面上平均的面中心不对应于交点,则会引入网格偏度误差。
在科学文献中提出了不同的解决偏斜误差的方法,但目前在OpenFoam中没有任何偏斜校正方法是可用的,因此这里不详细讨论偏斜误差。 关于非结构FVM的非正交性和偏度误差的附加信息可以在[3,5,6]中找到。
1.3.2.4 时间离散
时间离散结合了迄今为止所描述的时间、对流(散度)和扩散(拉普拉斯)项的离散。 使用到目前为止描述的离散化算子重组离散化标量输运方程(1.1),我们可以写
用泰勒级数对进行时间展开,以为时间步长,得到:
且有:
由方程(1.44)和方程(1.46)给出的离散化是等价的,并且具有同等的一阶精度。 然而,OpenFOAM使用方程(1.46)给出的隐式欧拉离散,因为它对于初始条件光滑的线性方程组是无条件稳定的。
将方程(1.46)插入方程(1.42)中,得到了标量输运方程(1.1)的离散,采用了常用的隐式欧拉格式,该格式在时间上具有一阶精度,在空间上具有二阶精度:
其中源项要么在旧的时间步处求值,要么在和时间处使用线性外推。 关于源项线性化的附加信息可以在[7]中找到。 或者,将方程(1.44)插入方程(1.42)并将所得方程与方程(1.47)求和,得到Crank-Nicolson格式:
这在时间上也是二阶精度,因为项和分别在方程(1.44)和方程(1.46)的求和中抵消,留下作为前导截断项。 验证这一点留给读者做一个简短的练习。
OpenFOAM中应用CreakNicolson格式,可以在system/fvSchemes文件中设置:
ddtSchemes
{
default
CrankNicolson 0.5;
}
在OpenFOAM中,Crank-Nicolson格式中的系数0.5是通过将隐式和显式项组合在一起而变的,即:
当时,从方程(1.49)恢复方程(1.48)。 如果用方程(1.46)表示得到方程(1.47)给出的一阶欧拉隐式方法。
在仿真案例中,在仿真文件夹的System/fvSchemes字典中选择时间积分格式,如清单所示,其中使用。 当然,方程(1.49)中的源项是的线性化函数,这保证了一个线性代数系统是由方程离散得到的,可以用线性求解器求解。
ddtSchemes
{
default
CrankNicolson 0.5;
}
1.3.2.5 线性代数方程组
用方程离散法构造了一个线性代数方程组,求解了网格中每个网格中的。 例如,考虑由方程(1.48)在正交网格上给出的离散。 项和将分别依赖于方程(1.35)和方程(1.23),从时间步长中,将来自网格C的面的值引入方程(1.48)。 其他项,如只包含当前和新时间步长的值。 从网格C和它的面邻居集合中分离贡献,得到一个线性代数方程,通常写为
隐式离散,如公式(1.48)所示,为网格中的每生成一个线性代数方程(1.50)。 方程式1.50是相互耦合的,因为在方程式中,对于每一个单元,都有来自相邻网格的贡献。 然而,由于贡献仅来自于与单元共用一个面的相邻单元,方程组将只有几个非零系数,由此得到的线性系统将是稀疏的。 求解稀疏线性代数系统的结果是对于新的时间步长计算网格中的每一个值,
1.3.2.6 边界条件
当一个面心值属于作为网格边界一部分的单元面时,在离散中需要边界条件。 所谓的边界面不具有相邻单元格,相邻单元格的值参与离散。 相反,定义的内容通常是:
- 值由Dirichlet或固定值边界条件指定
- 梯度由Neumann边界条件指定
- 或者一个值和梯度的线性组合是由混合边界条件或Robin边界条件指定
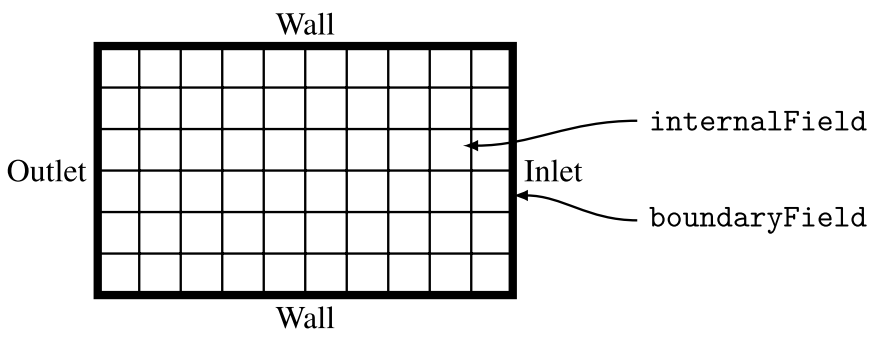
无论离散的隐式或显式性质、用于的插值格式或用于的梯度离散格式,边界条件在边界面上都是必要的。 图1.12中的粗线突出了边界面。
例如,用方程(1.48)组合线性代数方程方程(1.50),离散化算子所用的求和在某些单元中会遇到边界面。 让我们考虑对流算子,假设这样的边界面用标记,那么显然,离散对流项中的和应该加上。 对于内部面,该值将在与面b相邻的网格的以网格为中心的值之间插值。 但是,边界面旁边只有一个网格,根据定义,这个网格是那个面的owner。
对于FixedValue边界条件,过程很简单: 边界条件指定了属性的取值,速度的取值。这对于定值边界条件就足够了,但这使边界条件的实现变得非常复杂。 网格中的绝大多数面是内部面,而不是边界面。 因此,将内部面和边界面以某种方式混合在一起并加以分类是没有意义的,这样离散就可以“询问每一个面”它是否属于边界,以及另外为这个面规定了哪一个边界条件。 为了避免这一复杂情况,网格的面被分成内部面和边界面。 在OpenFOAM中,边界面被进一步分组为边界Patch:应用相同边界条件的边界网格子集。 这是有意义的,因为模拟过程通常有暴露在不同条件下的表面。 以传热为例:有些表面可以被隔离,有些表面可以通过流动的空气或液体喷雾冷却,有些表面将邻近由不同材料制成的物体。 因此,如图1.12所示,OpenFOAM中的物理场被分为内部(以细胞为中心的)物理场和边界面为中心的物理场,分为与特定边界斑块(边界条件)相对应的斑块物理场。 由于离散化算子中求和的方法可以分别应用于区域的内部和边界,因此,将面和边界分别划分为内部和边界块以及物理场,从而大大简化了OpenFOAM中的离散。
另一个边界条件是Neumann或“自然”边界条件,它规定区域边界处的性质梯度为零:
因此,在零梯度边界条件下,边界面上的值取自网格中心的值,即
对于边界面b上的零梯度边界条件,对代数方程方程(1.50)的边界贡献将以新时间步长中的单元值旁边的系数结束:方程(1.50)中的。 换句话说,零梯度边界条件将影响边界块下一个单元的线性代数方程组的对角线系数。 在OpenFOAM中实现了各种边界条件,它们要么指定了边界值,要么指定了梯度,或者指定了两者的组合。
1.3.2.7 解线性代数方程组
求解由非结构化FVM生成的线性代数方程组(线性方程组)通常需要大量的计算工作,因为它的大小为,其中是网格中的网格数,d是空间维度。 因此,方程(1.50)中旁边的系数是稀疏矩阵中的系数。 OpenFOAM使用一种特定的矩阵表示格式,以及一组与OpenFoam矩阵格式紧密耦合的线性求解器。 这里没有涉及这个主题,相反,读者可以参考[6,第10章]了解关于OpenFOAM矩阵格式和线性求解器的详细信息。 请注意,除了许多教程中的配置之外,很少需要对OpenFOAM中的线性求解器配置进行重大调整或修改。 文献[11]提供了共轭梯度线性求解器的一个信息和直观的推导。 关于稀疏线性系统的迭代求解方法的详细背景知识可在[10]中获得。