动态网格类的设计因每个特定动态网格的功能而异。本章简要概述了OpenFOAM中动态网格的功能和设计，包括网格运动和网格拓扑更改。

13.1.1 网格运动

OpenFOAM中实现的网格运动操作主要有两种类型：实体网格运动和网格变形。

顾名思义，实体运动会置换网格点，同时保持其相对位置。实体网格运动涉及网格的平移和旋转或两者的组合，并且可以将其规定为或计算为对实体动力学建模的常微分方程的解。

与网格运动相反，网格变形将位移从网格边界不均匀地分布到求解域的内部。位移分布采用不同的方法：代数插值或求解点位移或速度的输运（通常是拉普拉斯）方程。

13.1.1.1 实体网格运动

实体网格运动如图13.1所示。在OpenFOAM中，实体运动由各种类定义，所有类都从它们的公共基础派生：实体运动函数。motion函数返回描述物体运动的七元数。此运动是平移向量和旋转四元数的组合。七元数使用相同的向量转换来置换每个网格点。关于四元数的更多信息可以在[2]的书中找到。

图13.1 填充主体会受到实体主体运动的影响，因此网格点不会相对于彼此移动

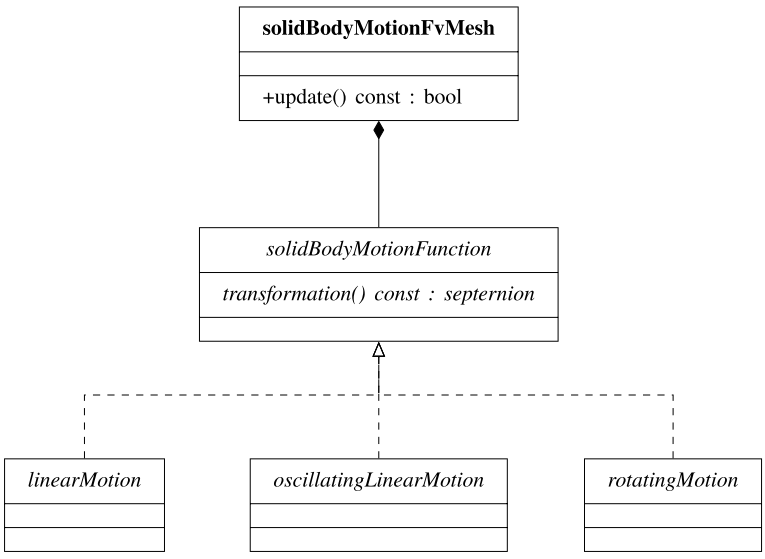
从抽象基类solidBodyMotionFunction派生的类定义存在的运动类型。从简单的运动（如linearMotion和rotatingMotion）到复杂的运动（如tabulatedMotion）(SDA用于船舶耐波性调查）。从图13.1中的UML图中可以看出，solidBodyMotionFunction定义了虚拟方法转换，该转换又由每个派生类实现。它计算用于在初始位置与当前时间的位置之间变换网格点的分隔数，并表示平移与旋转。

转换函数封装在一个类中，该类支持运行时选择和重用。从solidBodyMotionFunction派生的任何类都不会更改网格点的位置，它们只提供转换。

执行实际实体网格运动的动态网格类名为solidBodyMotionFvMesh，它继承自dynamicFvMesh。图13.2中的类图显示了solidBodyMotionFvMesh和solidBodyMotionFunction之间的关系。使用solidBodyMotionFvMesh类的策略模式（[1]）实现变换函数。因此，实体主体运动功能可由其他数据库零件作为独立图元重复使用。要计算实体运动，类和实体网格运动之间的关系必须未知。此外，solidBodyMotionFunction是使用Strategy模式设计的，允许轻松添加其他函数。只需从solidBody MotionFunction继承，即可使新函数在运行时可选。

图13.2 solidBodyMotionFvMesh和solidBodyMotionFunction类图

策略模式：在类层次结构中封装各种算法，在客户端（用户）类中组合它们，并使它们在运行时都是可选择的。

另一方面，如果将solidBodyMotionFunction实现为solidBodyMotionFvMesh类中的Template Method模式，则添加另一个网格运动函数将导致多一个动态网格类。模板方法模式应用程序的一个示例是dynamicFvMesh类和派生的动态网格类，它们实现了更新算法。

solidBodyMotionFunction类层次结构的设计是SRP设计原则的一个很好的示例：即使运动函数相当简单，它们也被封装为具有单个简单责任的单独类。运动函数只与计算变换有关，不涉及其他任何内容。此外，运动功能通常可以被组合：例如，可以是，具有恒定旋转的振荡线性运动。在这种情况下，TemplateMethod模式会崩溃，因为它依赖于对动态网格类使用多个继承。

模板方法模式：虚函数用于实现算法，并且（基）类可以提供默认算法实现。因此，衍生类别会实作各种不同的替代算法，在阶层架构中产生每个算法的分支。

solidBodyMotion动态网格使用由用户选定的solidBodyMotionFunction定义的同一分隔数变换网格的所有点或特定部件（即cellZone）。如果未指定cellZone，则使用相同的分隔数移动所有网格点;因此实现了匀速运动。如果在字典中指定了cellZone，则只有cellZone中单元格的点会相应地移动。当物体在转子-定子配置中旋转时，使用滑动界面（AMI/GGI），这就很方便了。除了solidBodyMotionFvMesh之外，还有multiSolidBodyMotionFvMesh，它的功能基本上与solidBodyMotionFvMesh相同，但允许多个运动叠加或作用于不同的单元区域。后者对于两个转子旋转、使用不同单元区和AMI/GGI接口的应用非常重要。使用fvMesh::movePoints将运动本身直接应用于所有相关网格点，因此无需求解额外的方程，这使其成为一种相当快速的方法。

基于网格区域的网格点选择可用于涉及滑动界面的转子-定子网格运动配置。

12.1.1.2 网格变形

网格变形会在网格点之间引入不同的相对运动，从而使边、面和单元变形。网格变形导致的高度扭曲可能会破坏网格的质量。

注：网格质量取决于选择方程离散化的数值方法。有限体积法,最重要的两个mesh-related离散化错误non-orthogonality和偏态误差([3],[6])。

为确保高网格质量，通常仅对网格的一小部分子区域进行强烈变形。相比之下，网格的其余部分的变形保持尽可能低，例如，在网格边界附近。另外，网格变形可以看作是一个优化问题，其中网格的质量表示一个域-全局优化的标量函数。如果将最强位移应用于网格边界的特定部分，则问题仍然是如何将位移传播到网格的其余部分，同时使网格运动不感兴趣的区域中的变形保持最小。在整个求解域中传播网格运动的两种最主要的方法是代数位移插值法和位移的拉普拉斯方程求解法。

位移从网格边界到网格的扩散使用拉普拉斯方程建模： $\nabla \cdot (γ \nabla d) = 0 (13.1)$ 其中 $γ$ 是位移扩散系数， $d$ 是点位移场。扩散系数 $γ$ 在空间上随点 $x$ 与网格边界之间的距离而变化，即： $γ = γ (r) (13.2)$ 在方程（13.2）中， $r$ 是网格点和网格边界之间的距离，并且以使得系数随着与边界的距离而减小的方式规定系数函数。方程（13.1）使用OpenFOAM中的FVM近似。在这种情况下，求解的场以单元为中心，边界场存储在面中心。为了使用FVM计算网格点（单元角点）中的位移，需要执行从单元中心值到网格点的插值。或者，在foam-extend中，方程13.1的解可以使用有限元法（FEM）来近似。

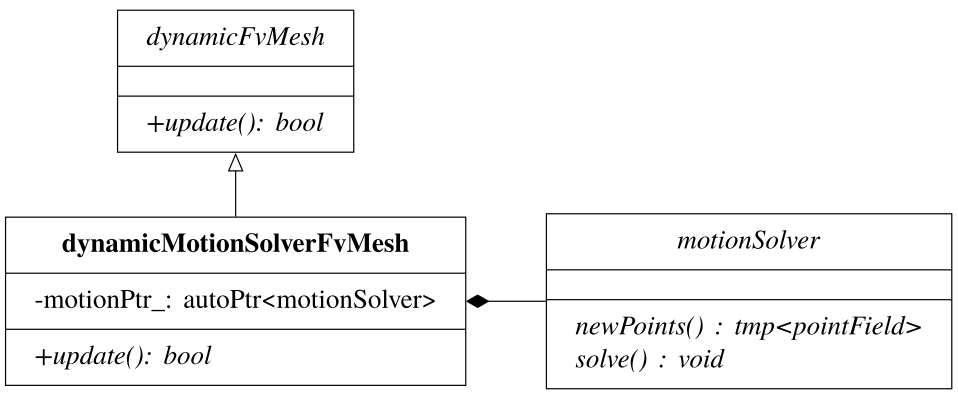
涉及拉普拉斯方程解的网格变形由dynamicMotionSolverFvMesh实现，如图13.3所示。

图13.3 网格运动由dynamicMotionSolverFvMesh类实现

运动物体的运动由其边界描述，这通过将运动边界条件分配给物体边界网格的相应部分来完成。运动边界条件可以作为速度或位移的显式函数给出，或者可以基于外部数据计算。例如，数据驱动的网格运动边界条件可以使用计算的数据来求解由在物体边界上积分的流体力驱动的固体物体运动。

当物体相对于大的解域仅轻微移动时，外部面片的位移通常被设置为固定的零值位移边界条件，该条件基本上固定了空间中这些域边界上的所有点。

一旦用位移（速度）场的边界条件规定了边界运动，运动解算器就承担了在解域内求解运动场的责任。motionSolver在dynamicMotionSolverFvMesh中合成并实现为抽象基类以允许不同的方法来求解运动场（例如，有限体积方程解或位移代数插值）。运动解算器的概念是生成新网格点所必需的，除此之外没有其他要求-网格点的运动随后被进一步委托给父类fvMeshClass：

bool Foam::dynamicMotionSolverFvMesh::update()
{
    fvMesh::movePoints(motionPtr_-> newPoints());
    if (foundObject<volVectorField> ("U"))
    {
        volVectorField&amp; U =
        const_cast<volVectorField&amp;> (lookupObject<volVectorField> ("U"));
        U.correctBoundaryConditions();
    }
    return true;
}

而运动解算器（motionPtr_）只需要使用newPoints成员函数生成新网格点：

Foam::tmp<Foam::pointField>  Foam::motionSolver::newPoints()
{
    solve();
    return curPoints();
}

调用newPoints会导致修改网面点的网面变形近似。通过求解实现的求解过程将根据使用插值或拉普拉斯方程来传播位移而有所不同。可以使用不同的运动解算器，但描述所有这些解算器超出了范围。

选择位移场的有限体积求解器作为示例，即displacementLaplacianFvMotionSolver。与拉普拉斯有限体积网格运动解算器交互的两个最重要的类如图13.4所示。

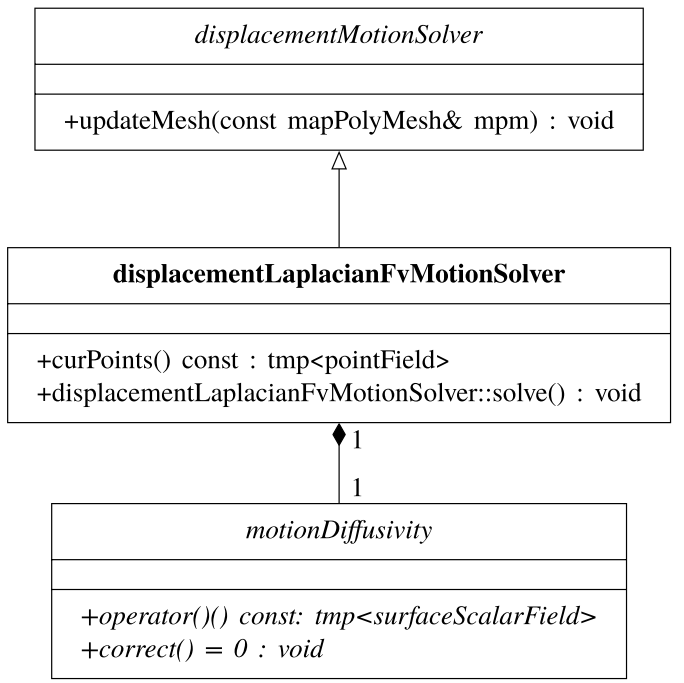
图13.4 基于拉普拉斯有限体积的运动求解器类图

displacementMotionSolver封装网格变形所需的置换场，并提供对其他置换解算器的字段访问。motionDiffusivity是用于计算可变扩散系数的策略（即OpenFOAM模型），由等式13.2给出。然后，该空间可变场可用于缩放位移，该位移通过插值或作为扩散方程13.1中的系数传播到网格的内部。网格运动扩散率的新函数可以很容易地开发出来：从motionDiffusivity继承并将其自身注册到RTS表的类在网格运动框架中自动变为可用。

注：尽管我们在本节中省略了OpenFOAM中网格运动的一些细节，但可用信息应足以理解和扩展网格运动。

由displacementLaplacianFvMotionSolver实现的Laplacian有限体积网格运动解算器（如图13.4所示）在解算成员函数中解算单元中心位移场的扩散方程：

diffusivityPtr_-> correct();
pointDisplacement_.boundaryField().updateCoeffs();
Foam::solve
(
    fvm::laplacian
    (
        diffusivityPtr_-> operator()(),
        cellDisplacement_,
        "laplacian(diffusivity,cellDisplacement)"
    )
);

然后使用反距离加权（IDW）插值法将点位移从单元中心插值到curPoints成员函数内的单元角点（网格点）：

volPointInterpolation::New(fvMesh_).interpolate
(
    cellDisplacement_,
    pointDisplacement_
);

注：每次执行curPoints时（使用基于FVM的运动解算器变形网格时），都会分配一个新的反距离权重插值对象。

创建一个新的IDW插值对象每个时间步是必要的距离反比插值权重变化之间存在相对位移网格点。

13.1.2 拓扑变化

改变网格拓扑包括修改其拓扑信息：添加和删除网格元素（单元、面、边、点）和更新描述网格元素之间相互连接的所有数据结构（例如，边-单元连接列表）。在网格中应用拓扑变化通常是通过在存在大梯度的区域中提高精度或通过对模拟区域的形状和大小经历极端变化的动力系统进行建模来实现的。网格变形可能会导致网格质量的严重下降，因为网格面之间的夹角和相邻网格尺寸的比例可以被严重改变。严重的网格变形导致非结构化FVM的精度损失，因为单元以引入插值、非正交和偏斜误差的方式发生畸变。网格变形可以与网格拓扑变化耦合以保持精度，从而产生更精确和高效的动态网格引擎。

OpenFOAM中的拓扑变化是以单独的操作来实现的，在设计动态网格类时可以将其凝聚起来。处理网格拓扑变化的动态网格通常比网格运动类更专业化，因为拓扑变化通常更复杂。其复杂性在于添加和删除网格单元，改变它们的连通性，并更新场值以解释拓扑变化。 dynamicFVMesh库位于 $FO A M_{S} RC / d y nami c F V M es h 中，包含通用拓扑更改器，如 d y nami c R e f in e f V M es h 。该动态网格基于细化准则（例如，压力梯度）的值区间实现六面体网格的动态和局部细化。用户定义细化标准值区间，并且包含位于用户指定区间内的场值的单元格被动态细化，而那些存储该区间外的值的单元格被未细化。使用不同的物理场作为细化标准也是可能的。例如，细化标准可以使用在用户开发的函数对象中的仿真期间计算的更复杂的细化模型。更专业的拓扑更改器可在下面的路径中找到： ‘‘‘ ba s h$ FOAM_SRC/topoChangerFvMesh


以移动的ConeTopoFvMesh为例：它对气缸内运动活塞的动态模拟进行建模。网格沿x轴方向移动面片（网格边界的一部分）。它在网格高度变形的区域中添加和移除细胞层，以保持高网格质量。在OpenFOAM中开发这种专门的动态网格的能力是抽象级别分离的结果。单个拓扑操作在较低的抽象级别上，并且它们的聚集导致在较高的抽象级别上将单元层添加到网格的操作。

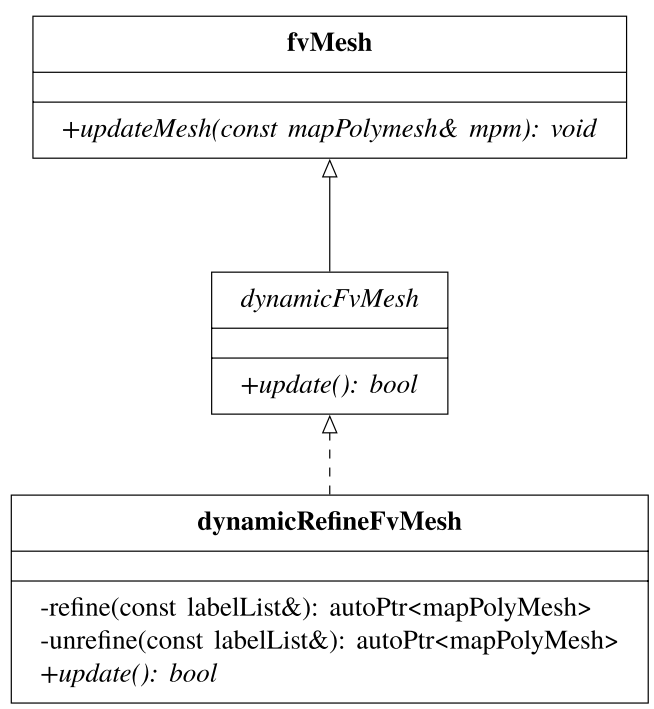
图13.5显示了dynamicRefineFvMesh类的重要类关系。与其他动态网格类一样，它实现了update成员函数以符合dynamicFvMesh接口。网格细化操作涉及单元的细化（分割）和取消细化（合并），这取决于上述细化标准。这两个操作分别由两个私有成员函数refine和unrefine实现。每次执行这两个操作中的任何一个时，dynamicRefineFvMesh类都会与父fvMesh类协作，以便更新拓扑操作的物理场。

![图13.5 由dynamicRefineFvMesh类实现的网格细化](https://faee0-1253397841.cos.ap-chengdu.myqcloud.com/wizimg/202212041633888.png)

在算法2中，显示了网格细化/取消细化的算法，具有降低的细节水平。Mes细化和取消细化生成拓扑图：将修改的网格元素与原始网格相关联的数据。分割立方体单元的网格面会在OpenFOAM中生成多面体单元：这些单元仍然是立方体的，但是具有多于六个面。

```c++
Read the control dictionary for the dynamicRefineFvMesh.
if not first time step then
    Look up the refinement criterion field.
    if number of mesh cells < maxCells then
        Select cells to be refined (refineCells).
        Add cells from the refinement layer and protected cells to refineCells.
            if cells to be refined >  0 then
                refinementMap = refine(cellsToBeRefined)
                update refineCell (refinementMap)
                updateMesh (refinementMap)
                mark the mesh as changed
            end if
    end if
    select unrefinement points
    if number of unrefinement points >  0 then
        refinementMap = unrefine (unrefinement points)
        updateMesh (refinementMap)
        mark the mesh as changed
    end if
end if

注意：OpenFOAM中六面体非结构网格的自适应细化不是基于八叉树数据结构的。网格拓扑被直接改变并存储在新的网格中，使得现有的离散算子和方案能够在拓扑修改的网格上应用。

只要两个相邻单元共享通过分割原始面生成的相同数量的子面，网格的所有者-邻居间接寻址（第1章）将在不修改的情况下工作。然而，重要的是要注意，这种分割引入了非正交性、纵横比和偏斜度误差。因此，通常提供精制细胞的附加层：精细化细胞层的边界应当位于具有小梯度的区域中，在该区域中，高精度不像在精细化网格层内那样重要。

dynamicRefinefVMesh和fvMesh之间的协作是通过调用fvMesh::updateMesh成员函数实现的。物理场的映射可能是一个复杂的算法来实现。当实现一个新的拓扑变化类时，通过遵循图13.5中所示的类关系，可以更容易地重用该算法