1 案例描述
本案例为文丘里管流动的不可压缩流体数值模拟,采用 OpenFOAM 13 版本进行计算。该案例模拟了流体通过文丘里管时的流动特性,可以用于研究管道收缩和扩张段的速度分布、压力变化以及流动特性。
求解器类型:采用通用不可压缩流动求解器 incompressibleFluid
案例基本信息:
-
定常流动(Steady-state) -
不可压缩流体 -
层流流动 -
三维轴对称模型
2 案例几何与网格
2.1 几何尺寸
几何模型如图所示。

文丘里管几何参数:
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2 网格基本信息
案例采用 blockMesh 生成结构化六面体网格。
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
生成的网格如下图所示。

2.3 边界定义
计算区域中包含的边界信息如下所示。
|
|
|
|
|
|---|---|---|---|
| inlet |
|
|
|
| outlet |
|
|
|
| walls |
|
|
|
2.4 网格特征
-
网格类型:采用结构化六面体网格 -
网格生成:使用 blockMesh 工具生成
-
网格分级:径向方向采用分级系数 0.5 进行网格加密 -
对称性:利用轴对称特性,采用四分之一圆截面
3 物理模型
3.1 流动模型
|
|
|
|
|---|---|---|
|
|
|
|
3.2 材料属性
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
3.3 初始流场条件
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
3.4 入口流动条件
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
4 边界条件
4.1 速度场边界条件
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2 压力场边界条件
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 求解控制参数
5.1 时间控制
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.2 输出控制
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.3 离散格式
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.4 线性求解器设置
|
|
|
|
|
|
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
5.5 PIMPLE 算法参数
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.6 松弛因子
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
6 案例后处理
本案例配置了丰富的后处理操作,包括探针监测、速度剖面图和残差监测。
6.1 探针监测
在两个位置设置探针监测压力场:
-
探针1:位置 (0.05, 0.05, 0) - 入口过渡段 -
探针2:位置 (0.25, 0.025, 0) - 喉部段
6.2 速度剖面图
在6个截面位置生成速度分布图:
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
每个剖面沿径向方向(y轴)从 -0.051 m 到 0.051 m 采样速度分量。
7 案例运行方式
7.1 串行计算
采用下面的命令可以进行串行计算:
cd venturiTube
blockMesh
createZones
foamRun
./createGraphs
7.2 并行计算
可以修改 system/decomposeParDict 文件后运行并行计算:
cd venturiTube
blockMesh
createZones
decomposePar
mpirun -np 4 foamRun
reconstructPar
./createGraphs
8 关键物理参数总结
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 计算结果
计算得到的速度剖面图显示了文丘里管内不同截面的速度分布特征:
-
入口段(graphA, graphB):速度分布较为均匀,接近抛物线分布 -
过渡段(graphC):速度开始加速,中心区域速度增大 -
喉部(graphD):速度达到最大值,由于截面收缩,流速显著增加 -
扩张段(graphE):速度开始减速,压力恢复 -
出口段(graphF):速度分布逐渐恢复到接近入口状态
后处理脚本生成的 velocityProfiles.png 图像直观地展示了速度分布沿管道的变化,以及速度分布与几何形状的对应关系。
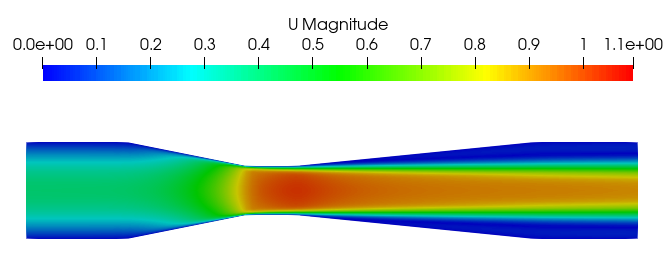
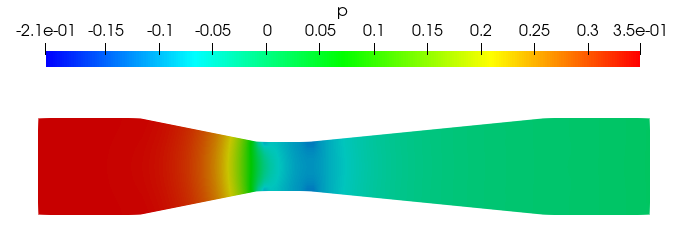
(完)

本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册