
欢迎来到《基于物理的深度学习书籍》(v0.2)! 👋
简要说明:本文档包含在物理模拟背景下与深度学习相关的实用而全面的介绍。所有主题都尽可能以 Jupyter 笔记本的形式附带实践代码示例,以便快速入门。除了标准的数据监督学习外,我们还将研究物理损失约束、与可微分模拟更紧密耦合的学习算法、为物理问题量身定制的训练算法,以及强化学习和不确定性建模。我们生活在一个激动人心的时代:这些方法具有巨大的潜力,可以从根本上改变计算机模拟所能实现的目标。
说明:v0.2有哪些新内容? 对于熟悉本书v0.1的读者来说,将DP集成到NN训练中的扩展章节和关于改进物理问题学习方法的全新章节(从标度-不变量和反演开始)是强烈推荐的起点。
即将推出
作为小预告,接下来的章节将有所展示:
- 如何训练网络来推断机翼等形状周围的流体流动,并估计预测的不确定性。这将提供一个替代模型,取代传统的数值模拟。
- 如何使用模型方程作为残差来训练代表解决方案的网络,以及如何通过使用可变模拟来改进这些残差约束。
- 如何针对逆问题与完整模拟器进行更紧密的交互。例如,我们将演示如何在训练循环中利用模拟器来规避标准强化学习技术的收敛问题。
- 我们还将讨论反演对于更新步骤的重要性,以及如何利用高阶信息来加快收敛速度,并获得更精确的神经网络。
在本文中,我们将介绍将物理模型引入深度学习的不同方法,即基于物理的深度学习(PBDL)方法。这些算法变体将按照整合紧密度递增的顺序进行介绍,并将讨论不同方法的利弊。重要的是,要知道每种不同的技术在哪些场景下特别有用。
可执行代码,就在此时此地
我们将重点介绍 Jupyter 笔记本,其主要优势在于所有代码示例都可以在浏览器中当场执行。您可以修改代码,并立即查看结果--请通过[在您的浏览器中运行这个预告示例]尝试一下。
此外,Jupyter 笔记本也很不错,因为它是一种有文化的编程。
意见和建议
本书由TUM的基于物理的仿真小组维护,其中 "书 "代表数字文本和代码示例集。如果您有任何意见,请随时通过老式电子邮件与我们联系。如果您发现错误,也请告知我们!我们知道这份文件远非完美,我们渴望改进它。在此先表示感谢!另外,我们还维护了一个链接集,其中包含最新的研究论文。
 ](http://physicsbaseddeeplearning.org/_images/divider-mult.jpg)
](http://physicsbaseddeeplearning.org/_images/divider-mult.jpg)
图 1 数值模拟时间序列的一些可视化示例。在本书中,我们将解释如何实现使用神经网络和数值求解器的算法。
谢谢!
如果没有许多人的帮助,这个项目就不可能完成。感谢大家 以下是按字母顺序排列的名单:
此外,还要感谢 Georg Kohl 提供漂亮的分隔线图像(参见 [KUT20] )、Li-Wei Chen 提供机翼数据图像,以及 Chloe Paillard 对本文部分内容的校对。
引用
如果您觉得本书有用,请通过以下方式引用:
@book{thuerey2021pbdl,
title={Physics-based Deep Learning},
author={Nils Thuerey and Philipp Holl and Maximilian Mueller and Patrick Schnell and Felix Trost and Kiwon Um},
url={https://physicsbaseddeeplearning.org},
year={2021},
publisher={WWW}
}
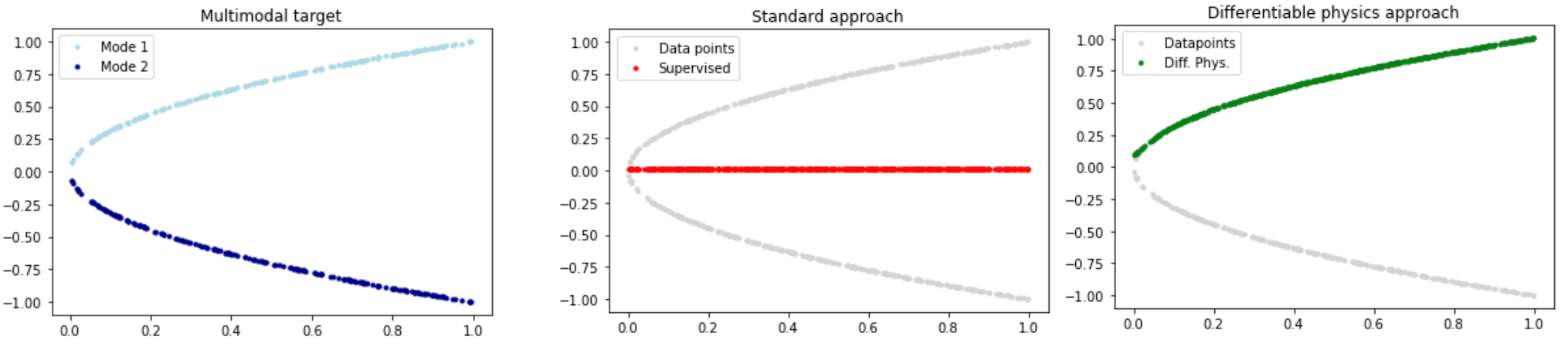
让我们从一个非常简化的例子开始,突出物理学习方法的一些关键能力。假设我们的物理模型是一个非常简单的方程:沿着正x轴的抛物线。
虽然非常简单,但每个x点都有两个解,即我们有两种模式,一个在x轴上方,另一个在下方,如下图左侧所示。如果我们不注意,传统的学习方法会给出一个完全错误的近似解,如下面中间图中红色线所示。通过改进学习设置,理想情况下通过使用离散化的数值求解器,我们至少可以准确表示解的一种模式(如右侧绿色线所示)。
1.1 可微物理学
下面章节的一个关键概念我们将其称之为可微物理学(Differentiable Physics,DP)。这意味着我们可以使用模型方程的领域知识,然后将这些模型的离散化版本整合到训练过程中。正如其名称所暗示的那样,具有可微的表达式对于支持神经网络的训练至关重要。
让我们通过以下示例来说明利用可微分物理进行深度学习的性质:我们希望找到一个未知函数,其接受来自的输入,并在空间中生成解,即。在接下来的内容中,我们经常用上标表示理想化的、未知的函数,其与没有这个上标的离散化、可实现的函数相对应。
另外假设我们有一个通用的微分方程(我们的“模型”方程),它编码了解的某种属性,例如我们希望匹配的某种真实世界的行为。接下来,通常代表时间演化,但它也可以是质量守恒的约束条件(那么将衡量散度)。但为了尽可能保持简单,在接下来的内容中,我们将关注一个将解映射回输入空间的模型,即。
通过使用神经网络来学习未知的理想函数,我们可以采用经典的“监督式”训练方法来通过收集数据获取。这种经典的设置需要通过从中采样,并添加相应的解来获得数据集。我们可以通过经典的数值技术来获取这些数据。然后,我们按照通常的方式利用这个数据集来训练神经网络。
与这种监督方法相比,采用可微分物理方法利用了一个事实:即我们通常可以使用物理模型 的离散化版本,并将其用于指导 的训练。也就是说,我们希望 知道我们的模拟器 ,并与其进行交互。这可以极大地改善学习效果,正如我们将在下面通过一个非常简单的例子进行说明的那样(更复杂的例子将在后面介绍)。
需要注意的是,为了使可微分物理方法起作用,正如其名称所暗示的那样,必须是可微分的。这些微分以梯度的形式出现,是推动学习过程的关键。
1.2 寻找抛物线的反函数
为了说明监督和可微分物理方法的区别,我们考虑以下简化的场景:给定函数 ,其中 在区间 内,需要找到未知函数 ,使得对于所有 内的 ,都满足 。注意:为了使事情更有趣,我们在这里使用 来表示 ,而不是更常见的抛物线 ,并且对于这个简单的情况,“离散化”只需要通过在计算机中用浮点数表示 和 来实现。
我们知道,的解可以是正或负的平方根函数(它们的分段组合也是可能的)。知道这并不是太困难,一个可行的解决方案是训练一个神经网络来近似这个逆映射。以经典有监督的方式(即纯粹基于数据)来实现这一点,显然是一个不错的起点,毕竟该方法已被证明是其他各种应用(如计算机视觉)的有力工具。
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
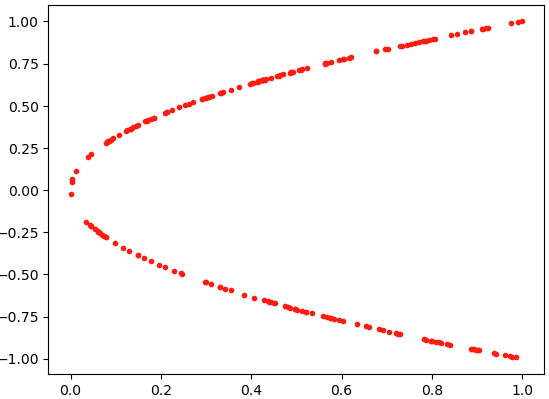
对于监督训练,我们可以使用求解器来预先计算训练所需的解:随机选择正或负平方根中的其中一个。这类似于一般情况,我们会收集所有可用的数据(例如使用优化技术来计算求解)。这种数据收集通常不会偏向于多模式解中的某个特定模式。
# X-Data
N = 200
X = np.random.random(N)
# Generation Y-Data
sign = (- np.ones((N,)))**np.random.randint(2,size=N)
Y = np.sqrt(X) * sign
利用代码显示图形:
plt.scatter(X,Y,s=9,color='red')
此时生成的点如图所示。
现在我们将使用一个简单的keras架构定义一个网络、损失函数和训练配置,该网络使用ReLU激活函数。
# Neural network
act = tf.keras.layers.ReLU()
nn_sv = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation=act, input_shape=(1,)),
tf.keras.layers.Dense(10, activation=act),
tf.keras.layers.Dense(1,activation='linear')])
我们可以通过一个简单的均方误差损失函数开始训练,使用Keras的fit函数进行训练:
# Loss function
loss_sv = tf.keras.losses.MeanSquaredError()
optimizer_sv = tf.keras.optimizers.Adam(learning_rate=0.001)
nn_sv.compile(optimizer=optimizer_sv, loss=loss_sv)
# Training
results_sv = nn_sv.fit(X, Y, epochs=5, batch_size= 5, verbose=1)
训练过程如下所示。
Epoch 1/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5084
Epoch 2/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5022
Epoch 3/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5011
Epoch 4/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5002
Epoch 5/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5007
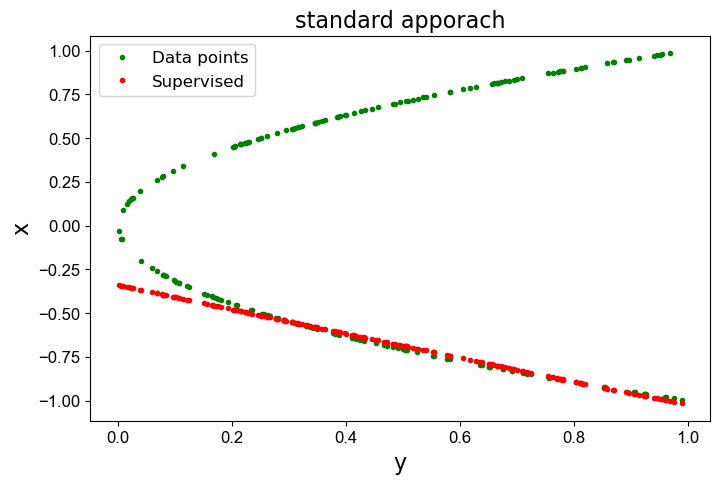
由于神经网络和数据集规模都非常小,训练计算非常迅速。然而如果我们检查网络的预测结果,我们会发现它与我们希望找到的解相去甚远:它在x轴两侧的数据点之间取平均值,因此无法找到满意的问题解。
下面的图表清楚地展示了这一点:它显示了原始数据(绿色)和监督解(红色)。
# Results
def draw(X,Y,Y_pre):
plt.figure(figsize=(8,5))
plt.plot(X,Y,'.',label = 'Data Point',color='green',zorder= 1)
plt.plot(X,Y_pre,'.',label='Supervised',color = 'red',zorder =2)
plt.xlabel('y',fontsize = 16)
plt.ylabel('x',fontsize = 16)
plt.title('standard apporach',fontsize = 16)
plt.yticks(fontproperties='Arial',size=12)
plt.xticks(fontproperties = 'Arial',size = 12)
plt.legend(fontsize = 12)
y_pre = nn_sv.predict(X)
draw(X,Y,y_pre)
结果如下图所示。

这显然是完全错误的!红线与绿色解相去甚远。
请注意,红线通常不是完全接近零,而在连续的情况下,解的两个模式应该取平均值。这是由于在这个例子中只有200个采样点,采样相对粗糙造成的。
1.3 可微物理方法
现在让我们应用可微分物理方法来找到:直接将离散模型纳入训练中。这里没有真实数据生成步骤;我们只需要从区间进行采样。
保持与先前情况相同的位置,并使用与之前架构相同的新的神经网络实例nn_dp:
# X-Data
# X = X , we can directly re-use the X from above, nothing has changed...
# Y is evaluated on the fly
# Model
nn_dp = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation=act, input_shape=(1,)),
tf.keras.layers.Dense(10, activation=act),
tf.keras.layers.Dense(1, activation='linear')])
损失函数是训练的关键点:我们直接将函数融入到损失函数中。 在这种简单的情况下,损失函数loss_dp只是简单地计算预测值y_pred的平方。
后来,这里可能会发生更多的事情:我们可以对预测解进行评估有限差分模板,或者计算求解器的整个隐式时间积分步长。 这里我们有一个简单的均方误差项,其形式为,我们在训练期间将其最小化。 没有必要让它变得如此简单:我们可以结合的知识和数值方法越多,我们就能更好地指导训练过程。
#Loss
mse = tf.keras.losses.MeanSquaredError()
def loss_dp(y_true, y_pred):
return mse(y_true,y_pred**2)
optimizer_dp = tf.keras.optimizers.Adam(learning_rate=0.001)
nn_dp.compile(optimizer= optimizer_dp,loss=loss_dp)
进行训练并显示结果:
#Training
results_dp = nn_dp.fit(X,X,epochs=5,batch_size = 5,verbose = 1)
y_pre = nn_dp.predict(X)
draw(X,Y,y_pre)
训练过程如下:
Epoch 1/5
40/40 [==============================] - 0s 656us/step - loss: 0.2814
Epoch 2/5
40/40 [==============================] - 0s 1ms/step - loss: 0.1259
Epoch 3/5
40/40 [==============================] - 0s 962us/step - loss: 0.0038
Epoch 4/5
40/40 [==============================] - 0s 949us/step - loss: 0.0014
Epoch 5/5
40/40 [==============================] - 0s 645us/step - loss: 0.0012
现在,网络实际上已经学会了抛物线函数的一个很好的反函数!下图用红色点显示计算解。
注意,红色的线可能是在上面,也可能是在下面,多次训练可能会得到不同的结果。比如出现下图的结果。
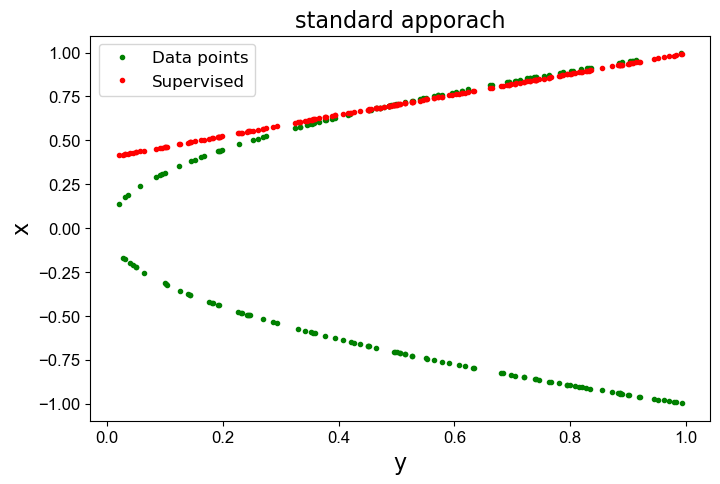
现在得到的结果要好多了。
这里发生了什么?
-
我们根据当前的网络预测值来评估离散模型,而不是使用预先计算好的解,从而避免了在求解中出现不希望出现的多种模式平均化现象。这样,我们就能在网络预测附近找到最佳模式,并防止求解流形中存在的模式平均化。
-
我们仍然只能得到曲线的一边!这是意料之中的,因为我们使用的是一个确定性函数来表示解。因此我们只能表示单一模式。有趣的是,是顶部模式还是底部模式由 中权重的随机初始化决定的,多运行几次示例就能看到这种效果。要捕捉多种模式,我们需要扩展 NN 以捕捉输出的完整分布,并用额外的维度对其进行参数化。
-
在本例中, 接近零的区域通常仍然是偏离的。在这里,网络基本上学习的是抛物线一半的线性近似值。造成这种情况的部分原因是神经网络的弱点:它非常小且浅。此外沿 x 轴均匀分布的样本点会使神经网络偏向于较大的 y 值。这些点对损失的贡献更大,因此网络会投入大部分资源来减少这一区域的误差。
1.4 讨论
这是一个非常简单的例子,但却非常清晰地展示了监督学习的失败案例。虽然乍一看似乎很不真实,但许多实际的 PDE 都会表现出各种各样的这些模式,而且我们通常并不清楚我们感兴趣的解空间中存在哪些模式以及它们的位置。在这种情况下使用监督学习是非常危险的,我们可能会在不知不觉中得到这些不同模式的平均值。
流体流动中的分岔就是一个明显的好例子。蜡烛上方升起的烟雾一开始是直的,然后由于其运动中的微小扰动,开始向随机方向摆动。下面的图片通过数值扰动说明了这种情况:完全对称的设置会开始向左或向右转动,这取决于近似误差如何积累。如果将这两种模式平均化,就会产生与上述抛物线示例类似的非物理直线流。
同样,我们在许多数值解中都有不同的模式,通常重要的是恢复它们,而不是将它们平均化。因此在接下来的章节中,我们将展示如何通过可微分物理来处理更实际、更复杂的情况。
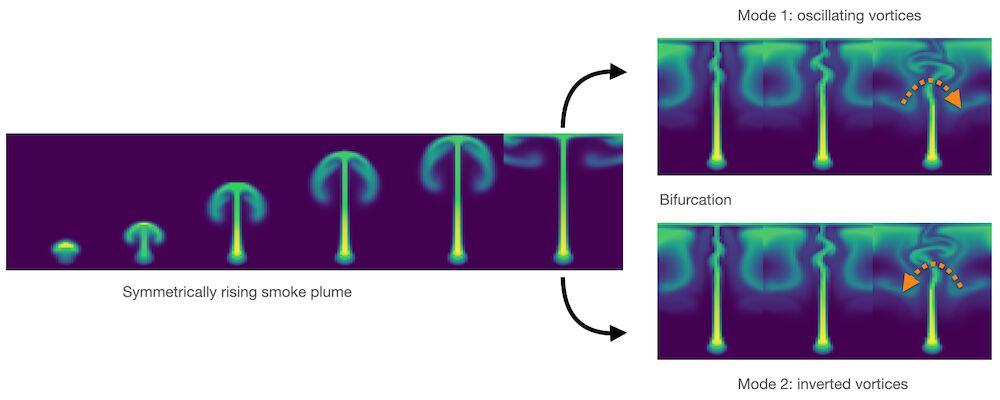
图2显示浮力驱动的流体流动中的分叉:绿色显示的“烟雾”开始以完全直线的方式上升,但随着时间的推移,微小的数值误差增长,导致涡旋向一侧(右上角)或相反方向(右下角)交替的不稳定性。
1.5 下一步
下面的每本笔记本都有一个 "下一步 "部分,比如下面这个部分,其中包含了关于从哪里开始修改代码的建议。毕竟,这些笔记本的全部意义就在于提供可随时执行的程序,作为自己实验的基础。为了减少笔记本的运行时间,示例的数据集和 NN 大小通常都很小,但它们仍然是潜在复杂大型项目的良好起点。
对于上述简单的 DP 例子:
-
本笔记本有意使用非常简单的设置。更改上述训练设置和 NN,可以获得更高质量的解,如顶部第一张图片中显示的绿色解。
-
或者尝试将设置扩展到二维情况,即抛物面。给定函数 ,找出一个反函数 ,使得 中的所有 都能得到 。
-
如果您想在不安装任何软件的情况下进行实验,也可以[在 colab 中运行此笔记本]。
本书名为 Physics-Based Deep Learning (基于物理的深度学习),意指将物理建模和数值模拟与基于人工神经网络的方法相结合。基于物理的深度学习的大方向代表了一个非常活跃、快速发展和令人兴奋的研究领域。接下来的章节将更详细地介绍这个主题,并为后续章节奠定基础。

图 4 了解我们的环境并预测其演化是人类面临的关键挑战之一。实现这些目标的一个重要工具是模拟,而下一代模拟将极大受益于整合深度学习组件,以便对我们的世界进行更准确的预测。
2.1 动机
从天气预报[Sto14](见上图),到量子物理学[OMalleyBK+16],再到等离子体聚变控制[MLA+19],利用数值分析来获得物理模型的解已成为科学研究不可分割的一部分。近年来,机器学习技术尤其是深度神经网络在多个领域取得了令人瞩目的成就:从图像分类[KSH12]到自然语言处理[RWC+19],以及最近的蛋白质折叠[Qur19]。该领域充满活力,发展迅速,前景广阔。
2.1.1 取代传统的模拟?
这些深度学习(DL)方法的成功案例引起了人们的关注,认为这种技术有可能取代传统的、模拟驱动的科学方法。例如,最近的研究表明,基于神经网络的代理模型达到了实际工业应用(如机翼流)所需的精度[CT21],同时在运行时间方面优于传统求解器几个数量级。
我们是否可以不依赖于仔细设计的基于基础原理的模型,而是通过处理足够大的数据集来提供正确的答案呢?正如我们将在接下来的章节中展示的那样,这种担忧是没有根据的。相反,对于下一代模拟系统来说,将传统的数值技术与深度学习方法相结合是至关重要的。
这种组合的重要性有一个核心原因,那就是深度学习方法强大的同时,也能从物理模型形式的领域知识中获益匪浅。深度学习技术和神经网络都比较新颖,有时应用起来比较困难,诚然,将我们对物理过程的理解妥善地融入到深度学习算法中往往并非易事。
在过去的几十年中,人们已经开发出高度专业和精确的离散方法来求解如 Navier-Stokes、Maxwell 或 Schroedinger 方程等基本模型方程。对离散方法进行的看似微不足道的改动却能决定在计算结果中是否能够看到关键的物理现象。本书非但不会抛弃数值数学领域已开发出的强大方法,反而会说明在应用深度学习时尽可能使用这些方法大有裨益。
2.1.2 黑匣子和魔法?
不熟悉 DL 方法的人通常会将神经网络与 黑盒子 联系在一起,并将训练过程视为人类无法理解的东西。然而这些观点通常源于道听途说和对这一主题了解不够。
相反,这种情况在科学界很常见:我们正在面对一类新的方法,而 所有的细节 还没有完全解决。这种情况在各种科学进步中都很常见。数值方法本身就是一个很好的例子。1950 年前后,数值逼近和求解器的地位十分艰难。例如,引用 H. Goldstine 的说法,数值不稳定性被认为是 未来焦虑的持续来源[Gol90]。现在,我们已经很好地掌握了这些不稳定性,数值方法无处不在,而且已经非常成熟。
因此,我们必须意识到,从某种程度上说,深度学习方法并不神奇或超凡脱俗。它们只是另一套数值工具。尽管如此,它们显然还是相当新的工具,而且现在绝对是我们所拥有的用于解决非线性问题的最强大的工具集。不能因为所有的细节还没有完全解决,还没有写得很好,就阻止我们将这些强大的方法纳入我们的数值工具箱。
2.1.3 协调DL和模拟
退一步说,本书的目的是利用我们所掌握的所有强大的数值模拟技术,并将它们与深度学习结合起来使用。因此,本书的核心目标是将以数据为中心的观点与物理模拟重新结合起来。
我们将讨论的关键问题包括:
- 解释如何使用深度学习技术来求解PDE问题
- 如何将它们与现有的物理学知识结合起来
- 不抛弃我们已有的关于数值方法的知识。
与此同时,值得注意的是,我们不会涵盖的内容包括:
- 深度学习和数值模拟的介绍,我们不打算对这一领域的研究文章进行广泛的研究
由此产生的方法在改进数值方法方面具有巨大潜力:例如,在求解器重复求解某个定义明确的问题领域中的案例时,投入大量资源训练一个支持重复求解的神经网络就非常有意义。基于该网络的特定领域专用性,这种混合网络的性能会大大超过传统的通用求解器。尽管还有很多问题有待解决,但第一批出版物已经证明,这一目标并不遥远[KSA+21, UBH+20]。
另一种看法是,我们自然界的所有数学模型都是理想化的近似值,都包含误差。为了获得非常好的模型方程,我们已经付出了很多努力,但为了向前迈进一大步,DL 方法提供了一个非常强大的工具,可以缩小与现实的差距[AAC+19]。
2.2 分类
在基于物理的深度学习领域,我们可以区分出从目标约束、组合方法、优化到应用的各种不同方法。更具体地说,所有方法要么针对正向模拟(预测状态或时间演化),要么针对反向问题(例如,从观测结果中获取物理系统的参数)。
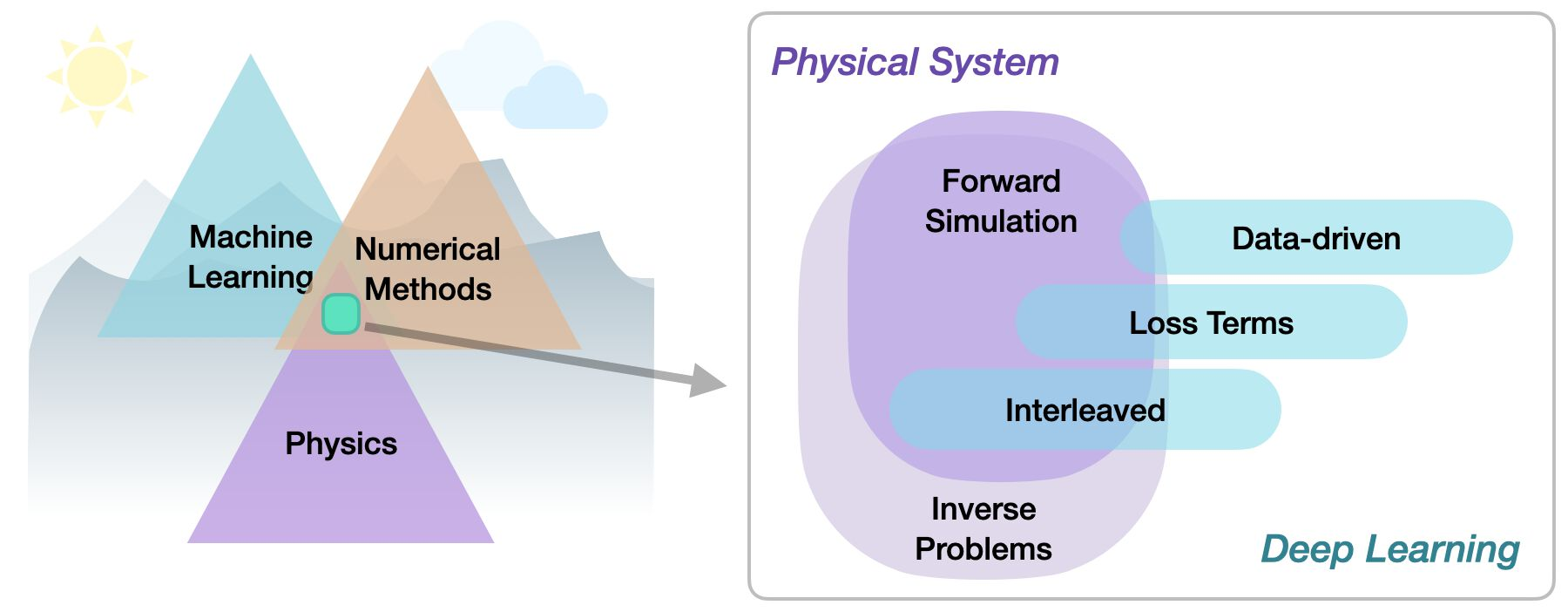
无论我们考虑的是正向问题还是反向问题,以下主题最关键的区别在于深度学习技术与领域知识(通常以偏微分方程(PDE)的形式)之间的整合方式的性质。基于物理学的深度学习(PBDL)技术大致可分为以下三类:
- 监督学习(Supervised:):数据由物理系统(真实或模拟)产生,但不存在进一步的交互。这是典型的机器学习方法。
- 损失项(Loss-terms):物理动力学(或其部分)通常以可微分算子的形式被编码在损失函数中。学习过程可以重复评估损失,并且通常从基于 PDE 的表达式中获得梯度。这些软约束有时也被称为“具有物理信息”的训练方法。
- 交织方法(Interleaved):完整的物理模拟与深度神经网络的输出交织并结合在一起。这需要一个完全可微分的模拟器,代表了物理系统与学习过程之间最紧密的耦合。交织式可微分物理方法在时间演化中尤为重要,其可以为动力学的未来行为做出估计。
因此,可以根据正向求解与反向求解以及物理模型在训练深度神经网络的优化循环中的紧密程度进行分类。在这里,特别是利用“可微分物理”进行交织的方法允许深度学习和数值模拟方法之间的非常紧密的集成。
2.2.1 命名
值得指出的是,在接下来的内容中,我们所称谓的可微分物理学 (Differentiable Physics,DP)在其他资源和研究论文中有多种不同的名称。可微分物理学的名称受到深度学习中可微分编程范式的启发。在这里,例如我们还有可微分渲染方法,用于模拟光线如何形成我们作为人类所看到的图像。相比之下,我们将从现在开始专注于物理模拟,因此才有了这个名字。
然而,来自其他背景的人更常用其他名称。例如可微分物理方法等效于使用伴随方法(adjoint method),并将其与深度学习过程相结合。实际上,它也等效于将反向传播/反向模式微分应用于数值模拟。然而正如上面所提到的,出于对深度学习观点的考虑,从现在开始我们将统称这些方法为可微分物理方法。
2.3 展望未来
物理模拟是一个庞大的领域,我们无法涵盖所有可能的物理模型和模拟类型。
注意本书的重点在于:
- 基于场的模拟(没有拉格朗日方法)
- 与深度学习的结合(存在其他许多有趣的机器学习技术,但这里不讨论)
- 实验留作展望(即用真实世界的观测数据取代合成数据)
值得注意的是,我们正从一些非常基本的构建模块开始构建这些方法。以下是跳过后面章节的一些注意事项。
提示:如果满足以下条件,可以跳过...
- 非常熟悉数值方法和偏微分方程求解器,并且希望立即开始DL主题。那么监督训练章节是一个很好的起点。
- 另一方面,如果已经深入NNs&Co,并且想跳过研究相关主题,我们建议从物理损失项章节开始,这为下一章奠定了基础。
不过,在这两种情况下,简单了解一下我们在符号和缩写 章节中的 符号 并不会有什么坏处!
2.4 实现
这段文字还介绍了一系列深度学习和模拟API的概述。我们将使用流行的深度学习API,[如pytorch](https://pytorch.org]和 tensorflow,并且额外介绍了可微分模拟框架 ΦFlow (phiflow) 。其中一些示例也使用了JAX。因此,通过学习这些示例,您应该对当前API中提供的功能有一个很好的概览,从而可以为新任务选择最适合的API。
由于我们(在大多数Jupyter笔记本示例中)处理的是随机优化问题,因此下面的许多代码示例每次运行时都会产生稍微不同的结果。这在神经网络训练中非常常见,但在执行代码时要牢记这一点。这也意味着文本中讨论的数字可能与您重新运行示例后看到的数字并不完全一致。
2.5 模型与方程
下面我们将简要介绍深度学习(真的是非常非常简要!),主要是为了介绍符号表示法。
此外,我们将在下面讨论一些模型方程。请注意,与其他一些文本和API不同,我们将避免使用Model来表示经过训练的神经网络。它们将被称为NNs(神经网络)或networks(网络)。这里的Model(模型)通常表示一组描述物理效应的模型方程,它们通常是偏微分方程(PDEs)。
2.5.1 深度学习与神经网络
在本书中,我们专注于与物理模型的联系,而深度学习有很多很棒的介绍。因此,我们将保持简短:深度学习的目标是近似一个未知函数: 其中, 表示参考解或真实解。应该用NN表示来近似。我们通常借助损失函数 的某种变体来确定 ,其中 是 NN 的输出。这就给出了一个最小化问题,即找到 使得 最小化。在最简单的情况下,我们可以使用 误差,得出 通常,我们使用随机梯度下降(SGD)优化器(例如Adam [KB14])对其进行优化,即训练。我们将依赖于自动微分来计算损失函数相对于权重的梯度。对于梯度计算来说,这个函数是标量且非常重要,损失函数通常也被称为误差函数、成本函数或目标函数。
对于训练,我们要区分:从某种分布中提取的训练数据集、验证数据集(来自相同的分布,但数据不同),以及与训练数据集有某种不同分布的测试数据集。后一种区别非常重要。对于测试集,我们需要 超出分布范围(OOD)的数据,以检查训练模型的泛化效果。需要注意的是,这就为测试数据集提供了一个巨大的可能性范围:从肯定会起作用的微小变化,到基本上保证会失败的完全不同的输入。虽然没有黄金标准,但在生成测试数据时仍需谨慎。
如果以上内容对你来说还不够明显,我们强烈建议阅读《深度学习》这本书的第6章至第9章,尤其是关于多层感知器(MLPs)和卷积神经网络(CNNs)的部分。你可以在深度学习的链接中找到这些章节,分别是MLPs和Conv-Nets,即卷积神经网络(CNNs)。
分类问题和回归问题之间的经典 ML 区别在这里并不重要:下面的内容中,我们只讨论回归问题。
2.5.2 作为物理模型的偏微分方程
接下来的部分将简要介绍稍后在深度学习示例中所使用到的一些模型方程。我们的目标通常是连续的偏微分方程,用 表示,其解处在 维的空间域 中。此外我们还经常考虑方程在有限时间间隔 内的演化过程。相应的物理场可以是 d 维向量场,例如 ,也可以是标量场 。向量的分量通常用下标表示,即(当时),而位置则用表示。
为了得到 的唯一解,我们需要指定合适的初始条件,通常是在 时的所有相关物理量,以及 边界的边界条件,在下文中用 表示。
表示一个连续的公式,我们对其连续性做了轻微的假设,通常我们会假设其存在一阶导数和二阶导数。
然后,我们可以使用数值方法,通过离散化获得平滑函数的近似值,如 。这必然会引入离散化误差,我们希望误差越小越好。这些误差可以用与精确分析解的偏差来衡量,对于离散模拟 PDEs,它们通常表示为截断误差 的函数,其中 表示离散化的空间步长。同样,我们通常通过时间步长 进行时间离散化。
我们通过执行大小为 的步长来求解一个离散的偏微分方程。解可以表示为 及其导数的函数:,其中 表示空间导数 。
接下来,我们将对模型方程进行概述,然后在后续章节及性能实际模拟和实现示例。
2.5.3 一些PDE示例
以下PDEs是很好的例子,我们将在不同的设置中使用它们来展示如何将它们纳入到深度学习中。
Burgers方程
我们经常以一维或二维的Burgers方程作为起点。这是一个经过广泛研究的偏微分方程,与Navier-Stokes方程不同,该方程不包含任何额外的约束条件(如质量守恒)。因此,它会导致有趣的激波形成。Burgers方程包含一个对流项(运动/输运)和一个扩散项(由热力学第二定律引起的耗散)。
二维Burgers方程表示为: 式中,及分别表示扩散常数和外力。
在没有外力的情况下,,将单个一维速度分量表示为,可以得到burgers方程在一维空间中简单的变体: Navier-Stokes方程
就复杂性而言,Navier-Stokes方程是一个很好的下一步,它是一个成熟的流体模型。除了动量守恒方程(类似于Burgers方程)外,该方程还包括质量守恒方程。这可以防止激波的形成,但同时为数值方法引入了新的挑战,即添加了无散度运动的硬约束条件。
在二维情况下,没有任何外部力的Navier-Stokes方程可以写成: 其中,像前面一样,𝜈 为粘度。
NS方程一个有趣的变体是通过包含Boussinesq近似来考虑温度对流体密度的影响。使用一个标记场来指示高温区域,可以得到以下方程组: 其中𝜉表示浮力的强度。
最后,3D中的Navier-Stokes模型给出了以下方程组:
2.5.4 正向模拟
在我们真正开始学习方法之前,有必要介绍一下使用上述模型方程的最基本的变体:常规的 正向 模拟,即从一组初始条件开始,随着时间的推移,用模型方程的离散版本演化系统的状态。我们将展示如何对一维burgers方程和二维的Navier-Stokes模拟进行这种正向模拟。
2.6 用phiflow对Burgers方程进行正演模拟
本章将介绍如何运行“正向”即常规模拟,即从给定的初始状态开始,通过数值逼近来近似后续状态,并介绍ΦFlow框架。ΦFlow提供了一组可微分的构建模块,可以直接与深度学习框架进行接口,因此非常适合本书的主题。在深入和更复杂的集成之前,本章(以及下一章)将展示如何使用ΦFlow进行常规模拟。随后,我们将展示如何轻松将这些模拟与神经网络进行耦合。
ΦFlow的主要代码库(以下简称为"phiflow")位于https://github.com/tum-pbs/PhiFlow,您可以在https://tum-pbs.github.io/PhiFlow/找到其他API文档和示例。
对于这个jupyter笔记本(以及后续的笔记本),你可以在第一个段落的末尾找到一个“[在Colab中运行]”的链接(或者你可以使用页面顶部的启动按钮)。这将在Colab中加载PBDL GitHub仓库中的最新版本的笔记本,你可以立即执行它:在Colab中运行。
2.6.1 Model
我们使用Burgers方程作为物理模型。这个方程是一个非常简单、非线性且非平凡的模型方程,可以导致有趣的冲击波形成。因此它是我们进行实验的一个很好的起点,该方程的一维版本(方程(4))如下所示:
2.6.2 导入和加载Phiflow
让我们先做一些准备工作:首先,我们将导入phiflow库,更具体地说是用于流体模拟的numpy运算符:phi.flow(用于DL框架X的可微分版本则通过phi.X.flow加载)。
注意: 下面的第一条带有"!"前缀的命令将通过pip在您的Python环境中安装来自GitHub的phiflow Python包。我们假设您尚未安装phiflow,但如果您已经安装了,请注释掉第一行(对于后续的所有笔记本也是如此)。
!pip install --upgrade --quiet phiflow==2.2
from phi.flow import *
注意:这里如果提示dtype错误,则需要修改C:\ProgramData\anaconda3\Lib\site-packages\phi\math\backend_dtype.py文件,修改第135行为
DType(object): np.dtype('O'),,修改第139行为_FROM_NUMPY[np.bool_] = DType(bool)。主要原因是numpy升级后抛弃了np.object及np.bool。如果是低版本的numpy则不会报错。
接下来,可以定义并初始化必要的常量(用大写字母表示):模拟域具有N=128个单元格作为1D速度的离散点,这些离散点位于在周期性域上的区间内。我们将使用32个时间步长STEPS,时间间隔为1,因此我们得到DT=1/32。此外,我们将使用粘度NU为。
我们还将定义一个初始状态,由numpy数组INITIAL_NUMPY中的给出,我们将在下一个单元格中使用它来初始化模拟中的速度。此初始化将在计算域的中心产生一个漂亮的冲击波。
Phiflow是面向对象的,以场数据形式(由张量对象在内部表示)为中心。也就是说,您通过构建一些网格来组装模拟,并在时间步长内更新它们。
Phiflow在内部使用带有命名维度的张量。这在后面处理具有附加批处理和通道维度的2D模拟时将非常方便,但现在我们只需将1D数组简单地转换为具有单个空间维度'x'的phiflow张量即可。
N = 128
DX = 2./N
STEPS = 32
DT = 1./STEPS
NU = 0.01/(N*np.pi)
# initialization of velocities, cell centers of a CenteredGrid have DX/2 offsets for linspace()
INITIAL_NUMPY = np.asarray( [-np.sin(np.pi * x) for x in np.linspace(-1+DX/2,1-DX/2,N)] ) # 1D numpy array
INITIAL = math.tensor(INITIAL_NUMPY, spatial('x') ) # convert to phiflow tensor
接下来,我们从转换为张量的INITIAL numpy数组中初始化一个1D velocity 网格。
我们通过bounds参数来指定域的范围,并且网格使用周期性边界条件(extrapolation.PERIODIC)。这两个属性是张量和网格之间的主要区别:后者具有边界条件和物理范围。
为了便于说明,我们还将输出有关速度对象的一些信息:它是一个大小为128的phi.math张量。请注意,实际的网格内容包含在网格的values中。下面我们使用numpy()函数将phiflow张量的内容转换为numpy数组,并输出其中的五个条目。对于具有更多维度的张量,我们需要在这里指定额外的维度,例如,对于一个2D速度场,我们会使用'y,x,vector'(对于只有单个维度的张量,我们可以省略它)。
velocity = CenteredGrid(INITIAL, extrapolation.PERIODIC, x=N, bounds=Box('x',-1:1))
vt = advect.semi_lagrangian(velocity, velocity, DT)
print(`Velocity tensor shape: ` + format( velocity.shape )) # == velocity.values.shape
print(`Velocity tensor type: ` + format( type(velocity.values) ))
print(`Velocity tensor entries 10 to 14: ` + format( velocity.values.numpy('x')[10:15] ))
输出结果为:
Velocity tensor shape: (x=128)
Velocity tensor type: <class 'phi.math._tensors.CollapsedTensor'>
Velocity tensor entries 10 to 14: [0.49289819 0.53499762 0.57580819 0.61523159 0.65317284]
2.6.3 运行模拟
现在我们可以准备运行模拟了。为了计算模型方程中的扩散和对流分量,我们可以简单地调用phiflow中现有的diffusion和semi_lagrangian运算符:diffuse.explicit(u,...)通过中心差分计算模型中项的显式扩散。接下来,advect.semi_lagrangian(f,u)用于通过速度u对任意场f进行稳定的一阶逼近输运。在模型中有,因此可以使用semi_lagrangian函数在实现中将速度与自身进行输运:
velocities = [velocity]
age = 0.
for i in range(STEPS):
v1 = diffuse.explicit(velocities[-1], NU, DT)
v2 = advect.semi_lagrangian(v1, v1, DT)
age += DT
velocities.append(v2)
print(`New velocity content at t={}: {}`.format( age, velocities[-1].values.numpy('x,vector')[0:5] ))
输出结果为:
New velocity content at t=1.0: [[0.0057228 ]
[0.01716715]
[0.02861034]
[0.040052 ]
[0.05149214]]
在这里,我们实际上将所有时间步收集到列表velocities中。一般来说,这并不是必需的(并且对于长时间运行的模拟可能会消耗大量内存),但在这里可以用于后续速度状态演变的绘制。
print语句输出了一些速度值,已经表明我们的模拟正在发生一些事情,但很难从这些数字中直观地了解 PDE 的行为。因此,让我们将随时间变化的状态可视化,以显示正在发生的事情。
2.6.4 可视化
我们可以很容易地通过图表直观地看到这种一维情况:下面的代码用蓝色显示初始状态,然后用绿色、青色和紫色显示 的时间。
# get `velocity.values` from each phiflow state with a channel dimensions, i.e. `vector`
vels = [v.values.numpy('x,vector') for v in velocities] # gives a list of 2D arrays
import pylab
fig = pylab.figure().gca()
fig.plot(np.linspace(-1,1,len(vels[ 0].flatten())), vels[ 0].flatten(), lw=2, color='blue', label=`t=0`)
fig.plot(np.linspace(-1,1,len(vels[10].flatten())), vels[10].flatten(), lw=2, color='green', label=`t=0.3125`)
fig.plot(np.linspace(-1,1,len(vels[20].flatten())), vels[20].flatten(), lw=2, color='cyan', label=`t=0.625`)
fig.plot(np.linspace(-1,1,len(vels[32].flatten())), vels[32].flatten(), lw=2, color='purple',label=`t=1`)
pylab.xlabel('x'); pylab.ylabel('u'); pylab.legend()
输出结果如图所示。

这很好地显示了在我们的区域中心形成的激波,它是由两个初始速度 凸起(左侧的正凸起(向右移动)和中心右侧的负凸起(向左移动))碰撞形成的。
由于这些线条可能会有很多重叠,我们在接下来的章节中还将使用另一种可视化方法,即在二维图像中显示所有时间步长的演变过程。我们的一维域将沿 Y 轴显示,沿 X 轴的每个点代表一个时间步长。
下面的代码将我们的速度状态集合转换为二维数组,将单个时间步长重复 8 次,以使图像更宽。当然,这完全是可有可无的,但却能让我们更容易地看到汉堡模拟中发生的事情。
import os
def show_state(a, title):
# we only have 33 time steps, blow up by a factor of 2^4 to make it easier to see
# (could also be done with more evaluations of network)
a = np.expand_dims(a, axis=2)
for i in range(4):
a = np.concatenate([a, a], axis=2)
a = np.reshape(a, [a.shape[0], a.shape[1]*a.shape[2]])
#print(`Resulting image size` +format(a.shape))
fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
im = axes.imshow(a, origin='upper', cmap='inferno')
pylab.colorbar(im)
pylab.xlabel('time')
pylab.ylabel('x')
pylab.title(title)
vels_img = np.asarray(np.concatenate(vels, axis=-1), dtype=np.float32)
# save for comparison with reconstructions later on
os.makedirs(`./temp`, exist_ok=True)
np.savez_compressed(`./temp/burgers-groundtruth-solution.npz`,np.reshape(vels_img, [N, STEPS+1]))
show_state(vels_img, `Velocity`)
运行结果为:

至此,phiflow 的首次模拟结束。它并不太复杂,但正因为如此,它为下一章评估和比较不同的基于物理的深度学习方法提供了一个良好的起点。不过在此之前,我们将在下一节针对更复杂的模拟类型进行研究。
2.6.5 后续步骤
在此模拟设置的基础上进行一些尝试:
- 请随意尝试 - 上述设置非常简单,您可以更改模拟参数或初始化。例如,可以通过
Noise()使用噪声场来获得更混乱的结果(参见上文速度单元中的注释)。 - 更复杂一点:将模拟扩展到 2D(或更高)。这需要对整个程序进行修改,但上述所有运算符都支持更高维度。在尝试之前,您可能需要查看下一个示例,它涵盖了一个 2D Navier-Stokes 案例。
2.7 Navier-Stokes 正向模拟
现在让我们举一个更复杂的例子:基于纳维-斯托克斯方程的流体模拟。使用 ΦFlow (phiflow)仍然非常简单,因为这里存在所有步骤的可微分算子。纳维-斯托克斯方程(不可压缩形式)引入了额外的压力场 ,以及质量守恒约束。我们还将随着气流移动一个标记场,这里用 表示。它表示温度较高的区域,并通过浮力因子产生作用力:
在这里,我们的目标是无压缩流 (即 ), 并通过项 使用一个简单的浮力模型 (Boussinesq 近似)。这在不显式计算 的情况下为无压缩求解器近似了密度的变化。我们假设一个沿 y 方向作用的重力力, 通过向量 。
我们将在一个封闭域上求解这个 PDE,该域的速度边界条件为 ,压力边界条件为 ,该域的物理尺寸为 单位。[run in colab]
2.7.1 实现
与上一节一样,第一条带!前缀的命令是在 python 环境中通过pip安装来自 GitHub 的 phiflow python 软件包。(如有必要,可跳过或修改此命令)。
from phi.flow import * # The Dash GUI is not supported on Google colab, ignore the warning
import pylab
2.7.2 设置模拟
下面的代码会设置一些常数,这些常数用大写字母表示。我们将使用 单元来离散域,通过 引入轻微的粘性,并定义时间步长为 。
我们首先创建一个 CenteredGrid,它由一个 Sphere 几何对象初始化。这将表示热烟雾生成的入流区域 INFLOW。
DT = 1.5
NU = 0.01
INFLOW = CenteredGrid(Sphere(center=tensor([30,15], channel(vector='x,y')), radius=10), extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,80),y=(0,100))) * 0.2
流入的烟雾将被注入第二个居中的网格 smoke 中,该网格代表上面的标记字段 。请注意,我们在上面定义了一个大小为 的 Box。这是在我们的模拟中以空间单位表示的物理尺度,也就是说, 的速度将使烟雾密度每 1 个时间单位移动 1 个单位,这可能大于或小于离散网格中的一个单元,具体取决于 x,y 的设置。您可以将模拟网格参数设置为直接类似于现实世界的单位,或者考虑适当的换算因子。
上面的入流球体已经使用“世界”坐标: 它位于第一个轴上的 , (在 的域框内)。
接下来,我们为要模拟的量创建网格。在本例中,我们需要速度场和烟雾密度场。
smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,80),y=(0,100))) # sampled at cell centers
velocity = StaggeredGrid(0, extrapolation.ZERO, x=32, y=40, bounds=Box(x=(0,80),y=(0,100))) # sampled in staggered form at face centers
我们以交错形式对单元中心的烟场和速度进行采样。交错网格内部包含 2 个不同维度的居中网格,可通过 unstack 函数转换为居中网格(或简单的 numpy 数组),如上文链接中所述。
接下来,我们定义模拟的更新步骤,调用必要的函数将流体系统的状态向前推进 dt。下一个单元将计算一个这样的步骤,并绘制一个模拟帧后的标记密度图。
def step(velocity, smoke, pressure, dt=1.0, buoyancy_factor=1.0):
smoke = advect.semi_lagrangian(smoke, velocity, dt) + INFLOW
buoyancy_force = (smoke * (0, buoyancy_factor)).at(velocity) # resamples smoke to velocity sample points
velocity = advect.semi_lagrangian(velocity, velocity, dt) + dt * buoyancy_force
velocity = diffuse.explicit(velocity, NU, dt)
velocity, pressure = fluid.make_incompressible(velocity)
return velocity, smoke, pressure
velocity, smoke, pressure = step(velocity, smoke, None, dt=DT)
print(`Max. velocity and mean marker density: ` + format( [ math.max(velocity.values) , math.mean(smoke.values) ] ))
pylab.imshow(np.asarray(smoke.values.numpy('y,x')), origin='lower', cmap='magma')
在这个 step() 调用中发生了很多事情:我们平移了烟场,通过Boussinesq 模型添加了一个向上的力,平移了速度场,最后通过压力求解使其无发散。
布尔辛斯克模型使用(0, buoyancy_factor) 元组乘法将烟场转化为交错的 2 分力场,并通过 at() 函数在速度分量的位置进行采样。该函数可确保交错速度分量的各个力分量被正确插值。请注意,这也会直接确保保留原始网格的边界条件。它还会在内部对生成的力网格执行 StaggeredGrid(..., extrapolation.ZERO,...) 内插。
在 make_incompressible 中的压力投影步骤通常是上述序列中计算成本最高的步骤。它根据域的边界条件求解泊松方程,并根据计算出的压力梯度更新速度场。
为了测试,我们还打印了更新后的速度平均值和最大密度。从生成的图像中可以看到,第一轮烟雾区域有轻微的向上运动(此处尚未显示)。
2.7.3 数据类型和尺寸
我们在这里为模拟字段创建的变量是Grid 类的实例。与张量一样,网格也有 shape 属性,该属性列出了所有批次、空间和通道维度。phiflow中的形状不仅存储了维度的大小,还存储了它们的名称和类型。
print(f"Smoke: {smoke.shape}")
print(f"Velocity: {velocity.shape}")
print(f"Inflow: {INFLOW.shape}, spatial only: {INFLOW.shape.spatial}")
请注意,这里的 phiflow 输出显示了维度的类型,例如, 表示空间维度, 表示向量维度。在后面的学习中,我们还将引入批量维度。
我们可以通过 .sizes获取形状对象的实际内容,或者通过 .get_size('dim')查询特定维度 dim 的大小。下面是两个示例:
print(f"Shape content: {velocity.shape.sizes}")
print(f"Vector dimension: {velocity.shape.get_size('vector')}")
可以使用 values 属性访问网格值。这是与 phiflow 张量对象的一个重要区别,后者没有values,如下代码示例所示。
print("Statistics of the different simulation grids:")
print(smoke.values)
print(velocity.values)
# in contrast to a simple tensor:
test_tensor = math.tensor(numpy.zeros([3, 5, 2]), spatial('x,y'), channel(vector="x,y"))
print("Reordered test tensor shape: " + format(test_tensor.numpy('vector,y,x').shape) ) # reorder to vector,y,x
#print(test_tensor.values.numpy('y,x')) # error! tensors don't return their content via ".values"
网格还有更多的特性,这里 有详细记录。还要注意的是,交错网格具有非均匀形状,因为网格面的数量与单元格的数量不相等(在本例中,x 部分的单元格数量是 40 的 31 次方,而 y 部分的单元格数量是 39 的 32 次方)。INFLOW "网格的尺寸自然与 "smoke "网格相同。
2.7.4 时间演化
有了这种设置,我们就可以通过反复调用 step 函数,轻松地将模拟时间向前推进一些。
for time_step in range(10):
velocity, smoke, pressure = step(velocity, smoke, pressure, dt=DT)
print('Computed frame {}, max velocity {}'.format(time_step , np.asarray(math.max(velocity.values)) ))
现在,热羽流开始上升:
pylab.imshow(smoke.values.numpy('y,x'), origin='lower', cmap='magma')

让我们再计算并展示几个模拟步骤。由于流入的水流偏离中心向左(X 位置为 30),因此当羽流撞击到域的顶壁时会向右弯曲。
steps = [[ smoke.values, velocity.values.vector[0], velocity.values.vector[1] ]]
for time_step in range(20):
if time_step<3 or time_step%10==0:
print('Computing time step %d' % time_step)
velocity, smoke, pressure = step(velocity, smoke, pressure, dt=DT)
if time_step%5==0:
steps.append( [smoke.values, velocity.values.vector[0], velocity.values.vector[1]] )
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
axes[i].imshow(steps[i][0].numpy('y,x'), origin='lower', cmap='magma')
axes[i].set_title(f"d at t={i*5}")
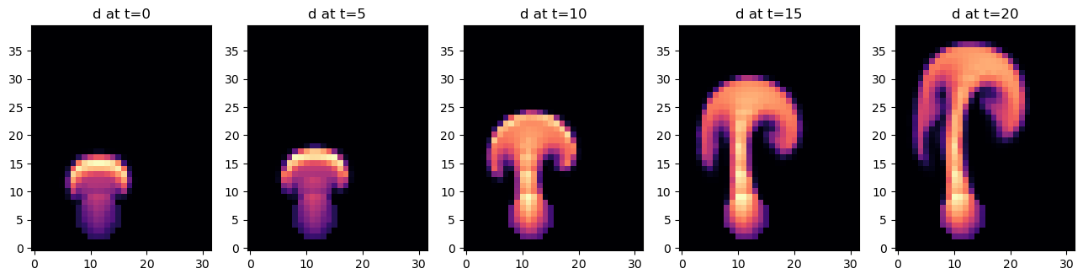
我们还可以看看速度。上面的 steps 列表已经将速度的 vector[0] 和 vector[1] 分量存储为 numpy 数组,接下来我们可以展示一下。
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
axes[i].imshow(steps[i][1].numpy('y,x'), origin='lower', cmap='magma')
axes[i].set_title(f"u_x at t={i*5}")
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
axes[i].imshow(steps[i][2].numpy('y,x'), origin='lower', cmap='magma')
axes[i].set_title(f"u_y at t={i*5}")
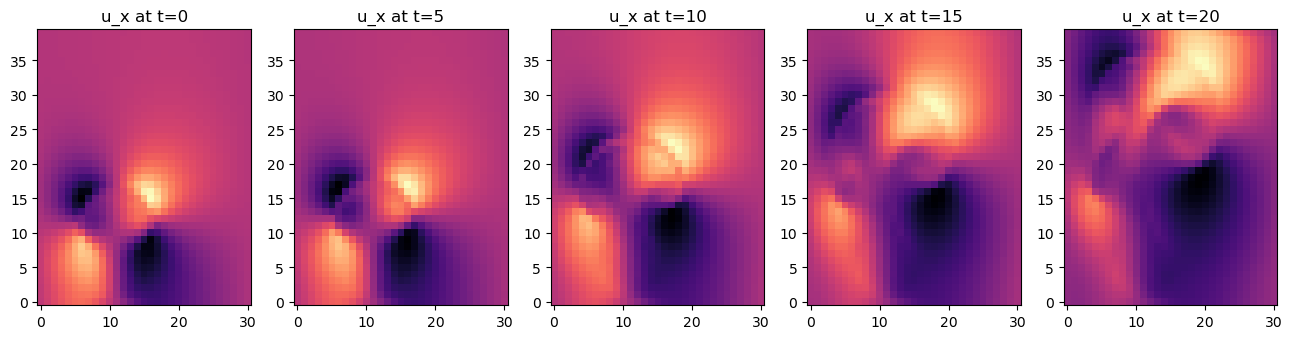

这里看起来很简单,但这个模拟设置却是一个功能强大的工具。仿真可以很容易地扩展到更复杂的情况或三维空间,而且它已经与深度学习框架的反向传播管道完全兼容。
在接下来的章节中,我们将展示如何使用这些模拟来训练 NN,以及如何通过训练好的 NN 来引导和修改它们。这将说明通过在循环中加入求解器,我们可以在多大程度上改进训练过程,尤其是当求解器是可变的时候。在进入这些更复杂的训练过程之前,我们将在下一章介绍一种更简单的监督方法。这一点非常重要:即使是针对基于物理的高级学习设置,有效的监督训练始终是第一步。
2.7.5 下一步
您可以在此基础上创建各种流体模拟。例如,尝试改变空间分辨率、浮力系数和模拟运行的总长度。
2.8 优化和收敛性
本章将概述不同优化算法的推导过程。与其他文章不同的是,我们将从牛顿法这一经典优化算法入手,推导出几种广泛使用的变体,然后再回到深度学习(DL)优化器。我们的主要目标是将 DL 纳入这些经典方法的范畴。虽然我们将专注于 DL,但我们也会在本书稍后部分重温经典算法,以改进学习算法。物理模拟夸大了神经网络造成的困难,这就是为什么下面的主题与基于物理的学习任务特别相关。
2.8.1 符号
本章使用一种自定义符号,这种符号经过精心挑选,可以清晰简要地表示所考虑的所有方法。我们有一个标量损失函数 ,最佳值( 的最小值)位于位置 , 表示在 中的一个步。中不同的中间更新步用下标表示,如或。
本章使用经过仔细选择的自定义符号, 以清晰简洁地表示正在考虑的所有方法。我们有一个标量损失函数 ,最优点 (L 的最小值)在 处, 表示 中的一步。 中的不同中间更新步骤用下标表示, 例如 或 。
在下文中,我们经常需要取反,即除以某个量。对于矩阵 和 ,我们定义 。当 和 是向量时,结果就是用下面两种公式之一得到的矩阵。我们将具体说明使用哪一种:
将 应用于 一次,可以得到雅各布值 。由于 是标量, 是行向量,梯度(列向量) 由 给出。再次应用 可以得到 Hessian 矩阵 ,再次应用 可以得到第三导数张量,用 表示。幸运的是,我们从来不需要把 作为一个完整的张量来计算,但在下面的一些推导中需要用到它。为了缩短下面的符号,当函数或导数在 处求值时,我们通常会去掉 ,例如, 将表示为 。
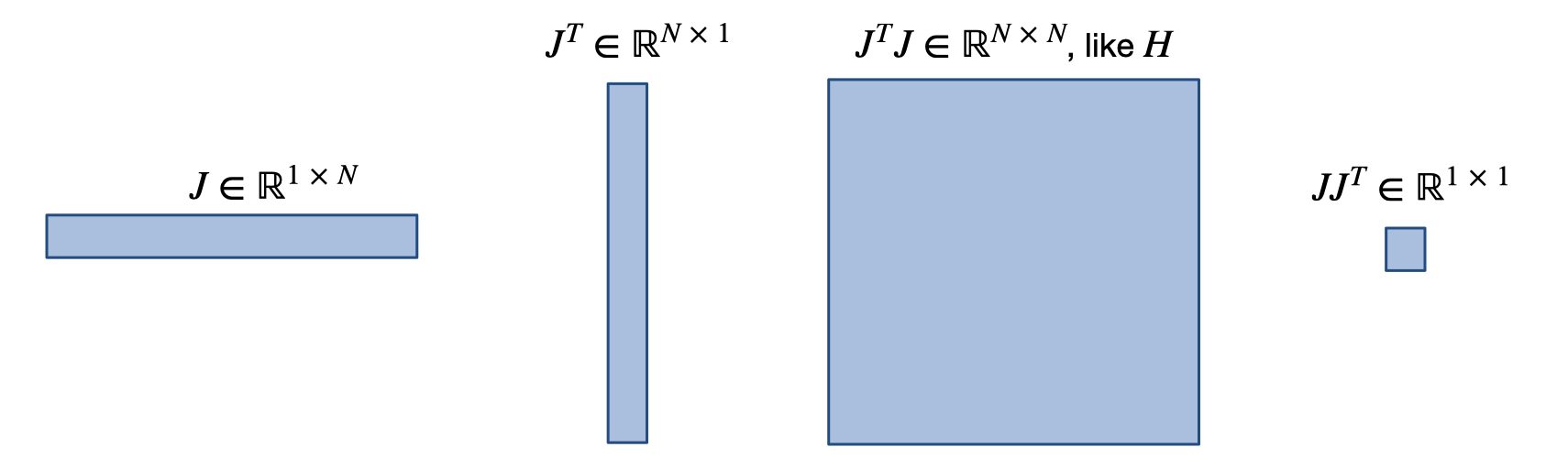
下图概述了一些常用量的矩阵形状。之后我们就不需要它了,但在本图中,表示的维度,即。
2.8.2 准备工作
我们需要一些工具来进行下面的推导,现将其总结如下,以供参考。
毫不奇怪,我们需要一些泰勒级数展开式。用上面的符号表示为
然后,我们还需要拉格朗日形式,它可以从区间 中得到 的精确解:
在一些情况下,我们会用到微积分基本定理,为了完整起见,在此重复一遍:
此外,我们还将利用具有常数 的 Lipschitz连续性: ,以及著名的 Cauchy-Schwartz 不等式:。
2.8.3 牛顿法
现在,我们可以从最经典的优化算法开始:牛顿法它是通过将我们感兴趣的函数近似为抛物线而得出的。这是因为几乎所有的最小值近看都像抛物线。
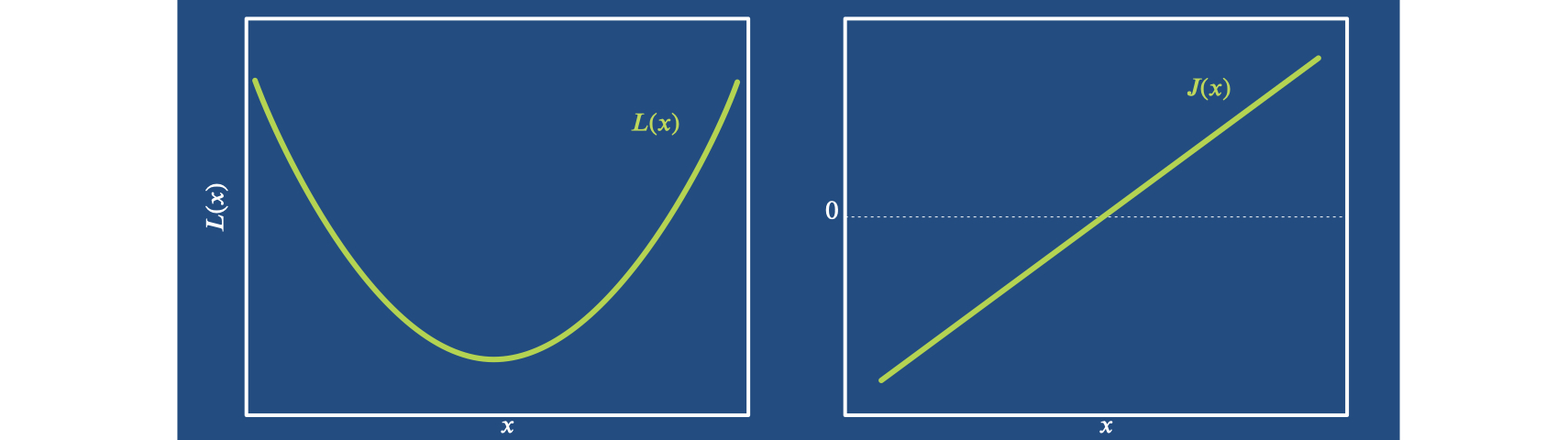
因此,我们可以用抛物线的形式 来表示最佳值 附近的 。其中表示常数偏移。在位置 处,我们观察到 和 。将其重新排列后,可以直接得出计算最小值的方程:。牛顿法默认以单步计算 ,因此牛顿法中的 更新量给定为:
让我们来看看牛顿法的收敛阶次。对于 的最优值 ,让 表示从当前的 到最优值的步长,如下图所示。
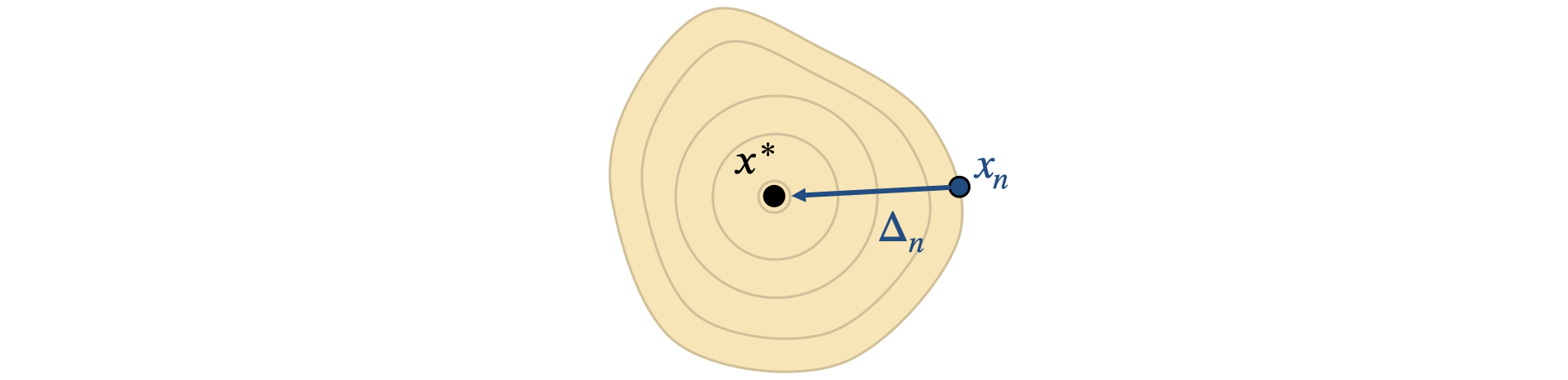
假设 可微分,我们可以在 处对 进行拉格朗日展开:
在第二行中,我们已经除以 ,并以缩短符号去掉了 和 。当我们把这一行插入 时,我们会得到
因此,与最优值的距离会因 的变化而改变,这意味着一旦我们足够接近最优值,就会出现二次收敛。这当然很好,但它仍然取决于前系数 ,如果前系数 就会发散。请注意,这是一个精确的表达式,由于拉格朗日展开的缘故,没有截断。到目前为止,我们已经实现了二次收敛,但并不能保证收敛到最优。为此,我们必须允许步长可变。
2.8.4 自适应步长
因此,作为牛顿法的下一步,我们引入了步长可变的,从而得到迭代 。如下图所示,如果 不完全是抛物线,而且小的 可能会以不理想的方式超调,那么这一点就特别有用。本例中最左侧的例子:
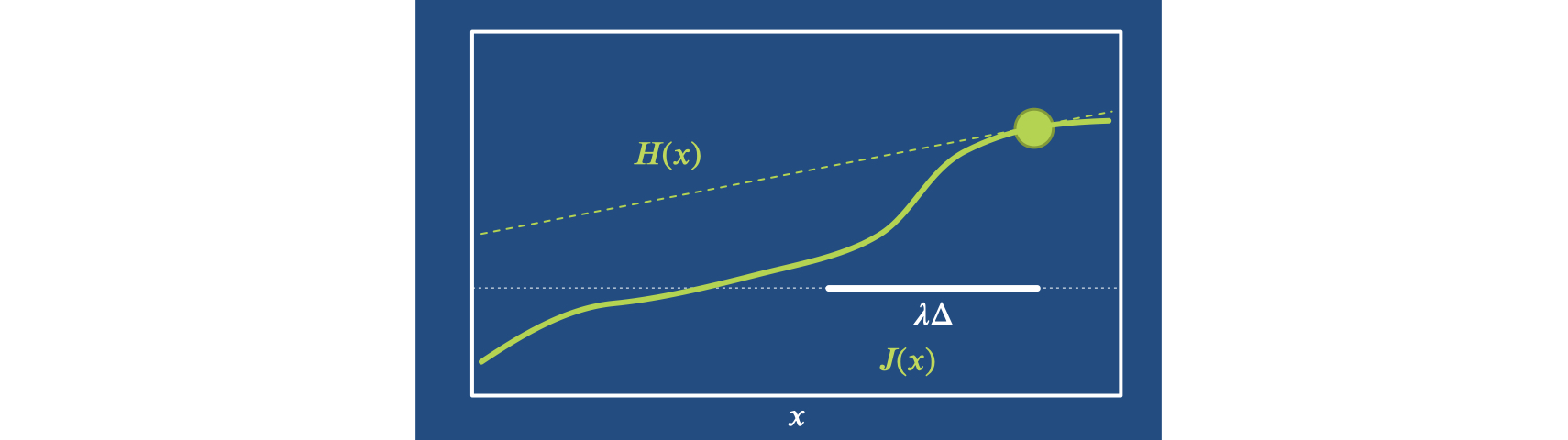
为了说明收敛性,我们需要一些基本假设:损失函数的凸性和平滑性。然后,我们将专注于证明损失会减少,并且我们会沿着一连串损失值较低的较小集合 移动。
首先, 我们对 应用基本定理:
类似地, 使用它围绕此位置表达 :
将这个 插入 中会产生:
在这里,我们首先使用了 ,然后把它移到第三行的积分中,与 项一起。第四行将 因数化。这样,我们就可以对上式(10)最后一行中的第一项 进行积分。
在接下来的一系列步骤中,我们将首先使用 。这一术语将简称为 。由于 的特性,这个 "只是 "代表一个小的正因子,它会一直存在到最后。之后,在下面的第 3 行和第 4 行中,我们可以开始寻找损失变化的上限。我们首先使用考希-施瓦茨不等式,然后利用仿射共轭矩阵的特殊 Lipschitz 条件。对于 ,它的形式是 。这就要求 是对称的正定式,这在实际中并不是太不合理。承上启下,我们可以得到:
由于 ,我们把 移到了第 2 行的积分内。在第 4 行中,除了应用特殊的 Lipschitz 条件外,我们尽可能地将 和 从积分中移出。最后三行只是简化术语,用 表示 的出现,并对积分进行评估。这样,我们就得到了以步长 为单位的三次方形式。最重要的是,第一个线性项是负的,因此对于较小的 将占主导地位。这样,我们就证明了对于足够小的 来说,步长将是负值:
然而,这本质上要求我们自由选择 ,因此该证明不适用于上述固定步长。它的一个很好的特性是,我们 "只 "要求 的 Lipschitz 连续性,而不是 或甚至 。
总之,我们已经证明,牛顿方法的自适应步长可以收敛,这非常好。然而,它需要 Hessian 作为核心要素。不幸的是, 在实践中很难获得。这是一个真正的拦路虎,也是以下方法的动因。这些方法保留了牛顿法的基本步骤,但对 进行了近似。
2.8.5 近似 Hessian
接下来, 我们将重新审视牛顿法导出的三种流行算法。
2.8.6 Broyden 方法
近似 的第一种方法是做一个非常粗略的猜测,即从特征矩阵 开始,然后通过有限差分近似迭代更新 。对于布洛伊登方法,我们使用向量除法 。
为了简化有限差分,我们另外假设在当前位置 时,已经达到 。当然,这并不一定正确,但在优化过程中,我们可以用下面这个简洁的表达式来修改 :
和之前一样,我们对 使用 的步长,分母来自有限差分 ,假设当前的雅各布值为零。请记住,这里的 是一个向量(见上文的向量分割),所以有限差分给出了一个大小为 的矩阵,可以添加到 。
Broyden 方法的优势在于我们无需计算全Hessian,而且可以高效地评估的更新。然而,上述两个假设使其成为一个非常粗糙的近似值,因此通过 中的逆Hessian对更新步骤进行归一化也相应地不可靠。
2.8.7 BFGS
这就产生了 BFGS 算法(以_Broyden-Fletcher-Goldfarb-Shanno_命名),它引入了一些重要的改进:它不假定 立即为零,并对更新的冗余部分进行补偿。这是必要的,因为有限差分 给出了 的完整近似值。我们可以尝试执行某种平均程序,但这会严重破坏 中的现有内容。因此,我们只沿着当前步长 减去 中的现有条目。这样做是有道理的,因为有限差分近似正好可以得到沿 的估计值。结合使用向量分割 ,这些变化给出了 的更新步长:
在实践中,BFGS 还利用直线搜索来确定步长 。由于 的大小较大,通常使用的 BFGS 变体也会使用 的缩小表示来节省内存。尽管如此,通过沿搜索方向的有限差分近似更新Hessian矩阵的核心步骤仍是 BFGS 的核心,并使其至少能部分补偿损失景观的缩放效应。目前,BFGS 变体是解决经典非线性优化问题最广泛使用的算法。
2.8.8 高斯牛顿法
通过限制 为经典的 损失,可以推导出牛顿法的另一个有吸引力的变体。这就是_高斯-牛顿(GN)算法。因此,我们仍然使用 ,但对于任意的 ,则依赖于 形式的平方损失。的导数用表示,而不是像之前那样用表示。由于链式规则,我们有 。
二阶导数得出以下表达式。为了简化 GN,我们省略了下面第二行中的二阶项:
在这里,一阶近似的剩余 项可以简化,这要归功于我们对 损失的关注: 和 。
等式 (13) 的最后一行意味着我们基本上是用 的平方来逼近 Hessian。这在很多情况下都是合理的,将其插入到我们上面的更新步骤中,就得到了高斯-牛顿更新 。
看这个更新, 它本质上采用了形式 的步骤, 即更新基于 的雅可比的逼近逆。这为所有参数提供了大致相等的步长, 作为这样的提供了我们将在本书后面重新审视的有趣构建块。以上形式意味着我们仍然必须求一个大矩阵的逆, 这代价高昂, 且矩阵本身可能甚至不可逆。
2.8.9 回到深度学习
上文我们已经说明,牛顿方法是许多流行的非线性优化算法的核心。现在,高斯-牛顿法终于为我们提供了通向深度学习算法的阶梯,特别是通向亚当优化器的阶梯。
2.8.10 Adam
像往常一样,我们从牛顿步骤 开始,但即使是高斯-牛顿对 的最简单近似,也需要求一个潜在的巨大矩阵的逆。这对于神经网络的权重来说是不可行的,因此一个合理的问题是,我们如何进一步简化这一步骤?对于Adam来说,答案就是:用对角线近似。具体来说,Adam使用:
这只是真正的Hessian的一个非常粗略的近似值。我们在这里使用的只是平方一阶导数,当然,一般来说,。这只适用于高斯-牛顿的一阶近似,即方程 (13) 的第一项。现在,亚当更进一步,只保留 的对角线。这个量在深度学习中以权重梯度的形式随时可用,并使 的反演变得微不足道。因此,它至少提供了对单个权重曲率的一些估计,但忽略了它们之间的相关性。
有趣的是,亚当并没有通过 进行完全反转,而是使用了分量平方根。这就有效地得到了 。因此,亚当沿着 移动,近似于在所有维度上执行一个固定大小的步长。
在实践中,Adam还引入了一些技巧,即计算梯度 以及梯度平方动量,在优化迭代过程中平均这两个量。这使得估算结果更加稳健,这一点至关重要:如果梯度输入错误地过小,那么归一化可能会导致爆炸。Adam 还在除法时增加了一个小常数,而平方根同样有助于减轻超调。
总而言之:Adam 利用一阶更新和对角高斯-牛顿近似赫塞斯进行归一化。此外,它还利用动量进行稳定。
2.8.11 梯度下降
为了实现梯度下降(GD)优化,我们现在采取最后一步,在 中假设 。这样,我们就有了一个由缩放梯度 组成的更新。
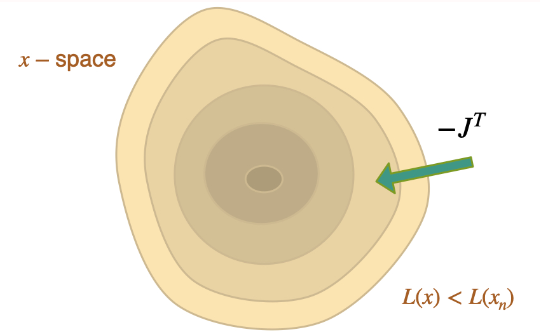
有趣的是,在没有任何形式的反转的情况下, 本身具有添加到 的正确形状,但它 "生活 "在错误的空间 中,而不是 本身。上述所有 "经典 "方案以某种形式使用的 与 本质上是不同的,这一事实就说明了这一点。缺乏反演步骤的问题在涉及物理学的问题中尤为突出,因此也是本章的重要启示之一。我们将在以后的 Scale-Invariance and Inversion中更详细地讨论这个问题。现在,我们建议大家牢记不同算法之间的关系,即使 "仅仅 "使用 Adam 或 GD。
最后,让我们来看看 GD 的收敛性。我们再次假设 具有凸性和可微性。用泰勒级数展开 的一步,用 Lipschitz 条件限定二阶项,我们得到
就像上面方程(11)中的牛顿方法一样,我们有一个负线性项,它在足够小的时支配着损失。结合起来,由于第一行中的 Lipschitz 条件,我们可以得到以下上界 .通过选择 ,我们可以进一步简化这些项,并得到一个取决于 平方的上界:,从而确保收敛。
遗憾的是,这一结果在实践中对我们帮助不大,因为在深度学习中,梯度的所有常见用法 都是未知的。不过,我们还是应该知道,梯度的 Lipschitz 常数在理论上可以为 GD 提供收敛保证。
至此,我们结束了经典优化器及其与深度学习方法的关系之旅。值得注意的是,为了清楚起见,我们在这里重点讨论了非随机算法,因为随机算法的证明会变得更加复杂。
有了这些背景知识,现在正是开始研究一些实际例子的好时机,这些例子从尽可能简单的开始,采用完全有监督的方法进行训练。
这里的监督(Supervised)主要是指:"用老办法做事"。当然,在深度学习(DL)的语境中,"老套"还是相当新的。此外,"老套"并不总是意味着不好--我们稍后将讨论训练网络的方法,这些方法明显优于使用监督训练的方法。
尽管如此,"监督训练 "是人们在 DL 背景下遇到的所有项目的起点,因此值得研究。此外,虽然 "监督训练 "的结果通常不如基于物理学的方法,但在某些应用场景中,如果没有好的模型方程,"监督训练 "可能是唯一的选择。
3.1 问题设置
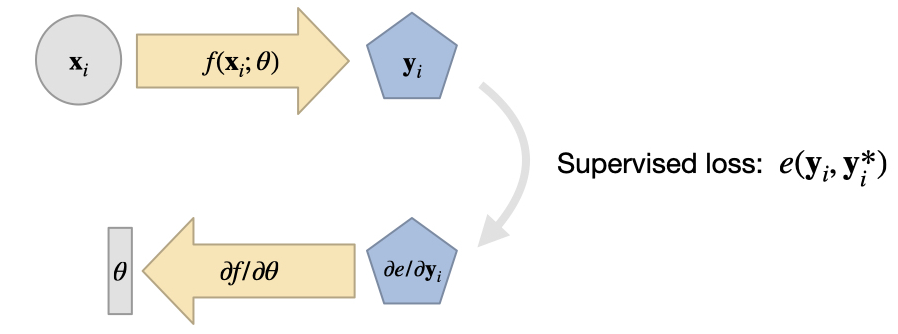
在监督训练中,我们面对一个未知函数 ,收集大量数据对 (训练数据集),并直接训练一个 NN 来表示 的近似值 。
我们用这种方法得到的 通常不是精确的,而是通过最小化问题得到的:通过调整表示 的 NN 的权重 ,使得
这样我们就能得到 ,从而在我们选择 和超参数进行训练的情况下,尽可能精确地得到 的结果。请注意,上面我们假设的是最简单的 损失。更一般的版本会在损失 中使用一个误差度量 ,通过 来最小化。关于合适度量的选择,我们稍后再讨论。
无论我们选择哪种度量方法,这一表述都给出了监督式方法的实际 "学习 "过程。
训练数据通常需要相当大的规模,因此使用数值模拟求解物理模型 来产生大量可靠的输入输出对进行训练是很有吸引力的。这意味着训练过程使用一组模型方程,并对其进行数值近似,以训练 NN 表示 。这样做有很多好处,例如,我们没有真实世界设备的测量噪声,也不需要人工标注大量样本来获取训练数据。
另一方面,这种方法也继承了以模拟代替实验的常见挑战:首先,我们需要确保所选模型有足够的能力来预测我们感兴趣的真实世界现象的行为。此外,数值近似会产生数值误差,需要将误差控制得足够小,以满足所选应用的需要。由于这些问题在经典模拟中都有深入研究,因此同样可以利用现有知识来设置 DL 训练任务。
3.2 代理模型
上述监督方法的核心优势之一是我们可以得到一个 代理模型(Surrogate Model),即一个模仿原始 行为的新函数。针对现实世界现象的 PDE 模型的数值近似通常计算成本很高。另一方面,训练有素的 NN 每次评估的成本是固定的,而且在 GPU 或 NN 单元等专用硬件上进行评估通常是微不足道的。
尽管如此,还是要小心谨慎:神经网络可以迅速产生大量介于两者之间的结果。考虑一个具有 特征的 CNN 层。如果我们将其应用于 的输入,即大约 16k 个单元,我们会得到 的中间值。这就超过了 200 万。所有这些值至少需要暂时存储在内存中,并由下一层进行处理。
尽管如此, 我们仍需谨慎: NN 可以快速生成大量中间结果。考虑一个具有 个特征的 CNN 层。如果我们将其应用于 ,即大约 16 k 个单元的输入, 我们会得到 个中间值。这已经超过了 200 万。这些值至少需要暂时存储在内存中,并由下一层处理。
然而,用快速、可学习的近似方法取代复杂、昂贵的求解器是一个非常有吸引力和有趣的方向。
3.3 给我看看代码!
最后,让我们来看一个训练神经网络的代码示例:我们将用[TWPH20]中的代用模型替换机翼周围湍流的完整求解器。
3.4 翼型周围 RANS 流动的监督训练
3.4.1 概述
在这个监督训练的例子中,我们有一个翼面周围的湍流气流,我们想知道在不同雷诺数和攻角下,该翼面周围的平均运动和压力分布。因此,在给定机翼形状、雷诺数和攻角的情况下,我们希望获得机翼周围的速度场和压力场。
经典的近似方法是_雷诺兹平均纳维-斯托克斯(RANS)模型,这种设置仍然是纳维-斯托克斯求解器在工业中最广泛的应用之一。不过,我们现在的目标不是依靠传统的数值方法来求解 RANS 方程,而是通过神经网络训练一个完全绕过数值求解器的代理模型,并以速度和压力的形式求解。
3.4.2 准备工作
根据监督模型的描述, 我们的学习任务非常简单直接, 可以写成
其中, 和 分别由一组物理场组成,而索引 则表示数据集所有离散点的差值。
我们的目标是在围绕翼面的计算域 中推断速度 和压力场 。作为输入,我们有雷诺数。在 中的雷诺数 、攻角 中的攻角 ,以及机翼形状 ,这些数据以 的栅格编码。 和 是以自由流流速 的形式提供的,其 x 和 y 分量表示为相同大小的常数域,在机翼区域包含零。因此,输入和输出具有相同的尺寸:。输入包含 ,而输出则存储通道 。这正是我们下面要为 NN 指定的输入和输出维度。
这里需要注意的一点是,我们在 中关注的量包含三个不同的物理场。虽然两个速度分量在本质上非常相似,但压力场通常具有与速度近似平方缩放的不同行为(参见 伯努利)。这意味着我们需要小心处理简单求和(如上文的最小化问题),并注意对数据进行归一化处理。
3.4.3 代码即将出现...
让我们开始实施吧。请注意,我们将跳过数据生成过程。下面的代码改变this codebase。在这里,我们只需下载一小部分在OpenFOAM中通过 Spalart-Almaras RANS 仿真生成的训练数据。
import numpy as np
import os.path, random
import torch
from torch.utils.data import Dataset
print("Torch version {}".format(torch.__version__))
# get training data
dir = "./"
if True:
# download
if not os.path.isfile('data-airfoils.npz'):
import requests
print("Downloading training data (300MB), this can take a few minutes the first time...")
with open("data-airfoils.npz", 'wb') as datafile:
resp = requests.get('https://dataserv.ub.tum.de/s/m1615239/download?path=%2F&files=dfp-data-400.npz', verify=False)
datafile.write(resp.content)
else:
# alternative: load from google drive (upload there beforehand):
from google.colab import drive
drive.mount('/content/gdrive')
dir = "./gdrive/My Drive/"
npfile=np.load(dir+'data-airfoils.npz')
print("Loaded data, {} training, {} validation samples".format(len(npfile["inputs"]),len(npfile["vinputs"])))
print("Size of the inputs array: "+format(npfile["inputs"].shape))
Torch version 2.0.1+cu118
Downloading training data (300MB), this can take a few minutes the first time...
Loaded data, 320 training, 80 validation samples
Size of the inputs array: (320, 3, 128, 128)
如果您在 colab 中运行本笔记本,上面的 else语句(默认情况下未激活)可能会对您有帮助:与其每次都重新下载训练数据,您可以手动下载一次并将其存储在谷歌硬盘中。我们假设它存储在根目录下,名为 data-airfoils.npz。之后,您可以使用上面的代码从谷歌硬盘加载文件,这样通常会快很多。如果您想通过 colab 进行更广泛的实验,强烈建议使用此方法。
3.4.4 RANS 训练数据
现在我们有了一些训练数据。一般来说,尽可能多地了解我们正在使用的数据是非常重要的(对于任何 ML 任务来说,garbage-in-gargabe-out 原则绝对成立)。我们至少应该从维度和粗略统计的角度来理解数据,最好还能从内容的角度来理解数据。否则,我们将很难解释训练运行的结果。而且,尽管有所有的 DL 魔法:如果你无法在数据中找出任何模式,NNs 肯定也找不到任何有用的模式。
因此,让我们来看看其中一个训练样本...下面只是一些辅助代码,用于并排显示图像。
import pylab
# helper to show three target channels: normalized, with colormap, side by side
def showSbs(a1,a2, stats=False, bottom="NN Output", top="Reference", title=None):
c=[]
for i in range(3):
b = np.flipud( np.concatenate((a2[i],a1[i]),axis=1).transpose())
min, mean, max = np.min(b), np.mean(b), np.max(b);
if stats: print("Stats %d: "%i + format([min,mean,max]))
b -= min; b /= (max-min)
c.append(b)
fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
axes.set_xticks([]); axes.set_yticks([]);
im = axes.imshow(np.concatenate(c,axis=1), origin='upper', cmap='magma')
pylab.colorbar(im); pylab.xlabel('p, ux, uy'); pylab.ylabel('%s %s'%(bottom,top))
if title is not None: pylab.title(title)
NUM=72
showSbs(npfile["inputs"][NUM],npfile["targets"][NUM], stats=False, bottom="Target Output", top="Inputs", title="3 inputs are shown at the top (free-ux, free-uy, mask), with the 3 output channels (p,ux,uy) at the bottom")

接下来,让我们定义一个小的辅助类 DfpDataset 来组织输入和目标。我们将把相应的数据传输到 pytorch 的 DataLoader类。
我们还设置了一些全局参数来控制训练参数,其中最重要的可能是:学习率 LR,即从上一次训练中获得的 。当训练运行没有收敛时,这是第一个需要实验的参数。
在这里,我们将始终保持相对较小的学习率。(使用学习率衰减会更好,即有可能改善收敛性,但为了清晰起见,此处省略)。
# some global training constants
# number of training epochs
EPOCHS = 100
# batch size
BATCH_SIZE = 10
# learning rate
LR = 0.00002
class DfpDataset():
def __init__(self, inputs,targets):
self.inputs = inputs
self.targets = targets
def __len__(self):
return len(self.inputs)
def __getitem__(self, idx):
return self.inputs[idx], self.targets[idx]
tdata = DfpDataset(npfile["inputs"],npfile["targets"])
vdata = DfpDataset(npfile["vinputs"],npfile["vtargets"])
trainLoader = torch.utils.data.DataLoader(tdata, batch_size=BATCH_SIZE, shuffle=True , drop_last=True)
valiLoader = torch.utils.data.DataLoader(vdata, batch_size=BATCH_SIZE, shuffle=False, drop_last=True)
print("Training & validation batches: {} , {}".format(len(trainLoader),len(valiLoader) ))
输出结果为:
Training & validation batches: 32 , 8
3.4.5 网络设置
现在我们可以设置神经网络的架构,我们将使用完全卷积 U-net。这是一种广泛使用的架构,使用不同空间分辨率的卷积堆叠。与普通卷积网络的主要区别在于,从编码器到解码器部分引入了skip connection。这可以确保在特征提取过程中不会丢失任何信息。(请注意,这只有在网络作为一个整体使用时才有效。例如,如果我们想将解码器作为一个独立的组件来使用,这就行不通了)。
下面是体系结构概述:
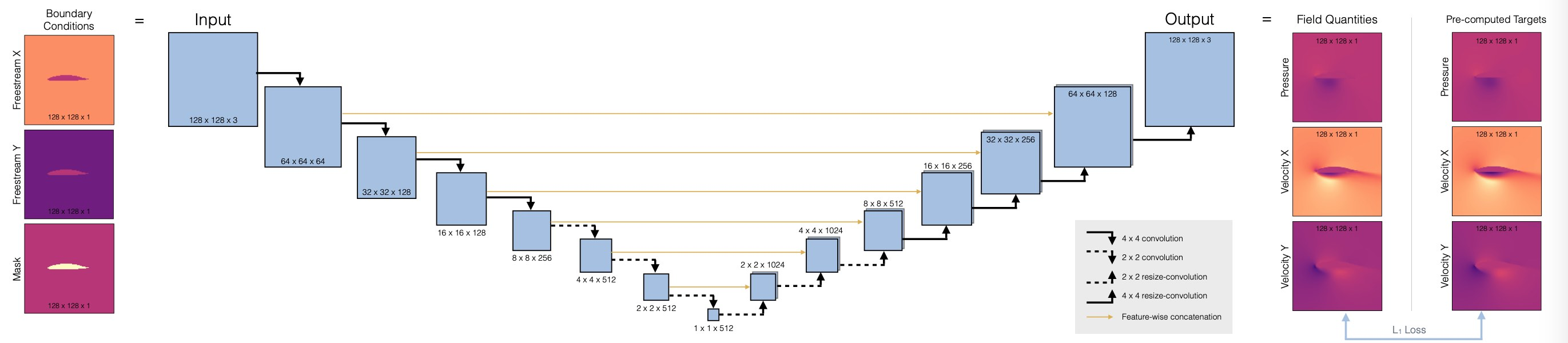
首先,我们将定义一个辅助程序,用于在网络中设置一个卷积块,即 blockUNet 。注意,我们不使用任何池化!相反,我们按照 最佳实践,使用跨距和转置卷积(解码器部分需要对称,即内核大小不均)。完整的 pytroch 神经网络通过 DfpNet 类进行管理。
import os, sys, random
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torch.autograd
import torch.utils.data
def blockUNet(in_c, out_c, name, size=4, pad=1, transposed=False, bn=True, activation=True, relu=True, dropout=0. ):
block = nn.Sequential()
if not transposed:
block.add_module('%s_conv' % name, nn.Conv2d(in_c, out_c, kernel_size=size, stride=2, padding=pad, bias=True))
else:
block.add_module('%s_upsam' % name, nn.Upsample(scale_factor=2, mode='bilinear'))
# reduce kernel size by one for the upsampling (ie decoder part)
block.add_module('%s_tconv' % name, nn.Conv2d(in_c, out_c, kernel_size=(size-1), stride=1, padding=pad, bias=True))
if bn:
block.add_module('%s_bn' % name, nn.BatchNorm2d(out_c))
if dropout>0.:
block.add_module('%s_dropout' % name, nn.Dropout2d( dropout, inplace=True))
if activation:
if relu:
block.add_module('%s_relu' % name, nn.ReLU(inplace=True))
else:
block.add_module('%s_leakyrelu' % name, nn.LeakyReLU(0.2, inplace=True))
return block
class DfpNet(nn.Module):
def __init__(self, channelExponent=6, dropout=0.):
super(DfpNet, self).__init__()
channels = int(2 ** channelExponent + 0.5)
self.layer1 = blockUNet(3 , channels*1, 'enc_layer1', transposed=False, bn=True, relu=False, dropout=dropout )
self.layer2 = blockUNet(channels , channels*2, 'enc_layer2', transposed=False, bn=True, relu=False, dropout=dropout )
self.layer3 = blockUNet(channels*2, channels*2, 'enc_layer3', transposed=False, bn=True, relu=False, dropout=dropout )
self.layer4 = blockUNet(channels*2, channels*4, 'enc_layer4', transposed=False, bn=True, relu=False, dropout=dropout )
self.layer5 = blockUNet(channels*4, channels*8, 'enc_layer5', transposed=False, bn=True, relu=False, dropout=dropout )
self.layer6 = blockUNet(channels*8, channels*8, 'enc_layer6', transposed=False, bn=True, relu=False, dropout=dropout , size=2,pad=0)
self.layer7 = blockUNet(channels*8, channels*8, 'enc_layer7', transposed=False, bn=True, relu=False, dropout=dropout , size=2,pad=0)
# note, kernel size is internally reduced by one for the decoder part
self.dlayer7 = blockUNet(channels*8, channels*8, 'dec_layer7', transposed=True, bn=True, relu=True, dropout=dropout , size=2,pad=0)
self.dlayer6 = blockUNet(channels*16,channels*8, 'dec_layer6', transposed=True, bn=True, relu=True, dropout=dropout , size=2,pad=0)
self.dlayer5 = blockUNet(channels*16,channels*4, 'dec_layer5', transposed=True, bn=True, relu=True, dropout=dropout )
self.dlayer4 = blockUNet(channels*8, channels*2, 'dec_layer4', transposed=True, bn=True, relu=True, dropout=dropout )
self.dlayer3 = blockUNet(channels*4, channels*2, 'dec_layer3', transposed=True, bn=True, relu=True, dropout=dropout )
self.dlayer2 = blockUNet(channels*4, channels , 'dec_layer2', transposed=True, bn=True, relu=True, dropout=dropout )
self.dlayer1 = blockUNet(channels*2, 3 , 'dec_layer1', transposed=True, bn=False, activation=False, dropout=dropout )
def forward(self, x):
# note, this Unet stack could be allocated with a loop, of course...
out1 = self.layer1(x)
out2 = self.layer2(out1)
out3 = self.layer3(out2)
out4 = self.layer4(out3)
out5 = self.layer5(out4)
out6 = self.layer6(out5)
out7 = self.layer7(out6)
# ... bottleneck ...
dout6 = self.dlayer7(out7)
dout6_out6 = torch.cat([dout6, out6], 1)
dout6 = self.dlayer6(dout6_out6)
dout6_out5 = torch.cat([dout6, out5], 1)
dout5 = self.dlayer5(dout6_out5)
dout5_out4 = torch.cat([dout5, out4], 1)
dout4 = self.dlayer4(dout5_out4)
dout4_out3 = torch.cat([dout4, out3], 1)
dout3 = self.dlayer3(dout4_out3)
dout3_out2 = torch.cat([dout3, out2], 1)
dout2 = self.dlayer2(dout3_out2)
dout2_out1 = torch.cat([dout2, out1], 1)
dout1 = self.dlayer1(dout2_out1)
return dout1
def weights_init(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
m.weight.data.normal_(0.0, 0.02)
elif classname.find('BatchNorm') != -1:
m.weight.data.normal_(1.0, 0.02)
m.bias.data.fill_(0)
接下来,我们可以初始化一个 DfpNet实例。
下面,EXPO参数控制着我们的 Unet 特征图的指数:这直接决定了网络的大小(3 可以使网络拥有约 15 万个参数)。这对于一个有 输出的生成式 NN 而言,这个参数相对较小,但训练时间很快,而且可以防止过度拟合,因为我们在这里使用的数据集相对较小。因此,这是一个很好的起点。
# channel exponent to control network size
EXPO = 3
# setup network
net = DfpNet(channelExponent=EXPO)
#print(net) # to double check the details...
nn_parameters = filter(lambda p: p.requires_grad, net.parameters())
params = sum([np.prod(p.size()) for p in nn_parameters])
# crucial parameter to keep in view: how many parameters do we have?
print("Trainable params: {} -> crucial! always keep in view... ".format(params))
net.apply(weights_init)
criterionL1 = nn.L1Loss()
optimizerG = optim.Adam(net.parameters(), lr=LR, betas=(0.5, 0.999), weight_decay=0.0)
targets = torch.autograd.Variable(torch.FloatTensor(BATCH_SIZE, 3, 128, 128))
inputs = torch.autograd.Variable(torch.FloatTensor(BATCH_SIZE, 3, 128, 128))
Trainable params: 147363 -> crucial! always keep in view...
指数为 3 时,该网络有 147555 个可训练参数。正如打印语句中的微妙提示所示,在训练 NN 时,这是一个需要时刻关注的关键数字。改变设置很容易得到一个拥有数百万个参数的网络,结果可能会出现各种收敛和过拟合问题。参数的数量肯定要与训练数据的数量相匹配,还应该与网络的深度成比例。不过,这三者之间的确切关系取决于问题的具体情况。
3.4.6 训练
最后,我们可以对 NN 进行训练。这一步可能要花费一些时间,因为训练会对所有 320 个样本运行 100 次,并不断评估验证样本,以跟踪 NN 的当前状态。
history_L1 = []
history_L1val = []
if os.path.isfile("network"):
print("Found existing network, loading & skipping training")
net.load_state_dict(torch.load("network")) # optionally, load existing network
else:
print("Training from scratch")
for epoch in range(EPOCHS):
net.train()
L1_accum = 0.0
for i, traindata in enumerate(trainLoader, 0):
inputs_curr, targets_curr = traindata
inputs.data.copy_(inputs_curr.float())
targets.data.copy_(targets_curr.float())
net.zero_grad()
gen_out = net(inputs)
lossL1 = criterionL1(gen_out, targets)
lossL1.backward()
optimizerG.step()
L1_accum += lossL1.item()
# validation
net.eval()
L1val_accum = 0.0
for i, validata in enumerate(valiLoader, 0):
inputs_curr, targets_curr = validata
inputs.data.copy_(inputs_curr.float())
targets.data.copy_(targets_curr.float())
outputs = net(inputs)
outputs_curr = outputs.data.cpu().numpy()
lossL1val = criterionL1(outputs, targets)
L1val_accum += lossL1val.item()
# data for graph plotting
history_L1.append( L1_accum / len(trainLoader) )
history_L1val.append( L1val_accum / len(valiLoader) )
if epoch<3 or epoch%20==0:
print( "Epoch: {}, L1 train: {:7.5f}, L1 vali: {:7.5f}".format(epoch, history_L1[-1], history_L1val[-1]) )
torch.save(net.state_dict(), "network" )
print("Training done, saved network")
程序输出结果为:
Training from scratch
Epoch: 0, L1 train: 0.29219, L1 vali: 0.23295
Epoch: 1, L1 train: 0.25406, L1 vali: 0.22507
Epoch: 2, L1 train: 0.22487, L1 vali: 0.21019
Epoch: 20, L1 train: 0.05228, L1 vali: 0.04134
Epoch: 40, L1 train: 0.03730, L1 vali: 0.03020
Epoch: 60, L1 train: 0.03236, L1 vali: 0.02523
Epoch: 80, L1 train: 0.03364, L1 vali: 0.02302
Training done, saved network
NN 终于训练完成!损失的绝对值应该已经很好地下降了:在标准设置下,验证损失的初始值约为 0.2,100 个epoch后约为 0.02。
让我们看看图表,直观地了解训练是如何随时间推移的。这对于识别训练的长期趋势非常重要。在实践中,很难发现命令行日志中 100 个左右的嘈杂数字的整体趋势是略微上升还是下降,而这在可视化中更容易发现。
import matplotlib.pyplot as plt
l1train = np.asarray(history_L1)
l1vali = np.asarray(history_L1val)
plt.plot(np.arange(l1train.shape[0]),l1train,'b',label='Training loss')
plt.plot(np.arange(l1vali.shape[0] ),l1vali ,'g',label='Validation loss')
plt.legend()
plt.show()
程序输出如下:
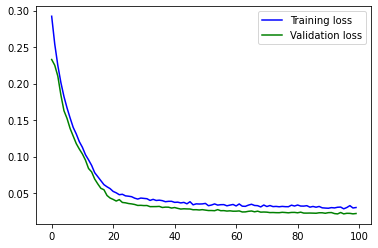
您应该看到一条曲线,它在大约 40 个epoch中一直在下降,然后开始变得平缓。在最后一部分,它仍在缓慢下降,最重要的是,验证损失并没有增加。这肯定是过度拟合的迹象,我们应该避免。(试着人为减少训练数据量,就能有意识地造成过度拟合)。
3.4.7 训练进度和验证
如果仔细观察这张图,你会发现一些奇怪的现象:为什么验证损失低于训练损失?
当然,这些数据与训练数据类似,但从某种程度上说,它们略微 "艰难 "一些,因为网络在训练过程中肯定从未收到过任何验证样本。验证损失略微偏离训练损失是很自然的,但对于这些输入,L1 损失怎么会更低?
这是由于上述训练循环在 pytorch 中的实现方式造成的:虽然训练损失是在训练模式下通过 net.train() 进行评估的,但评估是在调用 net.eval() 之后进行的。这将关闭批量归一化,并禁用 dropout(如果激活)等功能。这会稍微改变评估结果。代码还会运行一个训练步骤,根据网络在一个epoch中的演化状态来测量图中每个点的损失。更新网络后,再运行验证样本。因此,所有验证样本所使用的状态都与历时的初始状态略有不同(希望更好一些)。由于这两个原因,验证损失可能会有偏差,在本例中通常会略低一些。
这里需要提醒的是:永远不要用训练数据来评估你的网络!因为过度拟合是一个非常常见的问题。至少要使用网络从未见过的数据,即验证数据,如果看起来不错,再尝试一些不同的(至少稍微超出分布范围的)输入,即_测试数据_。下一个单元格将在验证数据上运行训练有素的网络,并使用 showSbs 函数显示其中一个数据。
net.eval()
for i, validata in enumerate(valiLoader, 0):
inputs_curr, targets_curr = validata
inputs.data.copy_(inputs_curr.float())
targets.data.copy_(targets_curr.float())
outputs = net(inputs)
outputs_curr = outputs.data.cpu().numpy()
if i<1: showSbs(targets_curr[0] , outputs_curr[0], title="Validation sample %d"%(i*BATCH_SIZE))
输出结果为:
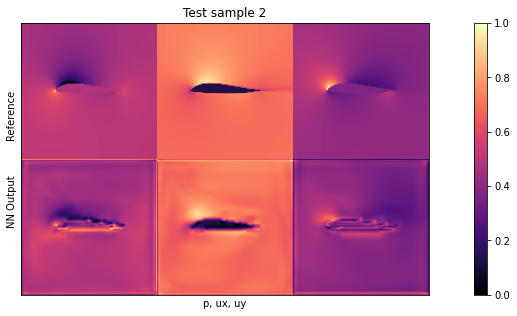
从外观上看,输入和网络输出之间至少应该有大致的相似之处。不过,我们还是留待测试数据时再进行更详细的评估吧。
3.4.8 测试评估
现在我们来看看实际的测试样本:在这种情况下,我们将使用新的机翼形状作为分布外(OOD)数据。这些形状是网络在任何训练样本中都从未见过的,因此它可以告诉我们网络对未见输入的泛化程度(验证数据不足以得出泛化结论)。
我们将使用与之前相同的可视化方式,正如伯努利方程所示,尤其是第一列中的_压力_对网络来说是一个具有挑战性的量。由于它与输入自由流速度和局部峰值呈立方比例关系,因此是网络最难推断的量。
下面的单元首先下载包含这些测试数据样本的较小档案,然后通过网络运行。评估循环还会计算累计 L1 误差,这样我们就可以量化网络在测试样本上的表现。
if not os.path.isfile('data-airfoils-test.npz'):
import urllib.request
url="https://physicsbaseddeeplearning.org/data/data_test.npz"
print("Downloading test data, this should be fast...")
urllib.request.urlretrieve(url, 'data-airfoils-test.npz')
nptfile=np.load('data-airfoils-test.npz')
print("Loaded {}/{} test samples\n".format(len(nptfile["test_inputs"]),len(nptfile["test_targets"])))
testdata = DfpDataset(nptfile["test_inputs"],nptfile["test_targets"])
testLoader = torch.utils.data.DataLoader(testdata, batch_size=1, shuffle=False, drop_last=True)
net.eval()
L1t_accum = 0.
for i, validata in enumerate(testLoader, 0):
inputs_curr, targets_curr = validata
inputs.data.copy_(inputs_curr.float())
targets.data.copy_(targets_curr.float())
outputs = net(inputs)
outputs_curr = outputs.data.cpu().numpy()
lossL1t = criterionL1(outputs, targets)
L1t_accum += lossL1t.item()
if i<3: showSbs(targets_curr[0] , outputs_curr[0], title="Test sample %d"%(i))
print("\nAverage test error: {}".format( L1t_accum/len(testLoader) ))
Downloading test data, this should be fast...
Loaded 10/10 test samples
Average test error: 0.028802116494625808
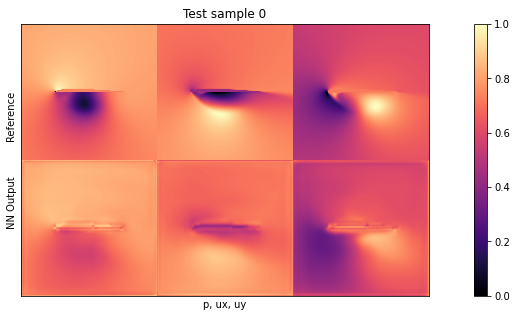
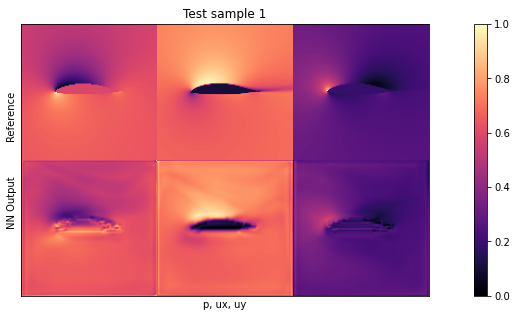
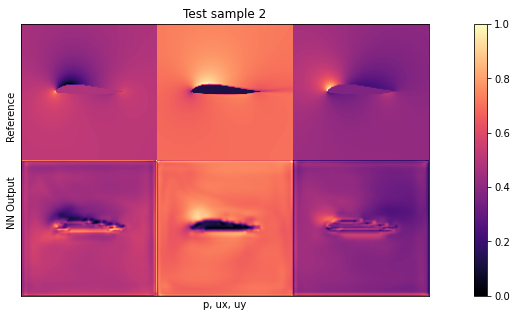
默认设置下的平均测试误差应约为 0.03。由于输入已归一化,这意味着所有三个字段的平均误差为每个量的最大值的 3%。这对于新形状来说不算太差,但显然还有改进的余地。
通过观察可视化效果,您会发现输出结果中缺少特别高的压力峰值和较大的 yvelocities 小区。这主要是由于网络太小,没有足够的资源来重建细节。
尽管如此,我们还是成功地用一个非常小而快速的神经网络架构取代了相当复杂的 RANS 求解器。它 "开箱即用"(通过 pytorch),支持 GPU,可微分,引入的误差仅为百分之几。通过额外的改动和更多的数据,这个设置可以变得非常精确[CT21]。
3.4.9 下一步
有很多显而易见的方法可以尝试(见下面的建议),例如延长训练时间、扩大数据集、扩大网络规模等。
- 试验学习率、辍学率和网络规模,以减少测试集上的误差。在给定训练数据的情况下,你能把误差减到多小?
- 述设置使用的是归一化数据。相反,你可以恢复撤销归一化后的原始场 来检查网络在原始数量上的表现。
- 正如你所看到的,在这里你能从这个数据集得到的东西有点有限,你可以去这个项目的主 github 仓库下载更大的数据集,或者生成自己的数据。
3.5 监督方法讨论
前面的例子说明,我们可以很容易地使用监督训练来解决复杂的任务。主要的工作量是收集足够大的示例数据集。一旦有了这些数据集,我们就可以训练一个网络来近似这些解法采样的解流形,训练好的网络可以很快给出预测结果。在使用监督训练时,有几个要点需要注意。

3.5.1 一些需要注意的事项...
3.5.1.1 自然出发点
监督训练 是任何 DL项目的自然起点。在这里,我们的意思是总是,从使用尽可能少的数据进行完全监督测试开始是有意义的。这将是一个纯粹的过拟合测试,但如果你的网络不能快速收敛并在单个示例上提供非常好的性能,那么你的代码或数据就存在根本性的问题。因此,我们没有理由继续进行更复杂的设置,因为这会增加发现这些基本问题的难度。
总结前几节的零散评论,这里有一套建立 DL 项目的 "黄金法则":
- 始终从 1 个样本的过拟合测试开始。- 检查网络有多少可训练参数。
- 缓慢增加训练数据量(以及可能的网络参数和深度)。
- 调整超参数(尤其是学习率)。
- 然后引入其他组件,如可变求解器或对抗训练。
3.5.1.2 稳定性
有监督训练的一个优点是非常稳定。当我们加入更复杂的物理模型或研究更复杂的 NN 架构时,情况也不会变得更好。
因此,在开始进行简单的过拟合测试时,请再次确保您能看到训练损失呈指数下降。这是一个很好的设置,可以找出作为最核心超参数的学习率的上限和合理范围。以后你可能还需要降低学习率,但至少应该能大致估算出 的合适值。
3.5.1.3 了解你的数据
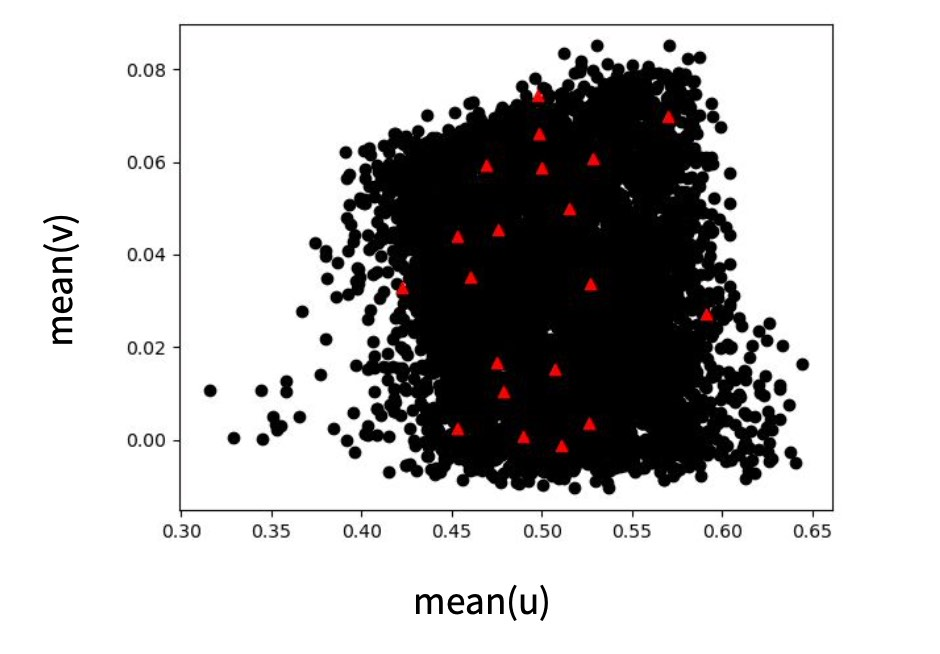
所有数据驱动型方法都遵循 "垃圾进垃圾出 "原则。因此,了解你所处理的数据非常重要。虽然没有放之四海而皆准的最佳方法,但我们强烈建议对数据集进行广泛的统计跟踪。一个好的起点是每个数量的平均值、标准偏差、最小值和最大值。如果其中某些值不正常,则表明数据集中存在不良样本。
这些值也可以很容易地通过直方图进行可视化,以追踪不需要的异常值。少量的异常值很容易使数据集出现偏差。
最后,检查不同数量之间的关系通常是个好主意,这样可以获得数据集所包含内容的一些直觉。下图给出了这一步骤的示例。
3.5.1.4 魔力在哪里?
在讨论 DL 方法时,尤其是在使用相对简单的训练方法时,你经常会听到这样的评论:"这不就是对数据进行插值吗?"
嗯,是的!这正是NN应该做的。从某种程度上说,没有其他事情可做。这就是所有 DL 方法的目的。它们为我们提供训练时所看到的数据的平滑表示。即使我们以后在训练时使用了花哨的物理模型,NN 也只是调整它们的权重来代表它们接收到的信号,并将其再现出来。
由于炒作和大量成功案例,不熟悉 DL 的人往往会产生这样的印象:DL 就像人类的大脑一样工作,能够从数据集中提取基本和一般原理("上帝的信息" 有人说过吗?)目前的技术水平并非如此。尽管如此,它仍是我们用来逼近复杂非线性函数的最强大工具。它是一个伟大的工具,但重要的是要记住,一旦我们正确设置了训练,我们从中得到的只是 NN 所训练的函数的近似值--不涉及任何魔法。
这意味着,你不应该指望网络能在它从未见过的数据上工作。从某种程度上说,神经网络之所以如此出色,正是因为它们能够准确地适应训练时接收到的信号,但与其他学习到的表征相比,神经网络实际上并不擅长外推。因此,我们不能指望神经网络能神奇地处理新的输入。相反,我们需要确保能够正确塑造输入空间,例如,通过归一化和关注不变量。
举个更具体的例子:如果您总是在的范围内训练您的网络输入,那么就不要指望它能在的输入下工作。在某些情况下,可以通过减去平均值来对输入和输出进行归一化,并通过标准偏差或合适的量化值进行归一化(确保这不会破坏数据中的重要相关性)。
经验法则:确保在实际训练 NN 时,输入尽可能与推理时要使用的输入相似。
这一点在接下来的章节中必须牢记:例如,如果我们希望 NN 与特定的模拟环境结合使用,那么在训练过程中就必须实际加入模拟器。否则,网络可能会专门处理预先计算的数据,而这些数据与将 NN 与求解器结合时产生的数据不同,即会出现_分布偏移_。
3.1.5.5 网格和栅格
前面的翼型示例使用了带有标准卷积的笛卡尔网格。就性能和稳定性而言,这些通常是最划算的。尽管如此,这里的整个讨论当然也适用于其他类型的卷积,例如,与图卷积结合的不太规则的网格,或具有连续卷积的基于粒子的数据(参见[非结构化网格和无网格方法](http://physicsbaseddeeplearning.org/others lagrangian.html))。当切换到这些方法时,你通常会看到学习性能降低,以换取采样灵活性的提高。 最后,关于全连接层或一般的MLP:我们建议尽可能避免这些。对于任何结构化数据,如空间函数或一般的字段数据,卷积是优选的,并且不太可能过拟合。例如,你会注意到细胞神经网络通常不需要丢弃,因为它们通过构建很好地正则化了。对于MLP,您通常需要相当多的方法来避免过拟合。

3.5.2 监督训练简述
总之,监督训练具有以下特点。
✅ 优点:
- 训练速度非常快。
- 稳定简单。
- 是一个很好的起点。
❌ 缺点:需要大量数据。
- 性能、准确性和泛化能力不够优秀。
- 与外部“进程”(如嵌入到求解器中)的交互困难。
接下来的章节将解释如何缓解监督训练的这些缺点。首先,我们将通过软约束将模型方程引入图像中,然后我们将重新审视将数值模拟和学习方法结合起来所面临的挑战。
前几节中的有监督设置可以通过相当简单的训练过程快速获得近似解。然而,令人痛心的是,我们只是将物理模型和数值方法作为一种 "外部 "工具,来产生一大堆数据。我们人类拥有大量关于如何用数学方法描述物理过程的知识。正如以下几章所展示的,我们可以通过人类的物理知识来指导训练过程,从而改进训练过程。

4.1 使用物理模型
给定一个具有时间演化的 的 PDE,我们通常可以用 的导数函数来表示,方法是
其中 的下标表示相对于一个空间维度的高阶空间导数(当然也可以包括相对于不同坐标轴的混合导数)。 表示随时间的变化。
在这种情况下,我们可以用神经网络来近似未知的 本身。如果近似值(我们称之为 )是准确的,那么 PDE 应该自然满足。换句话说,残差 R 应该等于零:
这与训练神经网络的目标很好地结合在一起:我们可以结合直接损失项来训练最小化残差。与之前类似,除了残差项之外,我们还可以使用预先计算出的解 ,将 与 作为约束条件。这一点通常很重要,因为除非指定初始条件和边界条件,否则大多数实际的 PDE 都没有唯一解。因此,如果我们只考虑 ,可能会得到带有随机偏移或其他不理想成分的解。因此,监督采样点有助于在某些地方固定解。
现在我们的训练目标变成了:
其中, 表示超参数,分别缩放监督项和残差项的贡献。当然,我们还可以在此添加适当比例系数的附加残差项。
注意方程(1)中两个不同项的含义很有启发:第一项是传统的、有监督的 L2 损失。如果我们只对这一损失进行优化,我们的网络就能很好地学习近似训练样本,但可能会在解中平均出多种模式,在样本点之间的区域表现不佳。相反,如果我们只优化第二项(物理残差),我们的神经网络可能会在局部满足 PDE,但产生的解仍可能与训练数据相去甚远。出现这种情况的原因可能是解中存在 "空位",即不同的解均满足残差。因此,我们要同时优化这两个目标,以便在最佳情况下,网络在学习近似训练数据的特定解的同时,还能捕捉到底层 PDE 的知识。
需要注意的是,与用于监督训练的数据样本类似,我们无法保证残差项 在训练过程中实际为零。训练过程的非线性优化将尽可能减少监督项和残差项,但这并不能保证。仍有可能存在大量非零残差项。我们将在接下来的代码示例中更详细地讨论这个问题,现在重要的是要记住,这种方式的物理约束只代表_软约束_,并不能保证最大限度地减少这些约束。
前面的概述并没有明确说明神经网络是如何产生 的。在这里,我们可以区分两种不同的方法:通过选择目标函数的显式表示(下文中的 v1),或通过使用全连接神经网络来表示解(v2)。例如,对于 v1,我们可以设置一个空间网格(或图形,或一组样本点),而在第二种情况下,不存在显式表示,而是由神经网络接收空间坐标,在查询位置生成解。下面我们将详细介绍这两种变体。
4.2 变体 1: 用于显式表示的残差导数
对于变式 1,我们选择离散化,并建立一个覆盖目标域的计算网格。在不失一般性的前提下,我们假设这是一个笛卡尔网格,以 的位置对空间进行采样。现在,训练一个 NN 来生成网格上的解:。对于规则网格,CNN 将是 的最佳选择,而对于三角形网格,我们可以使用图网络,或使用点演算的粒子网络。
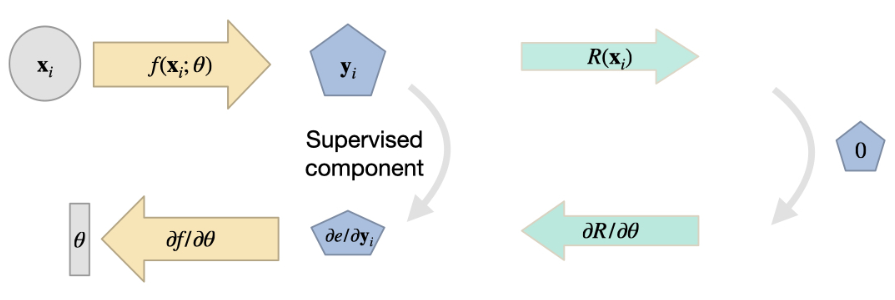
现在,我们可以在计算网格上将 的方程离散化,并用我们选择的方法计算导数。唯一需要注意的是:为了将残差纳入训练,我们必须制定评估方法,使深度学习框架可以通过计算进行反向传播。由于我们的网络 产生了解 ,而残差取决于它(),因此我们至少需要 ,这样才能对权重 进行梯度反向传播。幸运的是,如果我们用 DL 框架的操作来表示 ,那么该框架的反向传播功能就能解决这个问题。
这种变体在DL中有着相当悠久的 "传统",例如,Tompson et al. [TSSP17]很早就提出了这种变体来学习无散度运动。举个具体例子:如果我们的目标是学习无散度的速度 ,我们就可以使用这种训练方法来训练 NN,而无需预先计算无发散速度场作为训练数据。为了简洁起见,我们在这里将去掉空间指数(),并将重点放在上,我们同样可以将其简化:无散度必须在任何时候都保持不变,因此我们可以考虑从开始的单一步骤,即从有散度的到无散度的的归一化步骤。对于正常求解器,我们必须计算一个压力 ,使得 。这就是著名的矢量微积分基本定理,或Helmholtz decomposition,把矢量场分成_solenoidal_(无散度)和非旋转部分(压力梯度)。
为了学习这种分解,我们可以在计算网格上用 CNN 近似计算 :。学习目标变成最小化 的发散,也就是最小化 。为了实现这个残差,我们只需在计算网格上提供 的发散算子 即可。这通常可以通过 DL 框架中的卷积层轻松实现,该卷积层包含发散的有限差分权重。非常好的是,在这种情况下,我们甚至不需要额外的监督样本,通常只需使用这种残差公式进行训练即可。另外,与下面的变式 2 不同,我们可以直接处理相当大的解空间(我们并不局限于学习单个解)。我们可以在 代码库 中找到一个实现示例。
总的来说,变式 1 与可微分物理训练有很多共同之处(它基本上是一个子集)。由于我们将在 Introduction to Differentiable Physics和之后的文章中更详细地讨论可微分物理,从现在起,我们将专注于直接 NN 表示(变体 2)。
4.3 变体 2: 来自神经网络表示的导数
采用物理残差作为软约束的第二种变体是使用全连接的 NN 来表示 。这种_physics-infformed_方法由 Raissi 等人推广[RPK19],它有一些有趣的优点和缺点,我们将在下文中概述。在下面的代码示例和讨论中,我们将以物理信息版本(变体 2)为目标。
这里的中心思想是,我们在学习问题中所追求的上述通用函数 也可以用来获得物理场的表示,例如,满足 的场 。这意味着 将转化为 ,其中我们选择的 NN 参数 可以尽可能精确地表示出所需的 。
这种观点的一个很好的副作用是,NN 表征本质上支持导数的计算。导数 是通过梯度下降进行学习的关键基石,这在 Overview 中已有解释。现在,我们可以用同样的工具来计算空间导数,比如 ,注意,上面对于 ,我们把这个导数写成了简写符号 。对于随时间变化的函数,这当然也适用于 ,即上面符号中的 。
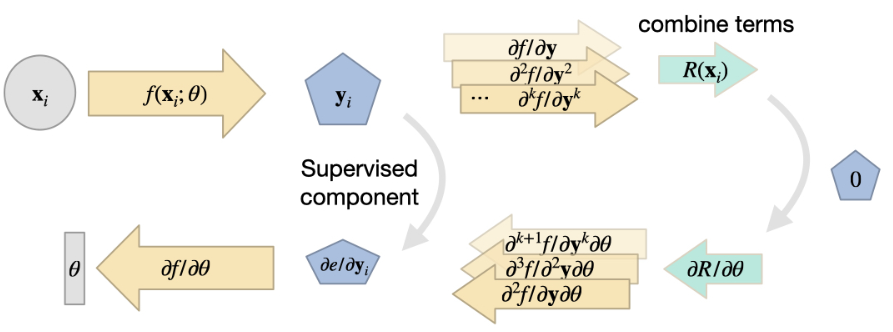
因此,对于由和项组成的通用,一旦我们有了代表的NN,我们就可以依靠DL框架的反向传播算法来计算这些导数。从本质上讲,这给我们提供了一个函数(NN),该函数接收空间和时间坐标来生成 的解。因此,输入通常是相当低维的,例如三维情况下随时间变化的 3+1 个值,通常会产生一个标量值或空间向量。由于缺乏明确的空间采样点,这里选择了 MLP(即全连接 NN)架构。
举个简单的例子,一维Burgers方程, ,我们可以直接提出一个损失项 ,在训练时应尽可能将其最小化。对于每个项,例如 ,我们可以简单地查询实现 的 DL 框架,以获得相应的导数。对于高阶导数,例如 ,我们可以简单地多次查询框架的导函数。在下一节中,我们将举例说明如何在 tensorflow 中实现这一功能。
4.4 到目前为止的总结
上述方法为我们提供了一种将物理方程作为软约束纳入 DL 学习的方法:残差损失。通常情况下,这种设置适用于逆问题,即我们想要找到一个 PDE 解的某些测量或观测结果。由于重构的成本很高(将在下文中演示),解流形不应该过于复杂。例如,仅使用物理残余损失通常无法捕捉到广泛的解,如之前的监督机翼示例。
为了说明物理信息损失是如何在变体 2 中发挥作用的,让我们以重建任务作为反问题的例子。我们将使用Burgers方程 作为一个简单但非线性的一维方程,我们在时间 时有一系列_观测值_。解应该符合Burgers方程的残差公式,并与观测结果相匹配。此外,让我们在计算域两侧施加狄利克雷边界条件 ,并将解定义在时间区间 上。
请注意,与之前的正向模拟示例类似,我们仍将使用 128 个点()对解进行采样,但现在我们通过 NN 进行了离散化。因此,我们也可以对中间的点进行采样,而无需明确选择用于插值的基函数。现在通过 NN 进行离散化,可以在内部决定如何使用其自由度来安排激活函数作为基函数。因此,我们无法直接控制重构。
5.1 原理
根据 2.5 模型与方程和前一节中的 符号,这个重构问题意味着我们要求解的是:
其中 表示时空点 ,参考解为 ,索引 表示数据集的不同采样点。 和 都表示 在空间和时间的不同位置的解,由于我们处理的是一维速度,所以 。在这个例子中, 表示布尔格斯方程 的参考值 ,在所有选定的时空点 上, 应尽可能接近这个参考值。
上述第一项是 "监督 "数据项,第二项表示残差函数 。它收集了及其导数的额外评估,以计算的残差。这种方法--使用神经网络的导数来计算PDE残差--通常被称为_physics-informed_方法,产生一个physics-informed神经网络(PINN)[RPK19] 来表示逆重建问题的解。
上述残差函数收集及其导数的其他评估值以构建的残差。这种方法——使用神经网络的导数来计算PDE残差——通常称为物理信息(physicals-informed)方法,产生一个物理信息神经网络(PINN)来表示反演重构问题的解。
因此,在上述公式中, 应简单地收敛为零。为简单起见,我们省略了目标函数中的缩放因子。请注意,实际上我们在这里处理的只是 的单个解 的单点样本。
5.2 准备工作
现在我们先用 tensorflow 后端加载 phiflow,然后初始化随机采样。(注:本例使用的是旧版本 1.5.1 的 phiflow)。
!pip install --quiet phiflow==1.5.1
from phi.tf.flow import *
import numpy as np
#rnd = TF_BACKEND # for phiflow: sample different points in the domain each iteration
rnd = math.choose_backend(1) # use same random points for all iterations
注:在python3.9之后,优于collections.Iterable被废弃,第7行语句会报错。这里需要打开文件C:\ProgramData\anaconda3\Lib\site-packages\phi\backend\scipy_backend.py,修改第37行为
if isinstance(values, collections.abc.Iterable):,注意重启内核。
我们在这里导入了 phiflow,但不会像Simple Forward Simulation of Burgers Equation with phiflow中那样用它来计算 PDE 的解。相反,我们将使用 NN 的导数(如上一节所述)来为训练设置损失公式。
接下来,我们建立了一个简单的NN,其中包含8个完全连接的层和每个20个单元的tanh激活。
我们还将定义 boundary_tx 函数和 open_boundary 函数,前者给出解的约束条件数组(本例中所有约束条件均为 ),后者存储 为 0 的约束条件。
def network(x, t):
""" Dense neural network with 8 hidden layers and 3021 parameters in total.
Parameters will only be allocated once (auto reuse).
"""
y = math.stack([x, t], axis=-1)
for i in range(8):
y = tf.layers.dense(y, 20, activation=tf.math.tanh, name='layer%d' % i, reuse=tf.AUTO_REUSE)
return tf.layers.dense(y, 1, activation=None, name='layer_out', reuse=tf.AUTO_REUSE)
def boundary_tx(N):
x = np.linspace(-1,1,128)
# precomputed solution from forward simulation:
u = np.asarray( [0.008612174447657694, 0.02584669669548606, 0.043136357266407785, 0.060491074685516746, 0.07793926183951633, 0.0954779141740818, 0.11311894389663882, 0.1308497114054023, 0.14867023658641343, 0.1665634396808965, 0.18452263429574314, 0.20253084411376132, 0.22057828799835133, 0.23865132431365316, 0.25673879161339097, 0.27483167307082423, 0.2929182325574904, 0.3109944766354339, 0.3290477753208284, 0.34707880794585116, 0.36507311960102307, 0.38303584302507954, 0.40094962955534186, 0.4188235294008765, 0.4366357052408043, 0.45439856841363885, 0.4720845505219581, 0.4897081943759776, 0.5072391070000235, 0.5247011051514834, 0.542067187709797, 0.5593576751669057, 0.5765465453632126, 0.5936507311857876, 0.6106452944663003, 0.6275435911624945, 0.6443221318186165, 0.6609900633731869, 0.67752574922899, 0.6939334022562877, 0.7101938106059631, 0.7263049537163667, 0.7422506131457406, 0.7580207366534812, 0.7736033721649875, 0.7889776974379873, 0.8041371279965555, 0.8190465276590387, 0.8337064887158392, 0.8480617965162781, 0.8621229412131242, 0.8758057344502199, 0.8891341984763013, 0.9019806505391214, 0.9143881632159129, 0.9261597966464793, 0.9373647624856912, 0.9476871303793314, 0.9572273019669029, 0.9654367940878237, 0.9724097482283165, 0.9767381835635638, 0.9669484658390122, 0.659083299684951, -0.659083180712816, -0.9669485121167052, -0.9767382069792288, -0.9724097635533602, -0.9654367970450167, -0.9572273263645859, -0.9476871280825523, -0.9373647681120841, -0.9261598056102645, -0.9143881718456056, -0.9019807055316369, -0.8891341634240081, -0.8758057205293912, -0.8621229450911845, -0.8480618138204272, -0.833706571569058, -0.8190466131476127, -0.8041372124868691, -0.7889777195422356, -0.7736033858767385, -0.758020740007683, -0.7422507481169578, -0.7263049162371344, -0.7101938950789042, -0.6939334061553678, -0.677525822052029, -0.6609901538934517, -0.6443222327338847, -0.6275436932970322, -0.6106454472814152, -0.5936507836778451, -0.5765466491708988, -0.5593578078967361, -0.5420672759411125, -0.5247011730988912, -0.5072391580614087, -0.4897082914472909, -0.47208460952428394, -0.4543985995006753, -0.4366355580500639, -0.41882350871539187, -0.40094955631843376, -0.38303594105786365, -0.36507302109186685, -0.3470786936847069, -0.3290476440540586, -0.31099441589505206, -0.2929180880304103, -0.27483158663081614, -0.2567388003912687, -0.2386513127155433, -0.22057831776499126, -0.20253089403524566, -0.18452269630486776, -0.1665634500729787, -0.14867027528284874, -0.13084990929476334, -0.1131191325854089, -0.09547794429803691, -0.07793928430794522, -0.06049114408297565, -0.0431364527809777, -0.025846763281087953, -0.00861212501518312] );
t = np.asarray(rnd.ones_like(x)) * 0.5
perm = np.random.permutation(128)
return (x[perm])[0:N], (t[perm])[0:N], (u[perm])[0:N]
def _ALT_t0(N): # alternative, impose original initial state at t=0
x = rnd.random_uniform([N], -1, 1)
t = rnd.zeros_like(x)
u = - math.sin(np.pi * x)
return x, t, u
def open_boundary(N):
t = rnd.random_uniform([N], 0, 1)
x = math.concat([math.zeros([N//2]) + 1, math.zeros([N//2]) - 1], axis=0)
u = math.zeros([N])
return x, t, u
最重要的是,我们现在还可以构建我们希望最小化的残差损失函数f,以便引导 NN 为我们的模型方程获取一个解。从最上面的方程中可以看出,我们需要与 、 相关的导数以及 的二次导数。下面 f 的前三行就是这样做的。
之后,我们只需将导数结合起来,就能形成Burgers方程。这里我们使用 phiflow 的 gradient函数:
def f(u, x, t):
""" Physics-based loss function with Burgers equation """
u_t = gradients(u, t)
u_x = gradients(u, x)
u_xx = gradients(u_x, x)
return u_t + u*u_x - (0.01 / np.pi) * u_xx
接下来,让我们在内域中设置采样点,以便将解与之前在 phiflow 中进行的正向模拟进行比较。
下面的单元格分配两个张量:grid_x将使用128个单元覆盖我们的域,即-1到1的范围,而grid_t将使用33个时间点对时间区间进行采样。
最后的math.expand_dims()调用只是添加了一个batch维度,这样得到的张量与下面的示例兼容。
N=128
grids_xt = np.meshgrid(np.linspace(-1, 1, N), np.linspace(0, 1, 33), indexing='ij')
grid_x, grid_t = [tf.convert_to_tensor(t, tf.float32) for t in grids_xt]
# create 4D tensor with batch and channel dimensions in addition to space and time
# in this case gives shape=(1, N, 33, 1)
grid_u = math.expand_dims(network(grid_x, grid_t))
现在,grid_u包含一个完整的图,用于在个位置上评估我们的NN,一旦我们通过session.run运行它,就会以数组的形式返回结果。让我们试一试:我们可以初始化一个 TF 会话,评估 grid_u 并将其显示在图像中,就像我们之前计算的 phiflow 解一样。
(注意,我们将使用Simple Forward Simulation of Burgers Equation with phiflow中的 show_state。因此,X 轴并不显示实际的模拟时间,而是显示被放大16倍的32个时间步,以使图像中随时间变化更容易看到。)
import pylab as plt
print("Size of grid_u: "+format(grid_u.shape))
session = Session(None)
session.initialize_variables()
def show_state(a, title):
for i in range(4): a = np.concatenate( [a,a] , axis=3)
a = np.reshape( a, [a.shape[1],a.shape[2]*a.shape[3]] )
fig, axes = plt.subplots(1, 1, figsize=(16, 5))
im = axes.imshow(a, origin='upper', cmap='inferno')
plt.colorbar(im) ; plt.xlabel('time'); plt.ylabel('x'); plt.title(title)
print("Randomly initialized network state:")
show_state(session.run(grid_u),"Uninitialized NN")
运行输出为:
Size of grid_u: (1, 128, 33, 1)
Randomly initialized network state:

这种可视化效果已经显示出空间和时间上的平滑过渡。到目前为止,这纯粹是我们正在采样的 NN 的随机初始化。因此,到目前为止,它与我们基于 PDE 模型的解决方案毫无关系。接下来的步骤将根据数据(来自boundary函数)和来自f的模型约束条件对约束条件进行实际评估,以获取 PDE 的实际解。
5.3 损失函数和训练
作为学习过程的目标,我们现在可以将direct 约束条件,即 时的解和狄利克雷 边界条件与来自 PDE 残差的损失结合起来。对于这两个边界约束条件,我们将在下方使用 100 个点,然后在内部区域使用额外的 1000 个点对解进行采样。
直接约束通过 network(x, t)[:, 0] - u 进行评估,其中 x 和 t 是我们希望对解进行采样的时空位置,而 u 则提供相应的真值。
对于物理损失点,我们没有真值解,但我们只需通过 NN 导数评估 PDE 残差,看看解是否满足 PDE 模型。如果不满足,就会直接产生误差,需要在优化过程中通过更新步骤来减少误差。相应的表达式如下f(network(x, t)[:, 0], x, t)。请注意,对于数据和物理项,network()[:, 0]表达式不会从 评估中删除任何数据,它们只是丢弃了网络返回的 张量的最后一个 size-1 维。
# Boundary loss
N_SAMPLE_POINTS_BND = 100
x_bc, t_bc, u_bc = [math.concat([v_t0, v_x], axis=0) for v_t0, v_x in zip(boundary_tx(N_SAMPLE_POINTS_BND), open_boundary(N_SAMPLE_POINTS_BND))]
x_bc, t_bc, u_bc = np.asarray(x_bc,dtype=np.float32), np.asarray(t_bc,dtype=np.float32) ,np.asarray(u_bc,dtype=np.float32)
#with app.model_scope():
loss_u = math.l2_loss(network(x_bc, t_bc)[:, 0] - u_bc) # normalizes by first dimension, N_bc
# Physics loss inside of domain
N_SAMPLE_POINTS_INNER = 1000
x_ph, t_ph = tf.convert_to_tensor(rnd.random_uniform([N_SAMPLE_POINTS_INNER], -1, 1)), tf.convert_to_tensor(rnd.random_uniform([N_SAMPLE_POINTS_INNER], 0, 1))
loss_ph = math.l2_loss(f(network(x_ph, t_ph)[:, 0], x_ph, t_ph)) # normalizes by first dimension, N_ph
# Combine
ph_factor = 1.
loss = loss_u + ph_factor * loss_ph # allows us to control the relative influence of loss_ph
optim = tf.train.GradientDescentOptimizer(learning_rate=0.02).minimize(loss)
#optim = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss) # alternative, but not much benefit here
上面的代码只是初始化了损失的评估,我们仍然没有进行任何优化步骤,但我们终于可以开始着手处理这个问题了。
尽管方程很简单,但收敛速度通常很慢。迭代本身的计算速度很快,但这种设置需要大量的迭代。为了将运行时间控制在合理范围内,我们默认只进行 10k 次迭代 (ITERS)。你可以增加这个值,以获得更好的结果。
session.initialize_variables()
import time
start = time.time()
ITERS = 10000
for optim_step in range(ITERS+1):
_, loss_value = session.run([optim, loss])
if optim_step<3 or optim_step%1000==0:
print('Step %d, loss: %f' % (optim_step,loss_value))
#show_state(grid_u)
end = time.time()
print("Runtime {:.2f}s".format(end-start))
Step 0, loss: 0.276599
Step 1, loss: 0.155847
Step 2, loss: 0.125085
Step 1000, loss: 0.053451
Step 2000, loss: 0.050352
Step 3000, loss: 0.047439
Step 4000, loss: 0.045276
Step 5000, loss: 0.042576
Step 6000, loss: 0.040332
Step 7000, loss: 0.036957
Step 8000, loss: 0.031184
Step 9000, loss: 0.028826
Step 10000, loss: 0.027606
Runtime 33.19
训练可能需要相当长的时间,在典型的notebook上大约需要2分钟,但至少误差显著下降(从约0.2降低到约0.03),网络似乎成功地收敛到一个解。
让我们通过在规则网格的中心评估网络来显示网络的重构,这样我们就可以将解显示为图像。请注意,这实际上相当昂贵,我们必须对所有的个采样点运行整个网络及其几千个权重。
不过,乍一看它看起来相当不错。与上面显示的随机初始化相比,发生了非常明显的变化:
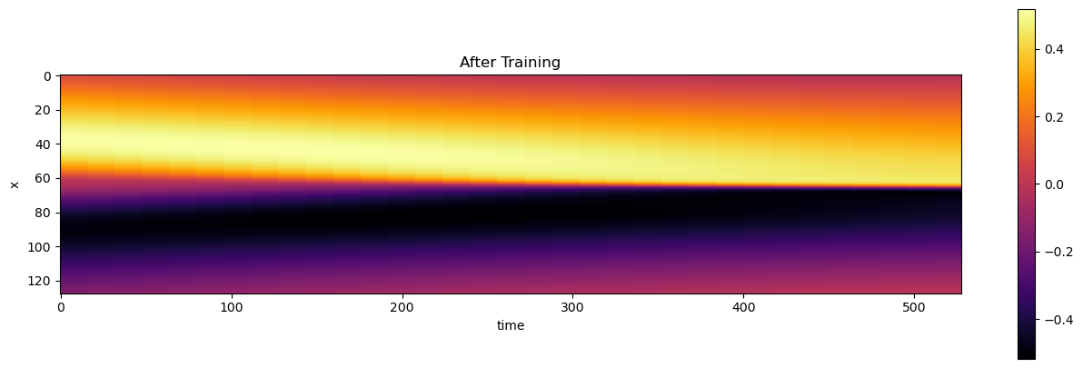
5.4 评估
让我们更详细地比较一下解法。下面是用于约束解法的实际样本点(时间步长为 16,)(灰色)和重构解法(蓝色):
u = session.run(grid_u)
# solution is imposed at t=1/2 , which is 16 in the array
BC_TX = 16
uT = u[0,:,BC_TX,0]
fig = plt.figure().gca()
fig.plot(np.linspace(-1,1,len(uT)), uT, lw=2, color='blue', label="NN")
fig.scatter(x_bc[0:100], u_bc[0:100], color='gray', label="Reference")
plt.title("Comparison at t=1/2")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()
反馈结果为:
<matplotlib.legend.Legend at 0x7f8eca2a7a00>
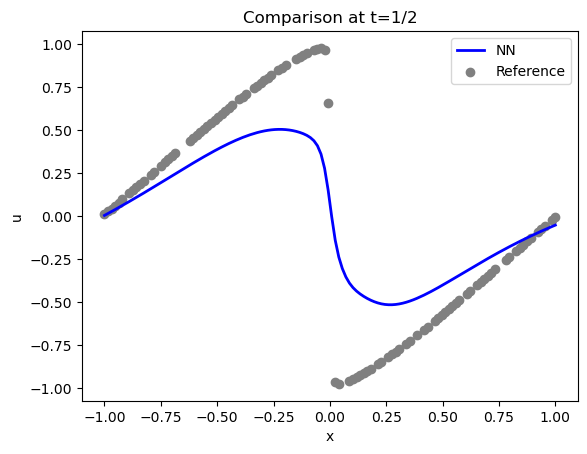
域两侧的情况还不错(满足了 Dirichlet 边界条件 ),但中心(位于 )的激波没有得到很好的表现。
让我们来看看 时的初始状态重建得如何。这是最有趣、也是最棘手的部分(其余部分基本上都是根据模型方程和边界条件,给出第一种状态)。
事实证明,初始状态的精确度其实并不高:PINN 的蓝色曲线与参考数据(灰色显示)的约束条件相去甚远...随着迭代次数的增加,求解结果会越来越好,但对于这种相当简单的情况来说,迭代次数之多令人吃惊。
# ground truth solution at t0
t0gt = np.asarray( [ [-math.sin(np.pi * x) * 1.] for x in np.linspace(-1,1,N)] )
velP0 = u[0,:,0,0]
fig = plt.figure().gca()
fig.plot(np.linspace(-1,1,len(velP0)), velP0, lw=2, color='blue', label="NN")
fig.plot(np.linspace(-1,1,len(t0gt)), t0gt, lw=2, color='gray', label="Reference")
plt.title("Comparison at t=0")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()
运行结果为:
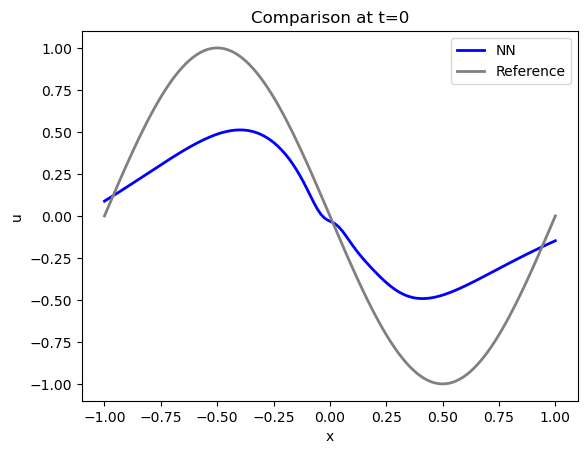
尤其是处的最大值/最小值相差甚远,而处的边界不符合要求:解不为零。
我们有用于该模拟的前向模拟器,因此我们可以使用网络的 解来评估时间评估的重建效果。这可以衡量通过 PINN 损失的软约束捕捉模型方程时间演化的程度。
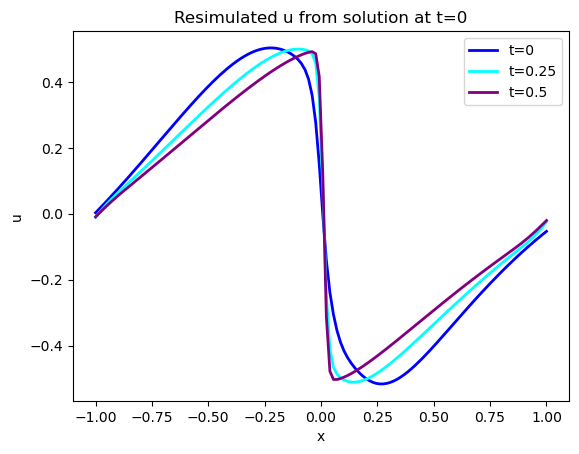
下图显示了蓝色的初始状态,以及在 和 时的两个演化状态。请注意,这些都是模拟版本,接下来我们将展示学习版本。
(注:下面的代码段还有一些可选代码,用于显示[STEPS//4]处的状态。默认情况下这些代码都已注释,如果你愿意,可以取消注释或添加额外的代码,以显示更多的时间演化过程)。
# re-simulate with phiflow from solution at t=0
DT = 1./32.
STEPS = 32-BC_TX # depends on where BCs were imposed
INITIAL = u[...,BC_TX:(BC_TX+1),0] # np.reshape(u0, [1,len(u0),1])
print(INITIAL.shape)
DOMAIN = Domain([N], boundaries=PERIODIC, box=box[-1:1])
state = [BurgersVelocity(DOMAIN, velocity=INITIAL, viscosity=0.01/np.pi)]
physics = Burgers()
for i in range(STEPS):
state.append( physics.step(state[-1],dt=DT) )
# we only need "velocity.data" from each phiflow state
vel_resim = [x.velocity.data for x in state]
fig = plt.figure().gca()
pltx = np.linspace(-1,1,len(vel_resim[0].flatten()))
fig.plot(pltx, vel_resim[ 0].flatten(), lw=2, color='blue', label="t=0")
#fig.plot(pltx, vel_resim[STEPS//4].flatten(), lw=2, color='green', label="t=0.125")
fig.plot(pltx, vel_resim[STEPS//2].flatten(), lw=2, color='cyan', label="t=0.25")
fig.plot(pltx, vel_resim[STEPS-1].flatten(), lw=2, color='purple',label="t=0.5")
#fig.plot(pltx, t0gt, lw=2, color='gray', label="t=0 Reference") # optionally show GT, compare to blue
plt.title("Resimulated u from solution at t=0")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()
注:如果报错
np.object was a deprecated...则需要修改:
- 文件
C:\ProgramData\anaconda3\Lib\site-packages\phi\backend\scipy_backend.py第64行- 文件
C:\ProgramData\anaconda3\Lib\site-packages\phi\struct\struct.py第306行- 文件
C:\ProgramData\anaconda3\Lib\site-packages\phi\struct\struct.py第315行修改
np.object为np.dtype('O')
下面是 u 在相同时间步长下的 PINN 输出:
velP = [u[0,:,x,0] for x in range(33)]
print(velP[0].shape)
fig = plt.figure().gca()
fig.plot(pltx, velP[BC_TX+ 0].flatten(), lw=2, color='blue', label="t=0")
#fig.plot(pltx, velP[BC_TX+STEPS//4].flatten(), lw=2, color='green', label="t=0.125")
fig.plot(pltx, velP[BC_TX+STEPS//2].flatten(), lw=2, color='cyan', label="t=0.25")
fig.plot(pltx, velP[BC_TX+STEPS-1].flatten(), lw=2, color='purple',label="t=0.5")
plt.title("NN Output")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()

根据目测标准判断,这两个版本的 看起来非常相似,但随着时间的推移,误差会逐渐增大,存在显著差异,这并不奇怪。尤其是在处激波附近解的陡峭化没有被很好地 "捕捉 "到。不过从这两幅图中很难看出来,让我们量化误差,显示实际差异:
error = np.sum( np.abs( np.asarray(vel_resim[0:16]).flatten() - np.asarray(velP[BC_TX:BC_TX+STEPS]).flatten() )) / (STEPS*N)
print("Mean absolute error for re-simulation across {} steps: {:7.5f}".format(STEPS,error))
fig = plt.figure().gca()
fig.plot(pltx, (vel_resim[0 ].flatten()-velP[BC_TX ].flatten()), lw=2, color='blue', label="t=5")
fig.plot(pltx, (vel_resim[STEPS//4].flatten()-velP[BC_TX+STEPS//4].flatten()), lw=2, color='green', label="t=0.625")
fig.plot(pltx, (vel_resim[STEPS//2].flatten()-velP[BC_TX+STEPS//2].flatten()), lw=2, color='cyan', label="t=0.75")
fig.plot(pltx, (vel_resim[STEPS-1 ].flatten()-velP[BC_TX+STEPS-1 ].flatten()), lw=2, color='purple',label="t=1")
plt.title("u Error")
plt.xlabel('x'); plt.ylabel('MAE'); plt.legend()
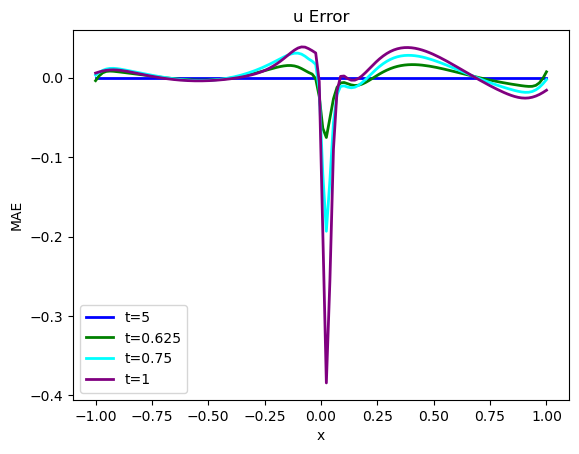
上述代码将计算出地面实况再模拟与 PINN 演化之间的平均绝对误差约为 ,这对于模拟的数值范围而言意义重大。为了与正向模拟和后续案例进行比较,这里还提供了所有随时间变化的步骤,并配有彩色地图。
# show re-simulated solution again as full image over time
sn = np.concatenate(vel_resim, axis=-1)
sn = np.reshape(sn, list(sn.shape)+[1] ) # print(sn.shape)
show_state(sn,"Re-simulated u")

接下来,我们将存储 时间间隔内的完整解,以便稍后将其与常规正向求解的完整解进行比较,并与微分物理解进行比较。因此,请继续关注完整的评估和比较。这将在Burgers Optimization with a Differentiable Physics Gradient中,在我们讨论完如何运行微分物理优化的细节之后进行。
vels = session.run(grid_u) # special for showing NN results, run through TF
vels = np.reshape( vels, [vels.shape[1],vels.shape[2]] )
# save for comparison with other methods
import os; os.makedirs("./temp",exist_ok=True)
np.savez_compressed("./temp/burgers-pinn-solution.npz",vels) ; print("Vels array shape: "+format(vels.shape))
结果为:
Vels array shape: (128, 33)
5.5 后续步骤
当然,这种设置只是 PINN 和物理软约束的一个起点。设置参数的选择是为了相对快速地运行。正如我们在接下来的章节中所展示的,通过将求解器和学习更紧密地结合在一起,这种逆求解的性能可以得到大幅提升。
不过,上述 PINN 设置的解也可以直接加以改进。例如,可以尝试:
- 调整训练参数,以进一步减少误差,同时不使解发散。
- 调整 NN 架构以进一步改进(但要跟踪权重计数)。
- 激活不同的优化器,并观察其行为变化(这通常需要调整学习率)。请注意,在这个相对简单的例子中,更复杂的优化器并不一定做得更好。
- 或者修改设置,使测试案例更有趣:例如,将边界条件移到模拟时间的较后一点,使重建的时间间隔更大。
目前的好消息是我们有了一种 DL 方法,可以通过最小化残差,以软约束的形式包含物理定律。不过,正如前面那个非常简单的例子所示,这只是一个概念上的起点。
积极的一面是,我们可以利用反向传播的 DL 框架来计算模型的导数。与此同时,这也使我们在这些导数的可靠性方面受到所学表示法的支配。而且,每个导数都需要通过整个网络进行反向传播。这可能会非常昂贵,尤其是对于高阶导数。
虽然设置相对简单,但通常很难控制。NN 可以灵活地自行完善求解,但同时,当它不能专注于求解的正确区域时,就需要一些技巧。
6.1 这算是“机器学习”吗?
说到这里,大家可能还会想到一个问题:我们真的可以称它为机器学习吗?当然,这样的命名问题是肤浅的--如果一种算法是有用的,那么它叫什么名字并不重要。不过,在这里,这个问题有助于强调机器学习或优化等领域的算法通常具有的一些重要特性。
不把上一个笔记本的优化称为机器学习(ML)的一个主要原因是,我们测试和限制解的位置就是我们感兴趣的最终位置。因此,训练集、验证集和测试集之间没有真正的区别。为已知和给定的样本集计算解更类似于经典优化,而之前的Burgers例子等逆问题就源于经典优化。
对于机器学习而言,我们通常会假设模型的最终性能将在不同的、可能未知的输入集上进行评估。测试数据通常应能捕捉到这种超出分布范围(OOD)的行为,这样我们就能对模型在 "真实世界 "中的泛化程度做出估计,而这些 "真实世界 "是我们在应用中部署模型时会遇到的。
与此相反,在本文所述的 PINN 训练中,我们在已知和给定的时空区域内重建一个单一的解。因此,来自该区域的任何样本都遵循相同的分布,因此并不能真正代表测试或 OOD 样本。由于 NN 直接对解法进行编码,因此它几乎不可能产生不同的解法,也不可能在训练范围之外表现出色。如果我们对不同的解感兴趣,就必须从头开始训练 NN。

6.2 总结
因此,通过物理软约束,我们可以利用 NN 工具对 PDE 的解进行编码。这种变式 2 的一个固有缺点是只能得到单一的解,而且不能很好地与传统的数值技术相结合。例如,学习到的表征不适合用共轭梯度法等经典迭代求解器来完善。
这意味着过去几十年中开发的许多强大技术无法在此背景下使用。让这些数值方法重新发挥作用,将是接下来几节的核心目标之一。
✅ 优点:
- 使用物理模型。
- 可以通过反向传播方便地计算导数。
❌ 缺点:
- 相当缓慢......
- 物理约束仅作为软约束施加。
- 在很大程度上与经典数值方法不兼容。
- 导数的准确性依赖于学习到的表示。
为了解决这些问题,我们接下来将研究如何利用现有的数值方法,通过使用可微分求解器来改进 DL 流程。
作为深度学习方法与物理模拟更紧密、更通用结合的下一步,我们将把可微分数值模拟纳入到学习过程中。在下文中,我们将 "物理系统的可微分数值模拟 "简称为 "可微分物理"(DP)。
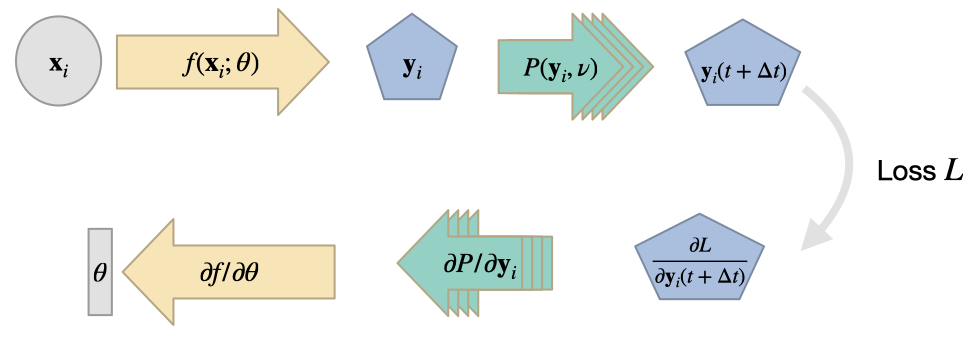
这些方法的核心目标是利用现有的数值求解器,并为其配备根据输入计算梯度的功能。一旦模拟的所有算子都实现了这一功能,我们就可以利用 DL 框架的反向传播自动微分功能,实现让梯度信息从模拟器流入 NN,反之亦然。这样做有很多好处,如改进学习反馈和泛化,我们将在下文概述。
与集成物理约束的损失函数方法相比, 它还能够处理更为复杂的解空间, 而不仅仅是一个反问题。例如, 在前一章中我们使用深度学习来解决单一的反问题, 而利用可微物理学, 我们可以训练神经网络以非常高效地解决更大类别的反问题。
7.1 可微算子
通过DP方法,我们在现有的数值求解器基础上进行建模。也就是说,这种方法在很大程度上依赖于计算方法领域为我们世界中各种物理效应开发的算法。首先,我们需要一个连续的数学模型来描述我们想要模拟的物理效应,如果没有这个模型,我们就会遇到麻烦。但幸运的是,我们可以利用现有的模型方程集合和离散化连续模型的已建立方法。
假设我们有一个关于感兴趣的物理量 的连续表达式,其中 是模型参数(例如扩散系数、粘度或电导率)。 的分量将用编号的下标表示,即 。
通常,我们对这样一个系统的时间演化感兴趣。离散化得到一个公式 ,我们重新排列以计算时间步长 后的未来状态。在 时刻,通过一系列操作 来计算,使得 ,其中 表示函数分解,即 。
注:为了将这个求解器整合到深度学习过程中,我们需要确保每个算子相对于其输入提供梯度,即在上述示例中为。
请注意,我们通常不需要的所有参数的导数,例如,我们在下文中省略了,假设这是一个给定的模型参数,NN不应该与之交互。当然,它可以在我们感兴趣的解流形中变化,但 不会成为 NN 表示的输出。如果是这种情况,我们就可以在求解器中省略提供 。然而,下面的学习过程自然会将 作为一个自由度。
请注意,通常我们不需要计算的所有参数的导数,例如,在接下来的内容中我们省略了,假设这是一个给定的模型参数,神经网络不应该与之交互。当然,它可以在我们感兴趣的解空间内变化,但不会是神经网络表示的输出。如果是这种情况,我们可以在求解器中省略提供。然而,下面的学习过程自然地可以包含作为一个自由度。
7.2 雅可比矩阵
由于 通常是一个向量值函数,所以 表示雅各布矩阵 ,而不是单一值:
\begin{aligned} \frac{ \partial \mathcal P_i }{ \partial \mathbf{u} } = \begin{bmatrix} \partial \mathcal P_{i,1} / \partial u_{1} & \ \cdots \ & \partial \mathcal P_{i,1} / \partial u_{d} \ \vdots & \ & \ \ \partial \mathcal P_{i,d} / \partial u_{1} & \ \cdots \ & \partial \mathcal P_{i,d} / \partial u_{d} \end{bmatrix} \end{aligned}
如上所述, 表示向量 中的分量数。由于 将 的一个值映射到另一个值,因此在这里雅可比矩阵是方阵。当然,这并不一定是一般模型方程的情况,但对于可微分模拟来说,非方阵的雅可比矩阵并不会造成任何问题。
在实践中,我们依赖现代深度学习框架提供的_反向模式_微分,关注计算雅可比矩阵的转置与一个向量 的矩阵向量积,即表达式: 。如果我们需要在训练过程中构建和存储遇到的所有完整雅可比矩阵, 将导致巨大的内存开销并不必要地减慢训练速度。相反, 对于反向传播, 我们可以提供更快的运算来计算与雅可比转置的乘积, 因为链式规则的末端总是一个标量的损失函数。
考虑到上面的表述,我们需要通过链式规则来求解 在某个当前状态 下的函数组成链的导数。例如,对于其中的两个:
这只是“经典”链式法则 的向量版本,并直接扩展到更多级联函数的情况 ()。
这里,和的导数仍然是雅可比矩阵,但需要注意的是,在链的“末端”,我们有标量损失(参见Overview),最右边的雅可比矩阵将始终是一个具有1列的矩阵,即一个向量。在反向模式下,我们从该向量开始,逐个计算与左侧雅可比矩阵的乘积。
前向和反向传播模式微分的详细内容, 请参阅诸如 Baydin等人的综述之类的外部材料。
7.3 基于 DP 算子的学习
因此,一旦我们模拟器的算子支持雅各布向量乘积的计算,我们就可以将它们集成到 DL 管道中,就像集成普通全连接层或 ReLU 激活一样。
此时,会出现一个非常合理的问题:“大多数物理求解器可以分解为一系列向量和矩阵操作。所有最先进的深度学习框架都支持这些操作,那么我们为什么不直接使用这些操作来实现我们的物理求解器呢?”
确实在理论上这是可能的。但问题是,TensorFlow和PyTorch中的每个向量和矩阵操作都是单独计算的,并且内部需要存储当前的前向计算状态以进行反向传播(上述的“”)。然而对于一个典型的模拟来讲,我们并不太关注求解器产生的每个中间结果。我们通常更关注诸如从 到 等重要更新步骤。
因此,在实践中,将求解过程分解为一系列有意义但单一的操作符是一个非常好的主意。这不仅通过防止计算不必要的中间结果节省了大量的工作,还允许我们选择计算这些操作符的更新(和导数)的最佳可能的数字方法。例如,由于这个过程与伴随法优化非常相似,我们可以重用在这个领域开发的许多技术,或者利用已有的数字方法。例如,我们可以利用多网格求解器的运行时来进行矩阵求逆。
这种方法的不利之处是,它需要对手头的问题和数值方法有一定的了解。此外,给定的求解器可能无法直接提供梯度计算。因此,如果我们想将深度学习应用于我们没有充分理解的模型方程,通过可微物理(Differentiable Physics,DP)方法进行学习可能不是一个好主意。然而,如果我们真的不理解我们的模型,我们最好还是回去再深入研究一下...
在实践中,我们应该对导数运算符采取贪婪的策略,并且只提供与学习任务相关的那些。例如,如果我们的网络在上述例子中从未产生参数,并且在我们的损失公式中也没有出现导数,那么我们在反向传播步骤中就永远不会遇到导数。
下图总结了基于 DP 的学习方法,并说明了一次 PDE 求解中通常要处理的运算序列。由于许多运算在实践中是非线性的,这通常会使神经网络面临具有挑战性的学习任务:

7.4 一个实际例子
举个简单的例子,我们考虑将被动标量密度在速度场中的对流作为物理模型:
我们不直接将其作为残差方程使用 (如4 物理损失中的 v2), 而是用我们喜欢的网格和离散化方案对其进行离散化, 以获得一个随时间更新系统状态的表达式。这是一个标准的_前向_求解过程。为简化起见, 我们这里假设 仅仅是空间中的函数, 即随时间保持不变。我们稍后会讨论 的时间演化。
我们将这个重新表达式表示为 。它将 的状态映射到演化后的新状态,即:
作为逆问题和学习任务的简单示例,让我们考虑找到速度场的问题。这个速度应该将给定的初始标量密度状态在时间转变为由演化到稍后“结束”时间的状态,具有某种形状或配置。通俗地说,我们希望找到一个流场,通过PDE模型将变形为目标状态。表达这一目标的最简单方法是通过两种状态之间的L2损失。因此,我们想要最小化损失函数。
作为逆问题和学习任务的一个简单例子,我们来考虑寻找速度场 的问题。这个速度应该能将时间 时的给定初始标量密度状态 转变为一个状态,这个状态通过 演化到之后的 "结束 "时间 ,并具有一定的形状或配置 。非正式地讲,我们希望找到一种流,通过 PDE 模型将 变形为目标状态。表达这一目标的最简单方法是两个状态之间的 损失。因此,我们希望最小化损失函数 。
请注意,这里描述的这个反问题是一个纯粹的优化任务:不涉及 NN,我们的目标是获得 。我们并不希望将这一速度应用到其他未见过的_测试数据_上,这在实际学习任务中是很常见的。
我们的标记密度 的最终状态完全由通过 从 开始的演化决定,这就产生了下面的最小化问题:
现在,我们想通过梯度下降(GD)找到这个目标的最小值,梯度由本章前面介绍的可微分物理方法决定。一旦使用梯度下降法,我们就可以比较容易地切换到更好的优化器,或将 NN 引入其中,因此它始终是一个很好的起点。为了方便阅读,我们在下文中将省略雅克比矩阵的转置。不幸的是, 雅克比因子是这样定义的,但我们实际上并不需要未转置的雅克比因子。请记住,实际上我们处理的是转置的雅克比矩阵 ,它被 "缩写 "了。
由于离散化的速度场 包含了所有的自由度,我们所需要做的就是通过 来更新速度,它被分解为 。 分量部分通常很简单:我们会得到
如果将 表示为一个向量,例如网格的每个单元都有一个条目,那么 同样也将是一个大小相当的列向量。这是因为 始终是一个标量损失函数,因此雅克比矩阵在 维度上的维数为 1。直观地说,这个向量将简单地包含结束时间的 与目标密度 之间的差值。
本身的演化是由我们的离散物理模型 给出的,我们可以互换使用 和 。因此,更有趣的部分是雅可比矩阵 来计算完整的 。幸运的是,我们不需要 作为一个完整的矩阵,而只需要它与的乘积。
那么,的实际雅可比矩阵是什么呢?为了计算它,我们首先需要完善偏微分方程模型 ,这样可以得到一个可以求导的表达式。在下一章节中,我们将选择一个特定的对流格式和离散化方法,以便我们可以更具体地讨论。
7.4.1 引入一个具体的对流格式
下面我们将在 1 D 笛卡尔网格上使用一个简单的一阶迎风格式,其中单元 具有标量密度 和速度 。为简洁起见, 我们省略时间 处量的标注 ,即下面 简写为 。从上面可以看到, 我们使用_物理模型_更新标量密度 ,其中:

因此, 对于负的 ,我们使用 沿速度相反的方向查看, 即运动学意义上的_后向_。在这种情况下 将为零。对于正的 则反之, 我们将得到一个零值的 ,并通过 得到一个后向差分模板。为了选择前一种情况, 对于负的 我们得到:
因此 给出了 。直观地看,速度的变化取决于密度的空间导数。由于采用了一阶迎风格式,我们只考虑了两个相邻点(高阶方法会依赖的更多项)。
实际上,这一步等同于计算转置矩阵乘法。如果我们把上面的计算改写成 ,那么 。然而,在许多实际情况下,这种乘法的无矩阵实现可能比实际构造 更可取。
对于对流格式,我们可以考虑的另一个导数是与之前密度状态相关的导数,即 ,简写为 。对于单元 ,从上面的得出。然而,为了得到完整的梯度,我们需要加上来自 和 单元的潜在贡献,这取决于它们速度的符号。这种导数将在下一节中发挥作用。
7.4.2 时间演化
到目前为止,我们只处理了从时间 到 的一个 更新步,但我们当然可以有任意数量的这样的步骤。毕竟,我们在上文提出的目标是将初始标记状态 提前到时间 时的目标状态,这可能涵盖很长的时间间隔。
在上面的表达式中,每个都依次取决于时的速度和密度状态,即。因此,我们必须追溯损失 的影响,一直追溯到 如何影响初始标记状态。这可能需要通过 对对流格式进行大量评估。
这初听起来很有挑战性:例如,我们可以尝试将时间为的方程(1)插入时间为的方程,然后递归地重复这一过程,直到我们得到一个将与目标相关联的单一表达式。然而,由于雅可比矩阵的线性性质,我们将每个对流步骤,即我们的 PDE 的每次调用视为单独的模块化操作。每一次调用都遵循上一节描述的程序。
给定上述机制, 反向追踪非常简单: 对于 中的每个对流步骤, 我们计算雅可比矩阵与来自损失 或前一个对流步骤的导数的_输入_向量的乘积。我们重复这个过程直到追踪链条从具有 的损失一直回溯到 。从理论上讲, 速度 可以像 一样是时间的函数, 在这种情况下, 我们在每个时间步 都会得到一个梯度 。然而, 为了简化下面的内容, 我们假设我们有一个随时间不变的场, 即我们对每个通过 的对流都重用相同的速度 。现在, 每个时间步骤都会为我们提供一个对 的贡献,我们对所有步骤进行累积。
这里最后一项包含了从时间 到目标时间的完整标量密度回溯。乍看之下, 和式中的各项很令人困惑, 但仔细看, 左边每一行都只是添加了一个额外的时间步的雅可比矩阵。这遵循上面两个算子情况下的链式法则。因此各项包含许多相似的雅可比矩阵, 在实践中可以通过反向遍历 PDE 前向求解生成的计算步骤序列来有效计算。(如上所述, 这里我们省略了雅可比矩阵的转置。)
这种结构也清楚地表明,这一过程与 NN 的常规训练过程非常相似:通过嵌套函数调用对这些雅可比向量积进行评估,这正是深度学习框架训练 NN 的过程(我们只是用权重 代替了速度场)。因此,我们在实践中需要做的就是为 提供一个雅可比向量积的自定义函数。
7.5 隐式梯度计算
作为一个稍微复杂一点的例子,让我们考虑一下泊松方程 ,其中 是感兴趣的量,而 是给定的值。这是一个非常基本的椭圆多项式方程,对从静电到引力场等各种物理问题都很重要。它也出现在流体中,其中 是流体中的标量压力场,而右边的 则由流体速度 的散度给出。
对于流体,我们通常有 ,其中 。这里, 表示新的、无散度的速度场。这一步通常对执行硬约束 至关重要,也被称为 Chorin Projection,或 Helmholtz decomposition。它是向量微积分基本定理的直接结果。
如果我们现在在求解器中引入一个可以修改 的 NN,我们不可避免地需要通过泊松求解进行反向传播。也就是说,我们需要的梯度,在这个符号中,梯度的形式是.
结合起来,我们的目标是计算 。外部梯度(来自 )和内部散度()都是线性算子,它们的梯度很容易计算。主要的困难在于如何从泊松方程中获得逆矩阵 (我们在此将其简化一些,但它通常与时间相关,而且是非线性的)。
在实践中,对于的的矩阵向量乘积并不是通过矩阵运算显式计算得到,而是用一个(可能是无矩阵的)迭代求解器来近似计算。例如,共轭梯度(CG)方法在这里非常受欢迎。因此,我们可以理论上将这个迭代求解器视为一个函数,其中。值得注意的是,矩阵求逆是一个非线性的过程,尽管矩阵本身是线性的。由于像CG这样的求解器也是基于矩阵和向量操作的,我们可以将分解为所有求解器迭代过程中一系列简单操作的序列,如,并通过每个操作进行反向传播。这当然是可行的,但不是一个好主意:它可能会引入数值问题,并且会非常慢。如上所述,DL框架默认存储像这个例子中的每一个可微算子(如本例中的)内部状态,因此我们需要组织和保留大量的中间状态在内存中。尽管这些状态对于我们原始的PDE来说完全没有意义,它们只是CG求解器的中间状态。
如果我们退后一步来看,它的梯度就是。在这种情况下,是一个对称矩阵,因此。这是我们在上面的原始方程中遇到的相同逆矩阵,因此我们重复使用未修改的迭代求解器来计算梯度。我们不需要拆开它并通过存储中间状态来减慢速度。然而,迭代求解器计算的矩阵向量乘积。那么在反向传播过程中是什么?在优化设置中,我们总是在正向传播链的末尾有损失函数。反向传播步骤将为输出给出一个梯度,假设这里是,需要传播到正向传播过程的较早操作。因此,我们只需在反向传播过程中调用我们的迭代求解器来计算。假设我们已经选择了一个良好的求解器用于正向传播,那么在反向传播中我们将得到完全相同的性能和精度。
如果您对代码示例感兴趣,phiflow的differentiate-pressure example正是使用这个过程进行通过压力投影步骤进行优化的:一个在右侧受限的流场,通过左侧的内容进行优化,以便在压力投影步骤后与右侧的目标匹配。
这里的主要启示是:在前向计算中,重要的是_不要盲目地进行反向传播_,而是要考虑在前向传递的解析方程中,为哪几步计算梯度。在上述情况下,我们通常可以找到梯度的改进解析表达式,然后对其进行数值逼近。
隐式函数定理和时间 IFT:上述过程本质上产生隐式导数。我们没有显式推导所有前向步骤,而是依靠隐函数定理来计算导数。 Time:我们实际上可以将迭代求解器的步骤视为虚拟的“时间”,并通过这些步骤进行反向传播。与其他Dp方法一样,这使得神经网络能够与迭代求解器交互。一个例子是从 [UBH+20] 中学习 CG 求解器的初始猜测。详细信息和代码可以在这里找到。
7.6 到目前为止可微物理模拟的总结
总结一下, 使用可微物理模拟为我们提供了一种工具, 可以将选择的离散化的物理方程引入深度学习中。与前一章的残差约束相比, 这使得神经网络可以无缝地与物理求解器进行交互。
以前我们会在神经网络训练结束后完全放弃物理模型和求解器: 在5 PINN优化Burgers方程 的例子中,神经网络直接给出解,绕过任何求解器或模型方程。DP 方法与5 PINN优化Burgers方程 中的基于物理的神经网络 (v 2)有本质区别,它与受控离散化 (v 1)更加接近。后者实际上是 DP 训练的一个子集或部分应用。
然而, 与这两种残差方法相反, DP 使得神经网络可以与数值求解器一起训练,因此我们可以在之后的推理时利用物理模型 (由求解器表示)。这使我们能够解决单一的反问题, 并使神经网络对新的输入具有非常强的泛化能力。让我们在 DP 的背景下重新审视5 PINN优化Burgers方程中的示例问题。
- 我们不再仅仅预测残差,而是训练一个神经网络来预测速度场。
- 该速度场不再直接用于计算损失,而是作为输入馈送到物理求解器中。
- 求解器使用预测的速度场进一步演化标量密度场。
- 最终的标量密度场与目标进行比较,计算损失。
- 梯度通过求解器反向传播, 更新神经网络的参数。
这样, 训练好的网络就学会了预测一个速度场, 这场速度场能够通过物理方程的演化得到目标状态。在部署阶段, 我们可以继续使用物理求解器, 只是用训练好的网络来替代速度场的生成。这种方法增强了对物理约束的遵循性, 并提高了泛化能力。
为了说明在可微分物理(DP)环境中计算梯度的过程,我们以5 PINN优化Burgers方程中 PINN 示例中使用的相同逆问题(重建任务)为目标。选择 DP 方法会产生一些直接影响:我们从离散化的 PDE 开始,系统的演化现在完全由由此产生的数值求解器决定。因此,真正的未知数只有初始状态。我们仍然需要多次重新计算初始状态和目标状态之间的所有状态,只是现在我们不需要 NN 来完成这一步骤。取而代之的是模型方程的离散化。
另外, 由于我们为 DP 方法选择了一个初始离散化, 未知的初始状态由涉及的物理场的采样点组成, 我们可以简单地将这些未知量表示为浮点变量。因此, 即使对于初始状态, 我们也不需要建立神经网络。因此, 使用 DP 来解决的 Burgers 重建问题简化为没有任何神经网络的基于梯度的优化。尽管如此, 这仍然是一个非常好的起点来说明这个过程。
首先,我们将设置离散模拟。这里我们使用 phiflow,如Burgers forward simulations概述部分所示。
8.1 初始化
如果我们不使用 numpy 后端,phiflow 可以直接为我们提供可微分的操作序列。这里重要的一步是加入 phi.tf.flow 代替 phi.flow (对于 pytorch,可以使用 phi.torch.flow)。
因此,第一步,让我们设置一些常量,并将velocity场初始化为零,并将我们的约束条件设置为 (步骤 16),现在作为 phiflow 中的CenteredGrid。两者都使用周期性边界条件(通过 extrapolation.PERIODIC)和 的空间离散化。
!pip install --upgrade --quiet phiflow==2.2
from phi.tf.flow import *
N = 128
DX = 2/N
STEPS = 32
DT = 1/STEPS
NU = 0.01/(N*np.pi)
# allocate velocity grid
velocity = CenteredGrid(0, extrapolation.PERIODIC, x=N, bounds=Box(x=(-1,1)))
# and a grid with the reference solution
REFERENCE_DATA = math.tensor([0.008612174447657694, 0.02584669669548606, 0.043136357266407785, 0.060491074685516746, 0.07793926183951633, 0.0954779141740818, 0.11311894389663882, 0.1308497114054023, 0.14867023658641343, 0.1665634396808965, 0.18452263429574314, 0.20253084411376132, 0.22057828799835133, 0.23865132431365316, 0.25673879161339097, 0.27483167307082423, 0.2929182325574904, 0.3109944766354339, 0.3290477753208284, 0.34707880794585116, 0.36507311960102307, 0.38303584302507954, 0.40094962955534186, 0.4188235294008765, 0.4366357052408043, 0.45439856841363885, 0.4720845505219581, 0.4897081943759776, 0.5072391070000235, 0.5247011051514834, 0.542067187709797, 0.5593576751669057, 0.5765465453632126, 0.5936507311857876, 0.6106452944663003, 0.6275435911624945, 0.6443221318186165, 0.6609900633731869, 0.67752574922899, 0.6939334022562877, 0.7101938106059631, 0.7263049537163667, 0.7422506131457406, 0.7580207366534812, 0.7736033721649875, 0.7889776974379873, 0.8041371279965555, 0.8190465276590387, 0.8337064887158392, 0.8480617965162781, 0.8621229412131242, 0.8758057344502199, 0.8891341984763013, 0.9019806505391214, 0.9143881632159129, 0.9261597966464793, 0.9373647624856912, 0.9476871303793314, 0.9572273019669029, 0.9654367940878237, 0.9724097482283165, 0.9767381835635638, 0.9669484658390122, 0.659083299684951, -0.659083180712816, -0.9669485121167052, -0.9767382069792288, -0.9724097635533602, -0.9654367970450167, -0.9572273263645859, -0.9476871280825523, -0.9373647681120841, -0.9261598056102645, -0.9143881718456056, -0.9019807055316369, -0.8891341634240081, -0.8758057205293912, -0.8621229450911845, -0.8480618138204272, -0.833706571569058, -0.8190466131476127, -0.8041372124868691, -0.7889777195422356, -0.7736033858767385, -0.758020740007683, -0.7422507481169578, -0.7263049162371344, -0.7101938950789042, -0.6939334061553678, -0.677525822052029, -0.6609901538934517, -0.6443222327338847, -0.6275436932970322, -0.6106454472814152, -0.5936507836778451, -0.5765466491708988, -0.5593578078967361, -0.5420672759411125, -0.5247011730988912, -0.5072391580614087, -0.4897082914472909, -0.47208460952428394, -0.4543985995006753, -0.4366355580500639, -0.41882350871539187, -0.40094955631843376, -0.38303594105786365, -0.36507302109186685, -0.3470786936847069, -0.3290476440540586, -0.31099441589505206, -0.2929180880304103, -0.27483158663081614, -0.2567388003912687, -0.2386513127155433, -0.22057831776499126, -0.20253089403524566, -0.18452269630486776, -0.1665634500729787, -0.14867027528284874, -0.13084990929476334, -0.1131191325854089, -0.09547794429803691, -0.07793928430794522, -0.06049114408297565, -0.0431364527809777, -0.025846763281087953, -0.00861212501518312] , math.spatial('x'))
SOLUTION_T16 = CenteredGrid( REFERENCE_DATA, extrapolation.PERIODIC, x=N, bounds=Box(x=(-1,1)))
下面我们将验证我们模拟的物理场现在是否得到了 TensorFlow 的支持。
type(velocity.values.native())
tensorflow.python.framework.ops.EagerTensor
8.2 梯度
phiflow的math.gradient操作生成一个用于标量损失的梯度函数,我们在下面使用它为选择的32个时间步长的整个模拟计算梯度。
为了在Burgers方程中使用它,我们需要计算一个适当的损失函数:我们希望在时的解与参考数据匹配。因此,我们简单地计算步骤16和约束数组之间的差异作为loss。然后,我们计算初始速度状态velocity相对于该损失的梯度函数。Phiflow的math.gradient生成一个函数,该函数返回每个参数的梯度,由于我们这里只有一个速度参数,所以grad[0]表示初始速度的梯度。
def loss_function(velocity):
velocities = [velocity]
for time_step in range(STEPS):
v1 = diffuse.explicit(1.0*velocities[-1], NU, DT, substeps=1)
v2 = advect.semi_lagrangian(v1, v1, DT)
velocities.append(v2)
loss = field.l2_loss(velocities[16] - SOLUTION_T16)*2./N # MSE
return loss, velocities
gradient_function = math.gradient(loss_function)
(loss,velocities), grad = gradient_function(velocity)
print('Loss: %f' % (loss))
Loss: 0.382915
因为我们只约束了第16个时间步长,所以在这个设置中我们实际上可以省略第17到31步。它们没有任何自由度,也没有受到任何约束。然而,为了与之前的情况进行公平比较,我们将它们包括在内。
请注意,我们在这里进行了很多计算:首先是32步模拟,然后是从损失开始的另外16步的反向传播。它们由梯度记录下来,并用于将损失反向传播到模拟的初始状态。
毫不奇怪,因为我们从零开始,第16个模拟步的初始误差也很大,约为0.38。
那么在这里我们得到了什么样的梯度呢?它与速度具有相同的维度,我们可以很容易地将其可视化:从零状态的velocity开始(显示为蓝色),第一个梯度显示为下方的绿线。如果将其与解进行比较, 可以看到它与预期的方向相反。解的大小要大得多,因此我们在这里省略了它(请参见下一个图表)。
import pylab as plt
fig = plt.figure().gca()
pltx = np.linspace(-1,1,N)
# first gradient
fig.plot(pltx, grad[0].values.numpy('x') , lw=2, color='green', label="Gradient")
fig.plot(pltx, velocity.values.numpy('x'), lw=2, color='mediumblue', label="u at t=0")
plt.xlabel('x'); plt.ylabel('u'); plt.legend();
# some (optional) other fields to plot:
# fig.plot(pltx, (velocities[16]).values.numpy('x') , lw=2, color='cyan', label="u at t=0.5")
# fig.plot(pltx, (SOLUTION_T16).values.numpy('x') , lw=2, color='red', label="solution at t=0.5")
# fig.plot(pltx, (velocities[16] - SOLUTION_T16).values.numpy('x') , lw=2, color='blue', label="difference at t=0.5")
运行结果为:
这为每个速度变量提供了一个“搜索方向”。基于线性近似,梯度告诉我们如何改变每个速度变量以增加损失函数(梯度始终指向“上方”)。因此,我们可以利用梯度进行优化,找到一个最小化损失的初始状态的速度velocity。
8.3 优化
我们现在使用梯度进行梯度下降优化。下面,我们使用学习率LR=5,并重新评估更新状态的损失以追踪收敛性。
在下面的代码块中,我们还将梯度保存在一个名为grads的列表中,以便稍后进行可视化。对于常规优化,当执行速度更新后,我们当然可以丢弃梯度。
LR = 5.
grads=[]
for optim_step in range(5):
(loss,velocities), grad = gradient_function(velocity)
print('Optimization step %d, loss: %f' % (optim_step,loss))
grads.append( grad[0] )
velocity = velocity - LR * grads[-1]
执行结果为:
Optimization step 0, loss: 0.382915
Optimization step 1, loss: 0.326882
Optimization step 2, loss: 0.281032
Optimization step 3, loss: 0.242804
Optimization step 4, loss: 0.210666
现在我们将仔细检查模拟的第16个状态是否与目标相匹配,这才是损失函数的衡量标准。下一个图表显示了约束条件(即我们希望获得的解)以绿色表示,并且在初始状态 velocity(通过梯度更新了五次)经过求解器进行了16次更新后的重构状态用蓝色表示。
fig = plt.figure().gca()
# target constraint at t=0.5
fig.plot(pltx, SOLUTION_T16.values.numpy('x'), lw=2, color='forestgreen', label="Reference")
# optimized state of our simulation after 16 steps
fig.plot(pltx, velocities[16].values.numpy('x'), lw=2, color='mediumblue', label="Simulated velocity")
plt.xlabel('x'); plt.ylabel('u'); plt.legend(); plt.title("After 5 Optimization Steps at t=0.5");
执行结果如下:
这似乎是朝着正确的方向发展!虽然还不完美,但我们目前只计算了5个梯度下降更新步骤。左侧激波上具有正速度的两个峰和右侧的负峰开始显现出来。
这是一个很好的指示,表明通过我们模拟的16个步骤反向传播的梯度表现正常,并且它正在推动解决方案朝着正确的方向发展。上面的图表只是暗示了这个设置有多么强大:我们从每个模拟步骤(以及其中的每个操作)获得的梯度可以轻松地链接成更复杂的序列。在上面的示例中,我们通过模拟的所有16个步骤进行了反向传播,通过对代码进行微小的修改,我们可以轻松地扩大这种优化的“前瞻”。
8.4 更多优化步骤
在进行更复杂的物理模拟或涉及神经网络之前,让我们先完成手头的优化任务,并运行更多步骤以获得更好的解。
import time
start = time.time()
for optim_step in range(5,50):
(loss,velocities), grad = gradient_function(velocity)
velocity = velocity - LR * grad[0]
if optim_step%5==0:
print('Optimization step %d, loss: %f' % (optim_step,loss))
end = time.time()
print("Runtime {:.2f}s".format(end-start))
运行结果:
Optimization step 5, loss: 0.183476
Optimization step 10, loss: 0.096224
Optimization step 15, loss: 0.054792
Optimization step 20, loss: 0.032819
Optimization step 25, loss: 0.020334
Optimization step 30, loss: 0.012852
Optimization step 35, loss: 0.008185
Optimization step 40, loss: 0.005186
Optimization step 45, loss: 0.003263
Runtime 130.33s
回想一下 Burgers Optimization with a Differentiable Physics Gradient中的 PINN 版本, 与可比运行时间下, 误差降低了大约两个数量级。这种行为源于 DP 为具有所有离散点和时间步骤的整个解提供梯度, 而不是局部更新。
让我们再次绘制我们在 处的解 (蓝色)与约束条件 (绿色)的匹配情况:
fig = plt.figure().gca()
fig.plot(pltx, SOLUTION_T16.values.numpy('x'), lw=2, color='forestgreen', label="Reference")
fig.plot(pltx, velocities[16].values.numpy('x'), lw=2, color='mediumblue', label="Simulated velocity")
plt.xlabel('x'); plt.ylabel('u'); plt.legend(); plt.title("After 50 Optimization Steps at t=0.5");
运行结果:
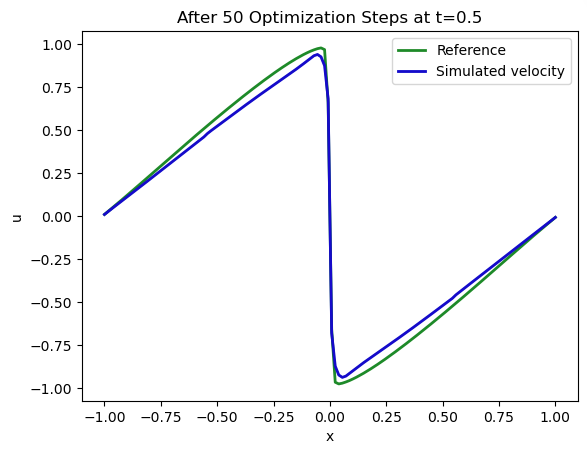
不错。但是通过 16 步模拟反向传播恢复的初始状态如何呢? 这是我们正在改变的, 而且因为它只通过后期的观测结果受到间接约束, 所以与期望的解或所需的解偏差的空间更大。
这在下一幅图中显示:
fig = plt.figure().gca()
pltx = np.linspace(-1,1,N)
# ground truth state at time=0 , move down
INITIAL_GT = np.asarray( [-np.sin(np.pi * x) for x in np.linspace(-1+DX/2,1-DX/2,N)] ) # 1D numpy array
fig.plot(pltx, INITIAL_GT.flatten() , lw=2, color='forestgreen', label="Ground truth initial state") # ground truth initial state of sim
fig.plot(pltx, velocity.values.numpy('x'), lw=2, color='mediumblue', label="Optimized initial state") # manual
plt.xlabel('x'); plt.ylabel('u'); plt.legend(); plt.title("Initial State After 50 Optimization Steps");
结果如下所示。
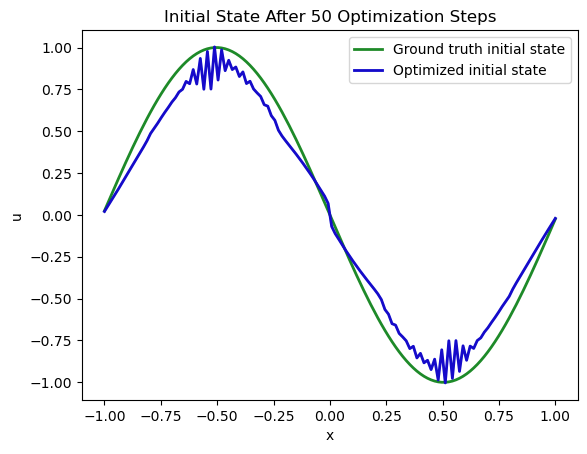
自然而然,这是一个更困难的任务:优化过程接收到了在时刻状态应该是什么的直接反馈,但由于非线性模型方程的存在,通常会有大量满足约束条件的解,这些解要么完全满足约束条件,要么在数值上非常接近。因此,我们的最小化器不一定能找到我们起始状态的确切解(在默认设置下,我们可以观察到扩散算子引起的一些数值振荡)。然而,在这个Burgers场景中,解仍然非常接近。
在衡量重建的整体误差之前,让我们可视化系统随时间的完整演化,因为这也会产生一个numpy数组形式的解,我们可以与其他版本进行比较。
import pylab
def show_state(a):
a=np.expand_dims(a, axis=2)
for i in range(4):
a = np.concatenate( [a,a] , axis=2)
a = np.reshape( a, [a.shape[0],a.shape[1]*a.shape[2]] )
fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
im = axes.imshow(a, origin='upper', cmap='inferno')
pylab.colorbar(im)
# get numpy versions of all states
vels = [ x.values.numpy('x,vector') for x in velocities]
# concatenate along vector/features dimension
vels = np.concatenate(vels, axis=-1)
# save for comparison with other methods
import os; os.makedirs("./temp",exist_ok=True)
np.savez_compressed("./temp/burgers-diffphys-solution.npz", np.reshape(vels,[N,STEPS+1])) # remove batch & channel dimension
show_state(vels)
结果如下:
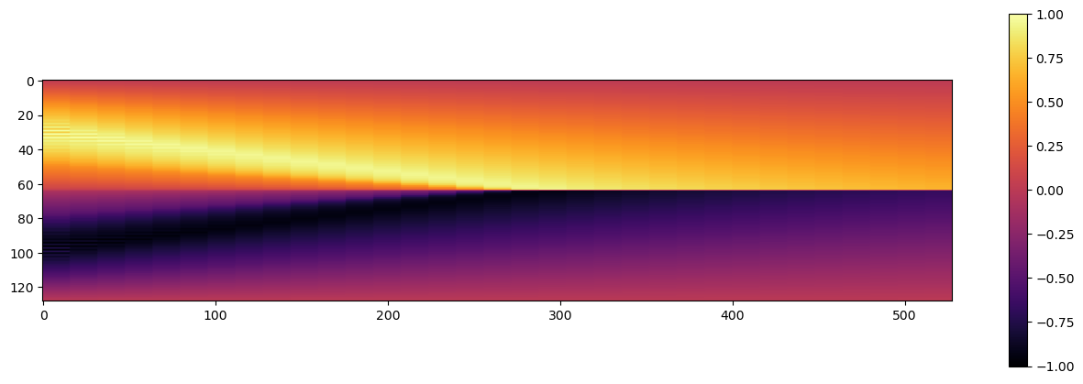
8.5 基于物理的 vs. 可微物理重建
现在我们有两个版本,一个是带有PINN的版本,另一个是DP版本,所以让我们更详细地比较这两个重建结果。(注意:以下单元格预期Burgers-forward和PINN笔记本在之前的相同环境中执行,以便./temp目录中的.npz文件可用。)
让我们首先并排查看这些解。下面的代码生成一个包含3个版本的图像,从上到下依次是:由常规正向模拟给出的真值(GT)解,中间是PINN重建,底部是可微分物理版本。
# note, this requires previous runs of the forward-sim & PINN notebooks in the same environment
sol_gt=npfile=np.load("./temp/burgers-groundtruth-solution.npz")["arr_0"]
sol_pi=npfile=np.load("./temp/burgers-pinn-solution.npz")["arr_0"]
sol_dp=npfile=np.load("./temp/burgers-diffphys-solution.npz")["arr_0"]
divider = np.ones([10,33])*-1. # we'll sneak in a block of -1s to show a black divider in the image
sbs = np.concatenate( [sol_gt, divider, sol_pi, divider, sol_dp], axis=0)
print("\nSolutions Ground Truth (top), PINN (middle) , DiffPhys (bottom):")
show_state(np.reshape(sbs,[N*3+20,33,1]))
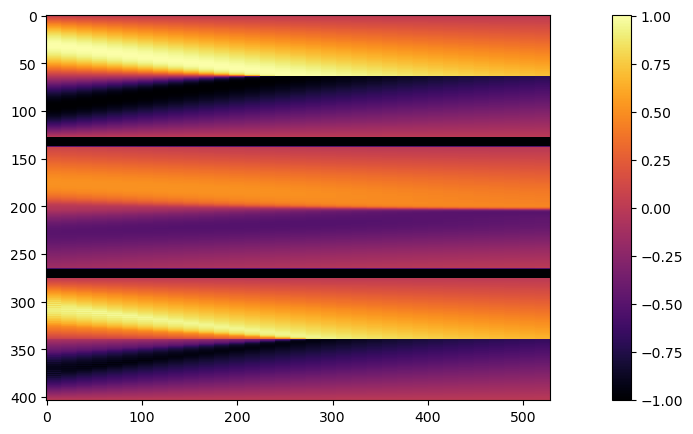
在这里很明显可以看到,PINN解决方案(中间)恢复了解的整体形状,因此时间约束至少部分得到满足。然而,它并没有很好地捕捉到GT解决方案的幅值。
与可微分求解器的优化重建(底部)相比,由于整个序列的梯度流改善,它更接近于真实情况。此外,它可以利用基于网格的离散化进行正向和反向传递,并以这种方式向未知的初始状态提供更准确的信号。然而,可以看出重建缺少GT版本的某些“更锐利”的特征,例如在解图像的左下角可见。
让我们量化整个序列的误差:
err_pi = np.sum( np.abs(sol_pi-sol_gt)) / (STEPS*N)
err_dp = np.sum( np.abs(sol_dp-sol_gt)) / (STEPS*N)
print("MAE PINN: {:7.5f} \nMAE DP: {:7.5f}".format(err_pi,err_dp))
print("\nError GT to PINN (top) , GT to DiffPhys (bottom):")
show_state(np.reshape( np.concatenate([sol_pi-sol_gt, divider, sol_dp-sol_gt],axis=0) ,[N*2+10,33,1]))
执行结果:
MAE PINN: 0.19298
MAE DP: 0.06382
Error GT to PINN (top) , GT to DiffPhys (bottom):
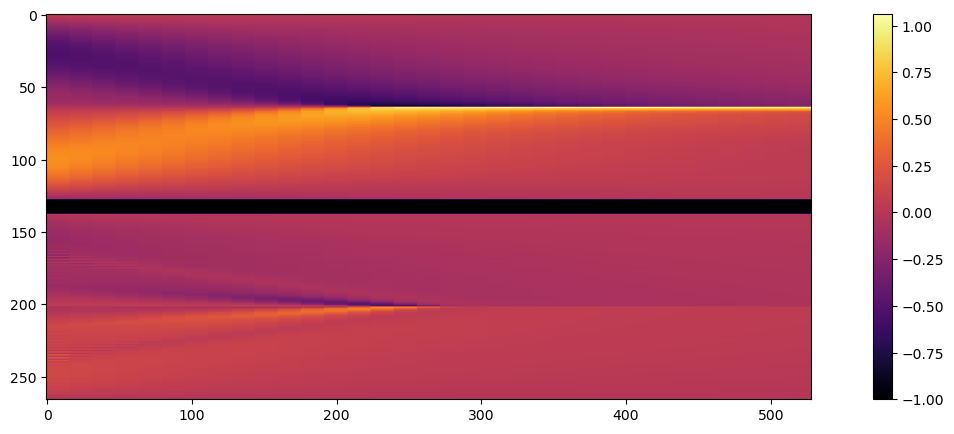
这是一个相当清晰的结果:PINN误差比可微物理(DP)重建的误差大3倍以上。
这个差异在底部的联合可视化图像中也清晰可见:DP重建的误差幅度更接近于零,如上方的紫色所示。
像这样的简单直接重建问题对于DP求解器来说总是一个很好的初始测试。在进入更复杂的设置(例如与NN耦合)之前,可以独立测试它。如果直接优化无法收敛,可能仍然存在一些根本性问题,没有必要涉及NN。
现在我们有了一个第一个示例来展示这两种方法的相似性和差异。在下一节中,我们将对迄今为止的发现进行讨论,然后在下一章中转向更复杂的情况。
8.6 下一步
与之前一样,可以使用上述代码改进和进行实验的事物有很多:
- 可以尝试调整训练参数以进一步改善重建效果。
- 激活不同的优化器,并观察收敛行为的变化(不一定是改善)。
- 改变步数或模拟和重建的分辨率。
- 尝试在
loss_function之前的一行添加@jit_compile。这将增加一次编译成本,但极大地加快了优化的速度。
在前面的章节中, 我们看到了一些使用物理残差作为软约束的重构示例, 采用的是变体 2 (PINN)的形式, 以及采用不同 iable 物理 (DP)求解器的重构。虽然两种方法都可以为类似的逆问题找到最小化方案, 但获得的解决方案差异很大, 从每个公式得到的非线性优化问题的行为也有很大不同。在下面, 我们更详细地讨论这些差异, 并将从{doc} physicalloss-code 和{doc} diffphys-code-burgers 的博格方程案例的行为中得出的结论与来自外部研究论文{cite} holl2019pdecontrol 的观察结合起来。
在前一节中,我们已经看到了使用物理残差作为软约束(变体2(PINNs)的形式)的重构示例,并使用了可微分物理(DP)求解器的重建。虽然这两种方法都能为类似的逆问题找到最小值,但得到的解却大相径庭,我们从每种表述中得到的非线性优化问题的行为也不尽相同。接下来,我们将更详细地讨论这些差异,并将结合从Burgers案例的行为中得出的结论Burgers Optimization with a Physics-Informed NN 及 Burgers Optimization with a Differentiable Physics Gradient,以及来自外部研究论文的观察结果 [HKT19]。

9.1 与现有数值方法的兼容性
很明显,PINN 的实现非常简单,这是一个积极的方面,但与此同时,它与 典型的离散化和求解方法有很大不同,后者通常用于求解Burgers方程等 PDE。其导数是通过神经网络计算的,因此依赖于相当精确的解的表示,从而为优化问题提供一个良好的方向。
另一方面,DP 版本本质上依赖于与学习过程联系在一起的数值求解器。因此,它需要将要处理的问题离散化,并通过这种离散化采用现有的、潜在的强大数值技术。这意味着解法和导数可以以已知和可控的精度进行评估,而且评估效率很高。
9.2 离散化
对于适当离散化的依赖需要对所考虑的问题有一定的理解和知识。次优的离散化可能会阻碍学习过程,甚至最糟糕的情况是导致训练过程发散。然而,鉴于大量理论和实际稳定求解器在各种物理问题上的实现,这通常并不是一个无法克服的障碍。
另一方面,PINN方法不需要事先选择离散化,因此看起来是“无离散化”的。然而,这只是表面上的一个优势。由于它们在计算机中求解,它们自然必须对问题进行离散化。它们通过训练过程中的非线性优化来构建这种离散化,这个过程受到底层优化的限制,并且很难从外部进行控制。因此,结果的准确性取决于训练过程如何能够合理地估计问题的复杂性,并且训练数据如何逼近解的未知区域。
例如,正如在Burgers示例中所示,PINN解通常在时间上反向传播信息时存在显着困难。这与该方法的效率密切相关。
9.3 效率
PINN方法通常执行局部采样和解的修正,这意味着以权重更新的形式进行的修正通常也是局部的。在空间和时间上满足边界条件可能会相应地变慢,导致实际训练时间较长。
良好选择的DP方法离散化可以纠正这种行为,并提供改进的梯度信息流。同时,依赖计算网格意味着可以非常快速地获得解。给定一个插值格式或一组基函数,可以在计算网格的一个非常局部的邻域内的任何时空点采样解。最坏情况下,这可能导致轻微的内存开销,例如,通过重复存储解的大部分常数值。
另一方面,对于使用全连接网络的PINN表示,我们需要对整个网络中可能的大量值进行完整遍历,以获得单个点的解样本。网络实际上需要对完整的高维解进行编码,其大小也决定了导数计算的效率。
9.4 持续的效率
也就是说,由于DP方法可以涵盖更大的解空间,因此这些解空间的结构通常也难以学习。例如,当训练一个具有较多迭代次数(即对未来进行长期展望)的网络时,这通常代表着一个比短期展望更难学习的信号。
因此,这些训练过程不仅需要更多的计算资源来进行每个神经网络迭代,而且通常需要更长的时间才能收敛。关于资源,每次正向计算可能需要大量的仿真步骤,并且通常需要相似数量的资源用于反向传播步骤。因此,虽然它们在某些时候可能看起来代价高昂且收敛速度慢,但这通常是由需要学习的更复杂信号所引起的。

9.5 总结
下表总结了物理信息 (PI)和可微分物理 (DP)方法的这些优缺点:
| 方法 | ✅ 优点 | ❌ 缺点 |
|---|---|---|
| PI | 通过反向传播解析导数。 | 评估神经网络非常昂贵, 导数计算代价极其高昂。 |
| 实现简单。 | 与现有数值方法不兼容。 | |
| 对离散化过程无法控制。 | ||
| DP | 利用现有数值方法。 | 实现较复杂。 |
| 求解模拟和导数计算效率高。 | 需要对问题有一定了解以选择合适的离散化格式。 | |
总之,这两种方法都非常有趣,并且具有很大的潜力。有许多更复杂的扩展和算法修改可以改变和改进我们讨论过的两种方面的缺点。
然而,就目前而言,基于物理的方法在性能和与现有数值方法的兼容性方面存在明显的局限性。因此,当我们了解所处理问题的知识时,通常情况下我们会选择一个适当的偏微分方程模型来约束学习过程,采用可微分的物理求解器可以显著改善训练过程以及获得的解的质量。因此,在接下来的内容中,我们将重点关注不同DP求解器的变体,并在下一章中用更复杂的场景来说明它们的能力。首先,我们将考虑一种非常高效地计算瞬态流体模拟的时空梯度的情况。
我们现在以Navier-Stokes方程作为物理模型来考虑一个更复杂的例子。根据 Navier-Stokes Forward Simulation,我们将考虑一个二维情况。
作为优化目标,我们将考虑前面Burgers方程例子的一个更困难的变体:观测到的密度在经过步模拟后应与给定的目标匹配。与之前不同的是,以标记场的形式观测到的量不能以任何方式改变。只能修改时速度的初始状态。这给了我们在损失函数表达中可观测量和在优化过程中(或之后通过神经网络)可以进行交互的量之间的分离。
10.1 物理模型
我们将使用无粘性Navier-Stokes模型,其中包含速度,没有显式的粘度项,并且有一个烟雾标记密度,它驱动一个简单的Boussinesq浮力项,在y维度上添加一个力。由于缺乏显式粘度,这些方程等价于欧拉方程。因此,我们得到:
以及被动运移标记密度 的额外的输运方程:
10.2 形式化
使用2 概述 中的符号表示法,上述逆问题可以表述为最小化问题
在目标时间处,是参考解的样本,而表示我们模拟器在相同采样位置和时间的估计值。这里的索引遍历流体求解器中所有离散化的空间自由度(下面我们将使用)。
与以前不同的是,我们不再处理预先计算的数量,而是现在本身是一个复杂的非线性函数。更具体地说,模拟器从初始速度和密度开始,通过对离散化的PDE 进行次评估来计算。这给出了模拟的最终状态,在接下来的过程中,我们将保持不变,将重点放在上作为我们的自由度。
因此,优化只能改变 以尽可能准确地使 与参考值 对齐。
10.3 开始实现
首先,让我们先处理Python模块的加载。通过导入phi.torch.flow,我们可以获得在PyTorch中工作并能够提供梯度的流体模拟函数(对于TensorFlow,可以选择使用phi.tf.flow)。
!pip install --upgrade --quiet phiflow==2.2
from phi.torch.flow import *
import pylab # for visualizations later on
10.4 批量模拟
现在我们可以设置模拟,该模拟将与之前的“常规”模拟示例(来自{doc}overview-ns-forw)保持一致。然而,现在我们将直接包含一个额外的维度,类似于用于神经网络训练的小批量。为此,我们将引入一个名为inflow_loc的命名维度。这个维度将存在于之前的空间维度y、x之上,这些维度被声明为vector通道的维度。正如inflow_loc这个名字所示,这个维度的主要区别在于入流的不同位置,以获得不同的流动模拟。在phiflow中的命名维度使得在不同张量的匹配维度之间广播信息非常方便。
# closed domain
INFLOW_LOCATION = tensor([(12, 4), (13, 6), (14, 5), (16, 5)], batch('inflow_loc'), channel(vector="x,y"))
INFLOW = (1./3.) * CenteredGrid(Sphere(center=INFLOW_LOCATION, radius=3), extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
BND = extrapolation.ZERO # closed, boundary conditions for velocity grid below
# uncomment this for a slightly different open domain case
#INFLOW_LOCATION = tensor([(11, 6), (12, 4), (14, 5), (16, 5)], batch('inflow_loc'), channel(vector="x,y"))
#INFLOW = (1./4.) * CenteredGrid(Sphere(center=INFLOW_LOCATION, radius=3), extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
#BND = extrapolation.BOUNDARY # open boundaries
INFLOW.shape
输出结果:
(inflow_locᵇ=4, xˢ=32, yˢ=40)
最后一条语句验证我们的 INFLOW 网格同样具有 inflow_loc 维度,以及空间维度 x 和 y。您可以在 phiflow 中使用 .exists 布尔值来测试张量维度的存在。例如,上述 INFLOW.inflow_loc.exists 将给出 True,而 INFLOW.some_unknown_dim.exists 将给出 False。上标 表示 inflow_loc 是一个批量维度。
Phiflow 张量会通过其名称自动广播到新维度,因此通常不需要重新塑形操作。例如,您可以轻松添加或乘以具有不同维度的张量。在下面,我们将一个交错网格与沿 inflow_loc 维度的全 1 张量相乘,通过 StaggeredGrid(...) * math.ones(batch(inflow_loc=4)) 得到一个具有 x,y,inflow_loc 作为维度的交错速度场。
现在我们可以轻松地从这些不同的初始条件模拟几步。由于广播,我们在概述章节中用于单前向模拟的完全相同的代码将产生四个模拟,具有不同的烟雾进流位置。
smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40))) # sampled at cell centers
velocity = StaggeredGrid(0, BND, x=32, y=40, bounds=Box(x=(0,32), y=(0,40))) # sampled in staggered form at face centers
def step(smoke, velocity):
smoke = advect.mac_cormack(smoke, velocity, dt=1) + INFLOW
buoyancy_force = (smoke * (0, 1)).at(velocity)
velocity = advect.semi_lagrangian(velocity, velocity, dt=1) + buoyancy_force
velocity, _ = fluid.make_incompressible(velocity)
return smoke, velocity
for _ in range(20):
smoke,velocity = step(smoke,velocity)
# store and show final states (before optimization)
smoke_final = smoke
fig, axes = pylab.subplots(1, 4, figsize=(10, 6))
for i in range(INFLOW.shape.get_size('inflow_loc')):
axes[i].imshow(smoke_final.values.numpy('inflow_loc,y,x')[i,...], origin='lower', cmap='magma')
axes[i].set_title(f"Inflow {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}" + (", Reference" if i==3 else ""))
pylab.tight_layout()
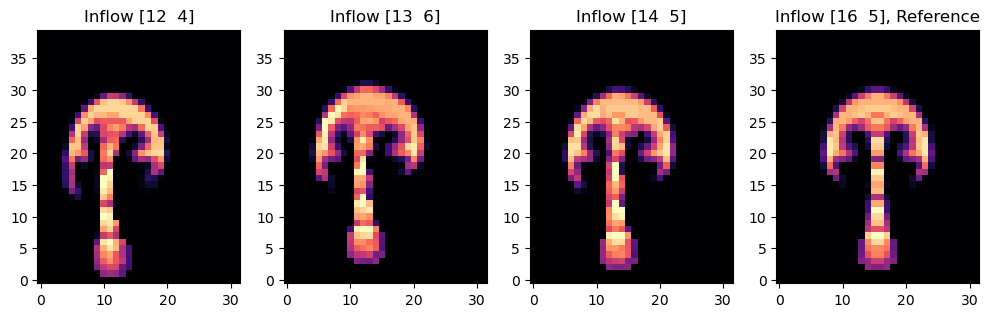
注:这里若报告
“OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.”错误,可在最前面指定环境变量:import os os.environ['KMP_DUPLICATE_LIB_OK']='True'
最后一张图展示了经过20步模拟后,流场中烟雾的状态。模拟[3]中的最终烟雾形状,在右侧有一个直立的烟囱,将作为我们下面的参考状态。其他三个模拟的初始速度将在下面的优化过程中进行修改,以匹配这个参考状态。
(作为一个小的附注:phiflow张量将使用它们创建时的后端来跟踪它们的操作链。例如,使用NumPy创建的张量将继续使用NumPy/SciPy的操作,除非同时传递给相同操作的PyTorch或TensorFlow张量。因此,定期验证张量是否使用了正确的后端是一个好主意,例如通过GRID.values.default_backend。)
梯度
让我们看看如何从我们的模拟中获取梯度。上面已经处理的第一个简单的步骤是包含 phi.torch.flow 来导入可微分算子以构建我们的模拟器。
现在我们想要优化初始速度,使得所有模拟都到达一个类似于右侧模拟的最终状态,其中入口位于 (16, 5),即沿 x 居中。为了实现这一点,我们在模拟过程中记录梯度,并定义一个简单的基于 的损失函数。我们将使用的损失函数由 给出,其中 表示烟密度, 表示我们批处理中第四个模拟的参考状态(均在最后时间步 评估)。在评估损失函数时,我们将参考状态视为外部常量,通过 field.stop_gradient() 处理。正如上面所述, 是 的函数(通过平流方程),而 又由 Navier-Stokes 方程给出。因此,通过多个时间步的链式关系, 取决于初始速度状态 。
重要的是,在记录梯度之前,我们的初始速度具有 inflow_loc 维度,以便我们具有完整的速度“小批量”(其中三个将在后续优化中通过梯度更新)。为了获得适当的速度张量,我们使用零张量初始化一个 StaggeredGrid,沿着 inflow_loc 批处理维度。由于交错网格已经具有 y,x 和 vector 维度,因此这给出了所需的四个维度,如下面的打印语句所验证的。
Phiflow 通过使用需要返回损失值以及可选状态值的函数,在不同平台上提供了统一的梯度 API。它使用基于损失函数的接口,我们在下面定义了 simulate 函数。simulate 计算上述 误差,并在 20 个模拟步骤后返回演化的 smoke 和 velocity 状态。
initial_smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
initial_velocity = StaggeredGrid(math.zeros(batch(inflow_loc=4)), BND, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
print("Velocity dimensions: "+format(initial_velocity.shape))
def simulate(smoke: CenteredGrid, velocity: StaggeredGrid):
for _ in range(20):
smoke,velocity = step(smoke,velocity)
loss = field.l2_loss(smoke - field.stop_gradient(smoke.inflow_loc[-1]) )
# optionally, use smoother loss with diffusion steps - no difference here, but can be useful for more complex cases
#loss = field.l2_loss(diffuse.explicit(smoke - field.stop_gradient(smoke.inflow_loc[-1]), 1, 1, 10))
return loss, smoke, velocity
输出结果:
Velocity dimensions: (inflow_locᵇ=4, xˢ=32, yˢ=40, vectorᶜ=x,y)
Phiflow的field.functional_gradient()函数是计算梯度的核心函数。接下来,我们将使用它来获取相对于初始速度的梯度。由于速度是simulate()函数的第二个参数,我们传递wrt=[1]。(Phiflow还有一个field.spatial_gradient函数,它计算张量沿空间维度(如x,y)的导数。)
functional_gradient生成一个梯度函数。作为演示,下一个单元格使用烟雾和速度的初始状态评估梯度一次。最后一条语句打印了结果梯度张量的部分摘要。
sim_grad = field.functional_gradient(simulate, wrt=[1], get_output=False)
(velocity_grad,) = sim_grad(initial_smoke, initial_velocity)
print("Some gradient info: " + format(velocity_grad))
print(format(velocity_grad.values.inflow_loc[0].vector[0])) # one example, location 0, x component, automatically prints size & content range
输出结果:
Some gradient info: StaggeredGrid[(inflow_locᵇ=4, xˢ=32, yˢ=40, vectorᶜ=x,y), size=(x=32, y=40) int64, extrapolation=0]
(xˢ=31, yˢ=40) 2.61e-08 ± 8.5e-01 (-2e+01...1e+01)
最后两行代码只是打印了一些关于生成的梯度场的信息。自然地,它的形状与速度本身相同:它是一个带有四个流入位置的交错网格。最后一行展示了如何访问其中一个梯度的x分量。
我们可以使用常规的绘图函数来查看计算得到的梯度的内容,例如,通过将其中一个模拟的x分量转换为numpy数组,使用velocity_grad.values.inflow_loc[0].vector[0].numpy('y,x')。另一种交互式的选择是使用phiflow的view()函数,它会自动分析网格内容并提供UI按钮来选择不同的查看模式。您可以使用它们来显示箭头、二维速度向量的单个分量或者它们的大小。由于它的交互性质,对应的图像不会在Jupyter之外显示,因此我们通过plot()来显示下面的向量长度。
# neat phiflow helper function:
vis.plot(field.vec_length(velocity_grad)) # show magnitude
输出结果:
<Figure size 864x360 with 5 Axes>

毫不奇怪,左侧的第四个梯度为零(它已经与参考值相匹配)。其他三个梯度已检测到初始回流位置的变化,表现为围绕回流的圆形形状的正负区域。左侧较大距离的梯度也明显更大。
优化
上面可视化的梯度只是指向增加损失的线性化变化。现在我们可以通过更新初始速度的相反方向来最小化损失,并迭代寻找最小值。
这是一个困难的任务:由于不同的初始空间密度配置,模拟产生了不同的动力学。我们的优化现在应该找到一个单一的初始速度状态,使得在时与参考模拟具有相同的状态。因此,在进行20个非线性更新步骤后,模拟应该能够再现所需的标记密度状态。要达到这个目标,只需改变标记流入的位置会更容易,但为了使事情更困难和有趣,流入不是自由度。优化器只能改变初始速度。
下面的单元格实现了一个简单的最陡梯度下降优化:重新评估梯度函数,并迭代多次以使用学习率(步长)LR优化。
field.functional_gradient有一个参数get_output,确定是否返回函数的原始结果(在我们的例子中为simulate())或仅返回梯度。由于追踪损失在迭代过程中的演变是有趣的,让我们重新定义带有get_output=True的梯度函数。
sim_grad_wloss = field.functional_gradient(simulate, wrt=[1], get_output=True) # if we need outputs...
LR = 1e-03
for optim_step in range(80):
(loss, _smoke, _velocity), (velocity_grad,) = sim_grad_wloss(initial_smoke, initial_velocity)
initial_velocity = initial_velocity - LR * velocity_grad
if optim_step<3 or optim_step%10==9: print('Optimization step %d, loss: %f' % (optim_step, np.sum(loss.numpy()) ))
输出:
Optimization step 0, loss: 298.286163
Optimization step 1, loss: 291.454102
Optimization step 2, loss: 276.057861
Optimization step 9, loss: 235.939117
Optimization step 19, loss: 211.866379
Optimization step 29, loss: 186.080994
Optimization step 39, loss: 170.441772
Optimization step 49, loss: 181.928848
Optimization step 59, loss: 181.899567
Optimization step 69, loss: 164.614792
Optimization step 79, loss: 161.756241
损失应该显著下降,从近300降至170以下,现在我们还可以可视化在优化中获得的初始速度。
以下图像显示了三个初始速度的结果,分别是它们的x分量(第一组图像)和y分量(第二组图像)。我们跳过了第四组图像,即inflow_loc[0],因为它只包含零。
fig, axes = pylab.subplots(1, 3, figsize=(10, 4))
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
im = axes[i].imshow(initial_velocity.staggered_tensor().numpy('inflow_loc,y,x,vector')[i,...,0], origin='lower', cmap='magma')
axes[i].set_title(f"Ini. vel. X {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
pylab.colorbar(im,ax=axes[i])
pylab.tight_layout()
fig, axes = pylab.subplots(1, 3, figsize=(10, 4))
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
im = axes[i].imshow(initial_velocity.staggered_tensor().numpy('inflow_loc,y,x,vector')[i,...,1], origin='lower', cmap='magma')
axes[i].set_title(f"Ini. vel. Y {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
pylab.colorbar(im,ax=axes[i])
pylab.tight_layout()
重新模拟
我们还可以可视化模拟在20步的完整过程,考虑到每个流入位置的新初始速度条件。这就是在每次梯度计算时优化过程内部发生的情况,也是我们的损失函数所测量的。因此,了解优化算法找到了哪些解是很有帮助的。
下面,我们使用initial_velocity中的新初始条件重新运行正向模拟:
smoke = initial_smoke
velocity = initial_velocity
for _ in range(20):
smoke,velocity = step(smoke,velocity)
fig, axes = pylab.subplots(1, 4, figsize=(10, 6))
for i in range(INFLOW.shape.get_size('inflow_loc')):
axes[i].imshow(smoke_final.values.numpy('inflow_loc,y,x')[i,...], origin='lower', cmap='magma')
axes[i].set_title(f"Inflow {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}" + (", Reference" if i==3 else ""))
pylab.tight_layout()

自然地,右边的图像是相同的(这是参考图像),而其他三个模拟现在向右偏移。由于差异有点微妙,让我们可视化目标配置与不同最终状态之间的差异。
以下图像显示了演化模拟和目标密度之间的差异。因此,暗区域表示目标应该出现但没有出现的地方。顶行显示了初始速度为零的原始状态,而底行显示了经过优化调整初始速度后的版本。因此,在每一列中,您可以比较之前(顶部)和之后(底部)的情况。
fig, axes = pylab.subplots(2, 3, figsize=(10, 6))
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
axes[0,i].imshow(smoke_final.values.numpy('inflow_loc,y,x')[i,...] - smoke_final.values.numpy('inflow_loc,y,x')[3,...], origin='lower', cmap='magma')
axes[0,i].set_title(f"Org. diff. {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
pylab.colorbar(im,ax=axes[0,i])
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
axes[1,i].imshow(smoke.values.numpy('inflow_loc,y,x')[i,...] - smoke_final.values.numpy('inflow_loc,y,x')[3,...], origin='lower', cmap='magma')
axes[1,i].set_title(f"Result {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
pylab.colorbar(im,ax=axes[1,i])
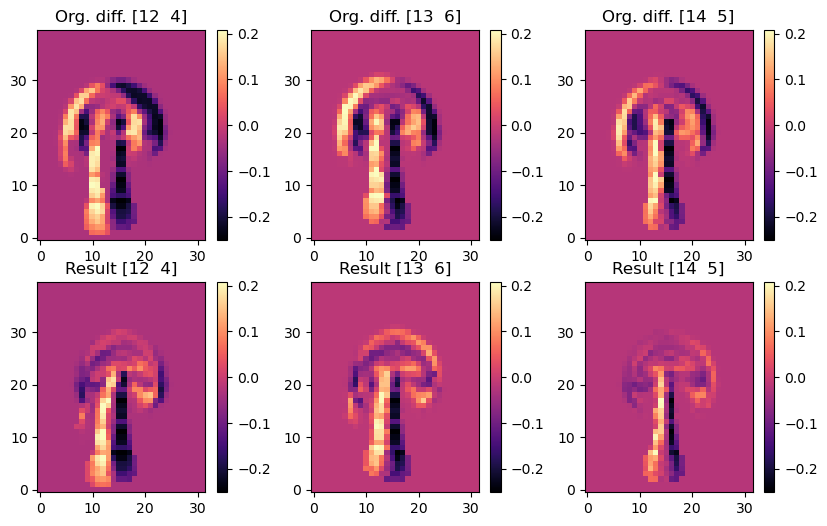
这些差异图清晰地显示出优化成功地对齐了烟羽的上部区域。每个原始图像(顶部)都显示出明显的不对齐,即黑色光晕,而优化后的状态在很大程度上与参考的目标烟雾配置重叠,并且在每个烟云的前部展示出更接近零的差异。
需要注意的是,所有三个模拟都需要与固定的流入进行“配合”,因此它们不能仅仅“凭空”产生标记密度以匹配目标。此外,每个模拟还需要考虑非线性模型方程如何在20个时间步骤内改变系统状态。因此,优化目标非常困难,在这种情况下,无法完全满足约束条件以匹配参考模拟。例如,这在烟羽的茎部是明显的,优化后仍然显示出黑色的光晕。优化无法改变流入位置,因此需要专注于对齐烟羽的上部区域。
结论
这个例子说明了可微分物理方法如何轻松地扩展到更加复杂的偏微分方程。如上所述,我们已经对一个完整的Navier-Stokes求解器进行了20个步骤的小批量优化。
这为将神经网络引入图像提供了强大的基础。正如你可能已经注意到的,我们的自由度仍然是一个常规的网格,并且我们共同解决了一个单一的反问题。当然,需要解决三个案例作为小批量,但尽管如此,这个设置仍然代表了一个直接的优化过程。因此,与{doc}physicalloss-code中的PINN示例一致,我们在这里并没有真正处理一个“机器学习”任务。然而,DP训练允许与神经网络进行各种灵活的组合,这将是下一章的主题。
下一步
基于上述的代码示例,我们可以推荐尝试以下实验:
- 修改模拟的设置,使其在四个实例之间的差异更加明显,运行时间更长,或者使用更细的空间离散化(即更大的网格尺寸)。请注意,这将使优化问题更加困难,因此可能无法通过这个简单的设置直接收敛。
- 作为一个更大的改变,添加多分辨率优化来处理具有更大差异的情况。即,首先使用粗糙的离散化求解,然后将此解作为更细的离散化的初始猜测。
我们现在将重点放在将可微分物理(DP)设置与NN集成的方面。在使用DP方法进行学习应用时,关于DP和NN构建块的组合有很大的灵活性。由于一些差别非常微妙,下一节将更详细地讨论这些差别。我们将特别关注重复PDE和NN评估多次的求解器,例如,计算物理系统随时间变化的多个状态。
回顾一下,这是关于将NN和DP运算符相结合图示。在图中,这些运算符看起来像是一个损失项:它们通常没有权重,只提供一个梯度,影响NN权重的优化:
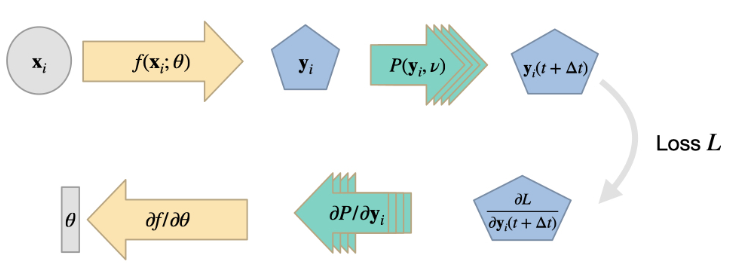
这个设置可以被视为网络接收关于其输出如何影响PDE求解器结果的信息。即梯度将提供如何生成最小化损失的神经网络输出的信息。类似于之前描述的"物理损失"(来自{doc}physicalloss),这可能意味着维持守恒定律。
这种设置可以看作是网络接收了关于其输出如何影响 PDE 求解器结果的信息。也就是说梯度将提供如何产生 NN 输出以最小化损失的信息。与之前描述的物理损失)类似,这可能意味着要坚持守恒定律。
11.1 更改顺序
但是,对于 DP 来说,我们没有理由局限于这种设置。例如,我们可以设想将 NN 和 DP 交换,从而得到以下结构:
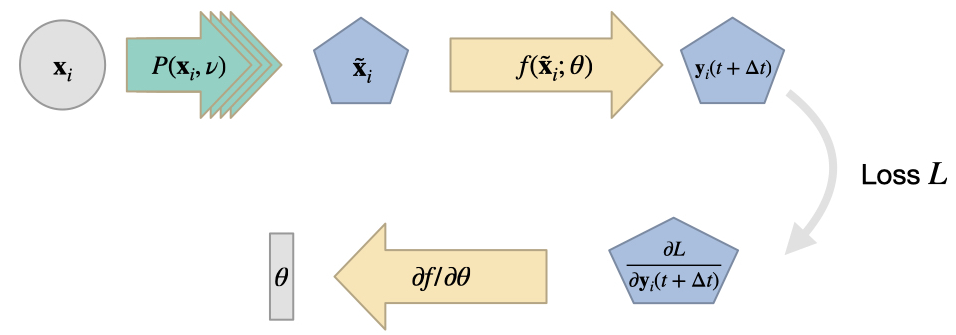
在这种情况下,PDE求解器本质上代表了一个即时生成数据的工具。这并不一定总是有用的:可以通过对相同输入进行预计算来替代这种设置,因为PDE求解器不受神经网络的影响。因此没有反向传播,可以被一个简单的"加载"函数替代。另一方面,在训练时使用随机采样的输入参数评估PDE求解器可以很好地对输入数据分布进行采样。如果我们对输入的变化范围有现实的了解,这可以改善神经网络的训练。如果正确实现,求解器还可以减轻存储和加载大量数据的需求,而是在训练时更快地生成这些数据,例如直接在GPU上生成。
然而,这个版本没有利用可微分求解器的梯度信息,这就是为什么下面的变体更加有趣的原因。
11.2 循环评估
一般来说,只要维度相容,没有任何NN层和DP操作符的组合是“禁止”的。其中一个特别有意义的组合是将模拟器的时间步进过程的迭代“展开”,并让系统的状态受到NN的影响。
在这种情况下,我们在正向传递中计算一系列(可能非常长)的PDE求解器步骤。在这些求解器步骤之间,NN修改系统的状态,然后用于计算下一个PDE求解器步骤。在反向传播过程中,我们通过所有这些步骤向后移动,以评估对损失函数的贡献(可以在执行链中的一个或多个位置进行评估),并通过DP和NN操作符反向传播梯度信息。这种求解器迭代的展开实际上向NN提供了关于其“行动”如何影响物理系统状态和损失的反馈。以下是这种组合形式的可视化概述:
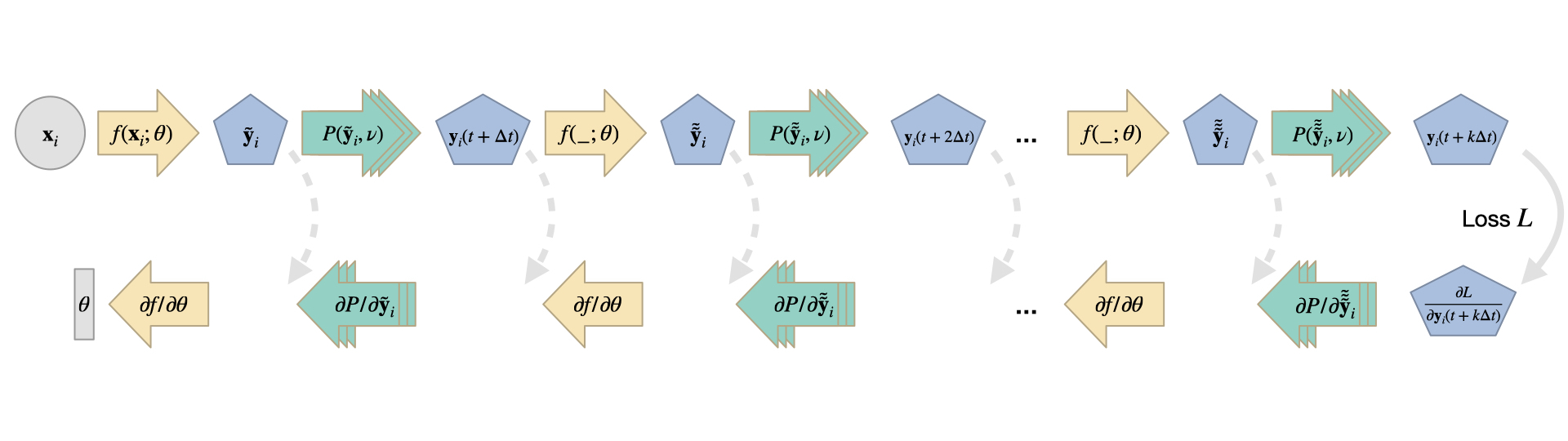
由于这个过程的迭代性质,错误一开始很小,然后在迭代过程中呈指数增长。因此,在单次评估中很难检测到这些错误,例如,在一个简单的监督训练设置中。相反,至关重要的是在训练时向神经网络提供有关错误如何随迭代过程而演变的反馈。此外,对于这种迭代的情况,无法进行状态的预计算,因为迭代取决于神经网络的状态。自然地,在训练之前,神经网络的状态是未知的,并且在训练过程中会发生变化。因此,在这些循环设置中,基于动态规划的训练对于向神经网络提供关于其当前状态如何影响求解器迭代以及相应地如何调整权重以更好地实现学习目标的梯度至关重要。
具有许多时间步的DP设置可能很难训练:梯度需要通过PDE求解器评估和神经网络评估的完整链路进行反向传播。通常,每个评估都代表一个非线性和复杂的函数。因此,对于更多步,梯度消失和梯度爆炸问题可能会导致训练困难。关于缓解这个问题的一些实际考虑将在 Reducing Numerical Errors with Deep Learning 中介绍。

11.3 NN 和求解器的组成
迄今为止,我们忽略了一个问题,即如何将神经网络的输出合并到迭代求解过程中。在上述图像中,神经网络似乎产生了物理系统的完整状态,并被用作的输入。这意味着对于步骤处的状态,神经网络产生了一个中间状态,求解器利用该状态生成下一步的新状态:。
虽然这种方法是可行的,但并不一定在所有情况下都是最佳选择。特别是如果神经网络只应该对当前状态进行修正,我们可以重用当前状态的部分。这样可以避免将神经网络的资源分配给已经正确的部分,即的某些部分。类似于U-Net的跳跃连接和ResNet的残差,这种情况下最好使用一个运算符来合并和,即。
在最简单的情况下,我们可以定义为加法,此时表示对的加性修正。简言之,我们通过评估来计算下一个状态。在这种情况下,网络只需要更新尚未满足学习目标的的部分。
一般来说,我们可以使用任何可微的运算符,它可以是乘法或积分方案。与损失函数类似,这个选择取决于具体问题,但加法通常是一个很好的起点。
11.4 方程形式
接下来,我们将正式描述前面段落中的内容。具体来说,我们将回答一个问题:对于雅可比矩阵,的更新步骤是什么样子的?给定一个带有索引的小批次和一个损失函数,我们将使用表示迭代中展开的总步数。为了缩短符号表示,表示在时间步时,批次的的状态。
利用这个符号表示,我们可以将网络权重的梯度写成:
乍一看,这个表达式似乎不太直观,但其结构相当简单:第一个求和式对于 累加了一个小批量中的所有条目。然后我们有一个对 (括号)的外部求和,涵盖了从 到 的所有时间步骤。对于每个 ,我们将沿着从最终状态 到每个 的链路追踪,通过沿途乘以所有雅可比矩阵(用索引 表示,括在括号中)来实现。沿途的每一步都由每个时间步长相对于 的雅可比矩阵组成,而这又取决于来自 NN 的修正(未写出)。
在神经网络的每个最后一步 ,我们“分支出”,确定在第 个时间步长时网络输出 和其权重 的变化。所有这些对于不同的 的贡献都被加起来,形成一个最终更新 ,用于我们训练过程中的优化器。
需要记住的是,对于大的 , 和 的递归应用的雅可比矩阵强烈影响后续时间步骤的贡献,因此稳定训练以防止梯度爆炸尤为关键。这是一个我们稍后将多次重访的主题。
在实现方面,所有深度学习框架都会重复使用重叠部分,这些部分针对不同的 重复。这在反向传播评估中自动处理,在实践中,求和将从大到小的 进行评估,以便我们在向小的 移动时“忘记”后续步骤。因此,反向传播步骤确实增加了计算成本,但通常与前向传递的计算成本相当,前提是我们有适当的运算符来计算 的导数。
11.5 通过求解器步骤进行反向传播
既然我们已经设置好了所有这些机器,一个很好的问题是:“使用可微分的物理模拟器进行训练真的能够改善情况吗?我们是否可以简单地展开一个监督式的设置,类似于标准的递归训练,而不使用可微分的求解器?”或者换一种说法,我们通过求解器的多步反向传播到底能获得多少好处?
简而言之,相当多!下面的段落展示了来自List等人的湍流混合层的评估案例,以说明这种差异。在进入细节之前,值得注意的是,这种比较使用了一个可微分的二阶半隐式流动求解器和一组定制的湍流损失项。因此,这不是一个玩具问题,而是展示了可微分性对于复杂的真实案例的影响。
这个案例的好处是,我们可以根据湍流案例的已建立的统计测量来评估它,并以这种方式量化差异。流动的能谱通常是一个起点,但我们将跳过它,并参考原始论文,而是更加关注两个更具信息量的指标。下面的图表显示了雷诺应力和湍流动能(TKE),都是以流动中的横截面的已解决量表示。橙色点表示参考解。

尤其是在彩色箭头所指示的区域,"展开监督"训练的红色曲线与参考解决方案的偏离更为明显。这两个测量值是在使用流体求解器和经过训练的神经网络进行1024个时间步骤的模拟后进行的。因此,这两个解决方案都相当稳定,并且比求解器的未修改输出要好得多,这在图表中以蓝色显示。
当定性比较涡度场的可视化时,差异在视觉上也非常明显:
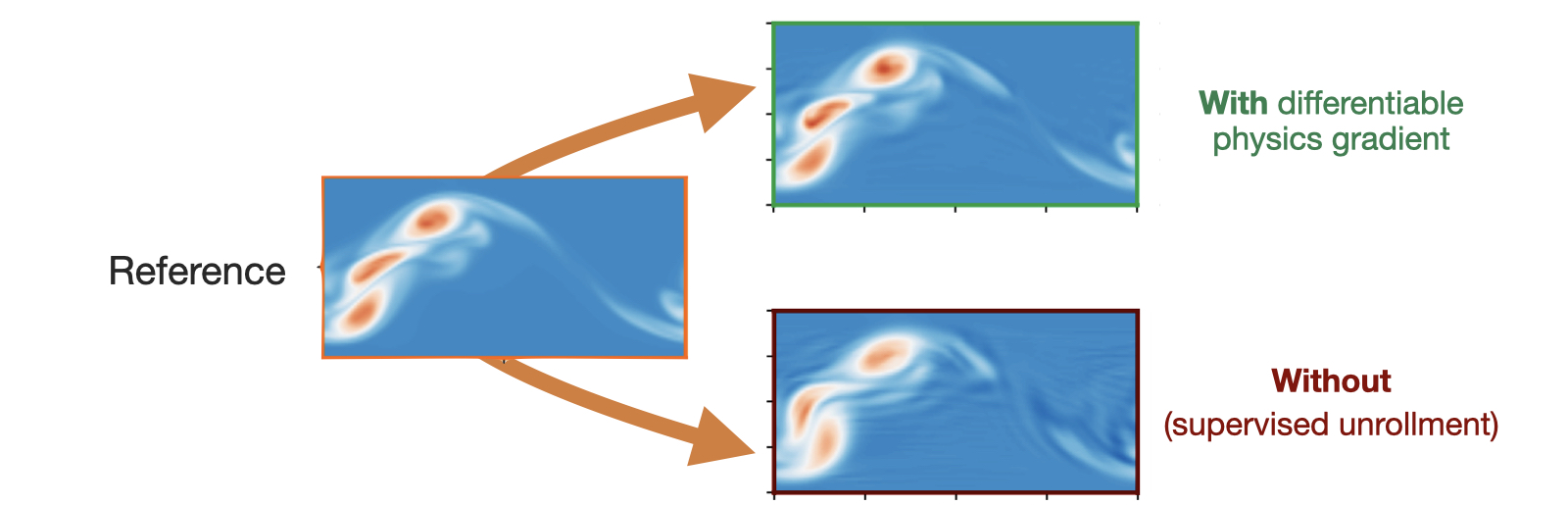
两个版本,有和无求解器梯度的版本,在这个比较中都极大地受益于展开,展开了10步。然而,没有动态规划的监督变体无法在训练时利用关于神经网络效果的长期信息,因此其能力受到限制。经过可微分求解器训练的版本在整个10步展开过程中都获得了反馈,并且通过这种方式可以推断出改进精度的校正,从而提高了由神经网络驱动的求解器的准确性。
展望未来,本案例还凸显了将 NN 纳入求解器的实际优势:我们可以测量常规模拟需要多长时间才能达到一定的湍流统计精度。在本例中,使用 NN {cite}"list2022piso "求解器所需时间是使用 NN"求解器所需时间的 14 倍以上。
虽然这只是第一个数据点,但我们很高兴地看到,一旦网络经过训练,或多或少就能在性能方面实现实际改进。
11.6 替代方法: 噪声
其他作品已经提出在训练时通过噪声扰动输入和迭代,这与像dropout这样的正则化器有些相似 {cite}sanchez2020learning。这可以帮助防止过度拟合训练状态,并且以这种方式可以帮助稳定训练迭代求解器。
然而,噪声的性质非常不同。它通常是无方向的,因此不如通过实际模拟演化进行训练准确。因此,噪声可以作为一个对于倾向于过度拟合的训练设置的良好起点。然而,如果可能的话,最好通过DP方法将实际求解器纳入训练循环中,以便网络可以获得关于系统时间演化的反馈。
11.7 复杂示例
下面的章节将给出更复杂情况的代码示例,以展示通过可微分物理训练可以实现什么。
首先,我们将按照Um等人的研究{cite}"um2020sol",展示一个利用深度学习来表示数值模拟误差的场景。这是一项非常基本的任务,需要学习到的模型与数值求解器密切互动。因此,在这种情况下,将数值求解器引入深度学习环路至关重要。
接下来,我们将展示如何让 NN 解决棘手的逆问题,即 Navier-Stokes 模拟的长期控制问题。这项任务需要长期规划,因此需要两个网络,一个预测演化,另一个采取行动以达到预期目标。(稍后,在 doc}reinflearn-code 中,我们将把这种方法与另一种使用强化学习的 DL 变体进行比较)。
这两种情况都比前面的例子需要更多的资源,所以你可以预期这些笔记本运行的时间会更长(在处理这些例子时,使用检查点是个好主意)。
在这个例子中,我们将针对在连续偏微分方程 离散化时出现的数值误差进行处理,即当我们构建 时。这种方法将证明,尽管缺乏封闭形式的描述,离散化误差通常是具有规则和重复结构的函数,因此可以通过神经网络进行学习。一旦网络训练完成,它可以在本地进行评估,以改善PDE求解器的解,即减少其数值误差。由此产生的方法是一种混合方法:它将始终运行(粗略的)PDE求解器,然后在运行时通过NN推断的修正来改进它。
几乎所有数值方法都包含某种形式的迭代过程:对于显式求解器,需要在时间上重复更新;对于隐式求解器,需要在单个更新步内进行迭代。第二种情况的示例可以在此处找到,但下面我们将针对第一种情况,即时间上的迭代。
12.1 问题表述
在减少误差的背景下,拥有一个可微分的物理求解器非常重要,这样学习过程才能考虑到求解器的反应。这种交互在监督学习或PINN训练中是不可能的。即使是监督型神经网络的小推理误差也会随着时间的推移而累积,并导致数据分布与预计算数据的分布不同。这种分布偏移会导致次优结果,甚至会导致求解器崩溃。
为了学习误差函数,我们将考虑同一偏微分方程的两种不同离散方式:一个我们认为准确的参考版本,具有离散化版本和解,其中表示的解流形。与此同时,我们有同一PDE的不太准确的近似,我们将其称为“源”版本,因为这将是我们的NN后来要与之交互的求解器。类似地,我们有和解。在训练后,我们将获得一个“混合”求解器,它使用与训练好的网络结合使用,以获得改进的解,即更接近产生的解。
假设通过时间步长推进了一个解,这里将个连续步骤表示为上标: 对应的模拟状态为 在这里,我们假设存在一个映射算子,其可以将参考解转移到源流形上。例如,这可以是一个简单的下采样操作。特别是对于较长的序列,即较大的,源状态将偏离相应的参考状态。这就是我们接下来将用NN解决的问题。
像以前一样, 我们将使用 范数来量化偏差, 即误差函数 。
我们的学习目标是训练一个校正算子 ,应用校正后的解比原始未经修改的 (源)解具有更低的误差: 。
修正函数 表示为具有权重 的深度神经网络,接收状态 并推断出具有相同维度的加性修正场。
为了区分原始状态 和修正后的状态,我们将后者用加了波浪线的符号 表示。现在,总体学习目标变为 为了简化符号,我们在此省略了对不同样本的求和(即以前版本中的 )。在上述方程中容易被忽视的关键部分是,修正取决于修改后的状态,即它是 的函数,因此我们有 。
这些状态在训练过程中实际上会随时间演化,它们事先并不存在。
我们将训练一个网络 来降低模拟器的数值误差,并使用更准确的参考进行训练。关键是将源求解器实现为微分物理运算符,以便为改进 的训练提供梯度。
12.2 开始实现
以下是从Solver-in-the-loop:从可微分物理学习与迭代PDE求解器交互 {cite}holl2019pdecontrol中复制的实验,更多细节可以在论文的附录B.1中找到(https://arxiv.org/pdf/2007.00016.pdf)。
首先,让我们下载准备好的数据集(有关生成和加载的详细信息,请参见https://github.com/tum-pbs/Solver-in-the-Loop),然后让我们解决数据处理问题,以便我们可以专注于“有趣”的部分...
import os, sys, logging, argparse, pickle, glob, random, distutils.dir_util, urllib.request
fname_train = 'sol-karman-2d-train.pickle'
if not os.path.isfile(fname_train):
print("Downloading training data (73MB), this can take a moment the first time...")
urllib.request.urlretrieve("https://physicsbaseddeeplearning.org/data/"+fname_train, fname_train)
with open(fname_train, 'rb') as f: data_preloaded = pickle.load(f)
print("Loaded data, {} training sims".format(len(data_preloaded)) )
执行结果:
Downloading training data (73MB), this can take a moment the first time...
Loaded data, 6 training sims
同时让我们安装/导入所有必要的库。我们设置随机种子,这里设置的是42。
!pip install --upgrade --quiet phiflow==2.2
from phi.tf.flow import *
import tensorflow as tf
from tensorflow import keras
random.seed(42)
np.random.seed(42)
tf.random.set_seed(42)
12.3 模拟设置
现在我们设置源模拟。请注意,我们不会在下面处理:下采样的参考数据包含在训练数据集中。它是用四倍的离散化生成的。下面,我们将重点关注源求解器和NN的交互。这个代码块和下一个代码块将定义许多函数,稍后将用于训练。
下面的KarmanFlow求解器模拟了一个相对标准的尾流情况,其中一个球形障碍物位于矩形域内,并使用显式粘度求解来获得不同的雷诺数。这是设置的几何形状:

求解器使用预乘掩码(vel_BcMask)为y-速度应用入流边界条件,以在模拟步骤期间设置域底部的y分量。该掩码是使用phiflow中的HardGeometryMask创建的,该掩码正确初始化了交错网格的分量的空间偏移条目。模拟步骤非常直接:它计算粘度、入流、对流的贡献,最后通过隐式压力求解使得结果运动无散。
class KarmanFlow():
def __init__(self, domain):
self.domain = domain
self.vel_BcMask = self.domain.staggered_grid(HardGeometryMask( Box(y=(None, 5), x=None) ) )
self.inflow = self.domain.scalar_grid(Box(y=(25,75), x=(5,10)) ) # scale with domain if necessary!
self.obstacles = [Obstacle(Sphere(center=tensor([50, 50], channel(vector="y,x")), radius=10))]
#
def step(self, density_in, velocity_in, re, res, buoyancy_factor=0, dt=1.0):
velocity = velocity_in
density = density_in
# viscosity
velocity = phi.flow.diffuse.explicit(field=velocity, diffusivity=1.0/re*dt*res*res, dt=dt)
# inflow boundary conditions
velocity = velocity*(1.0 - self.vel_BcMask) + self.vel_BcMask * (1,0)
# advection
density = advect.semi_lagrangian(density+self.inflow, velocity, dt=dt)
velocity = advected_velocity = advect.semi_lagrangian(velocity, velocity, dt=dt)
# mass conservation (pressure solve)
pressure = None
velocity, pressure = fluid.make_incompressible(velocity, self.obstacles)
self.solve_info = { 'pressure': pressure, 'advected_velocity': advected_velocity }
return [density, velocity]
12.4 网络架构
我们还将定义两个替代版本的神经网络来表示。在这两种情况下,我们将使用完全卷积网络,即没有任何全连接层的网络。我们将使用TensorFlow中的Keras来定义网络的层(主要通过Conv2D),分别使用ReLU和LeakyReLU函数进行激活。
网络的输入为:
- 带有x、y速度的2个场
- 雷诺数作为常量通道。
输出为:
- 包含x、y速度的2个分量场。
首先,让我们定义一个仅包含四个ReLU激活的卷积层的小型网络(为简单起见,我们也在这里使用Keras)。输入维度由inputs_dict中的输入张量确定(它有三个通道:u、v和Re)。然后,我们通过三个具有32个特征的卷积层处理数据,然后在输出中将通道减少到2个。
def network_small(inputs_dict):
l_input = keras.layers.Input(**inputs_dict)
block_0 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_input)
block_0 = keras.layers.LeakyReLU()(block_0)
l_conv1 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_0)
l_conv1 = keras.layers.LeakyReLU()(l_conv1)
l_conv2 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv1)
block_1 = keras.layers.LeakyReLU()(l_conv2)
l_output = keras.layers.Conv2D(filters=2, kernel_size=5, padding='same')(block_1) # u, v
return keras.models.Model(inputs=l_input, outputs=l_output)
为了灵活性(以及稍后进行更大规模的测试),让我们也定义一个更多层的“正式”的ResNet。这个架构是来自原始论文的,将会给出相当不错的性能(上面的network_small将会训练得更快,但是推理时间会给出次优的性能)。
def network_medium(inputs_dict):
l_input = keras.layers.Input(**inputs_dict)
block_0 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_input)
block_0 = keras.layers.LeakyReLU()(block_0)
l_conv1 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_0)
l_conv1 = keras.layers.LeakyReLU()(l_conv1)
l_conv2 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv1)
l_skip1 = keras.layers.add([block_0, l_conv2])
block_1 = keras.layers.LeakyReLU()(l_skip1)
l_conv3 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_1)
l_conv3 = keras.layers.LeakyReLU()(l_conv3)
l_conv4 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv3)
l_skip2 = keras.layers.add([block_1, l_conv4])
block_2 = keras.layers.LeakyReLU()(l_skip2)
l_conv5 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_2)
l_conv5 = keras.layers.LeakyReLU()(l_conv5)
l_conv6 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv5)
l_skip3 = keras.layers.add([block_2, l_conv6])
block_3 = keras.layers.LeakyReLU()(l_skip3)
l_conv7 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_3)
l_conv7 = keras.layers.LeakyReLU()(l_conv7)
l_conv8 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv7)
l_skip4 = keras.layers.add([block_3, l_conv8])
block_4 = keras.layers.LeakyReLU()(l_skip4)
l_conv9 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_4)
l_conv9 = keras.layers.LeakyReLU()(l_conv9)
l_convA = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv9)
l_skip5 = keras.layers.add([block_4, l_convA])
block_5 = keras.layers.LeakyReLU()(l_skip5)
l_output = keras.layers.Conv2D(filters=2, kernel_size=5, padding='same')(block_5)
return keras.models.Model(inputs=l_input, outputs=l_output)
接下来,我们要介绍两个非常重要的函数:它们将模拟状态转换为神经网络的输入张量,反之亦然。因此,它们是keras/tensorflow和phiflow之间的接口。
to_keras函数使用vector['x']和vector['y']中的两个向量分量来丢弃速度场网格的最外层层次。这样就得到了两个相等大小的张量,它们被连接在一起。然后,通过math.ones添加一个常量通道,该通道与ext_const_channel中所需的雷诺数相乘。结果的网格堆栈沿着channels维度堆叠,表示为神经网络的输入。
在网络评估之后,我们通过to_phiflow函数将输出张量转换回phiflow网格。它将网络返回的2分量张量转换为phiflow交错网格对象,以使其与流体模拟的速度场兼容。(注意:这是两个不同大小的_centered_网格,因此我们将工作留给domain.staggered_grid函数,该函数还根据域中给定的物理大小和边界条件进行设置)。
def to_keras(dens_vel_grid_array, ext_const_channel):
# align the sides the staggered velocity grid making its size the same as the centered grid
return math.stack(
[
math.pad( dens_vel_grid_array[1].vector['x'].values, {'x':(0,1)} , math.extrapolation.ZERO),
dens_vel_grid_array[1].vector['y'].y[:-1].values, # v
math.ones(dens_vel_grid_array[0].shape)*ext_const_channel # Re
],
math.channel('channels')
)
def to_phiflow(tf_tensor, domain):
return domain.staggered_grid(
math.stack(
[
math.tensor(tf.pad(tf_tensor[..., 1], [(0,0), (0,1), (0,0)]), math.batch('batch'), math.spatial('y, x')), # v
math.tensor( tf_tensor[...,:-1, 0], math.batch('batch'), math.spatial('y, x')), # u
], math.channel(vector="y,x")
)
)
12.5 数据处理
到目前为止一切都很好 - 我们还需要处理一些更加繁琐的任务,例如一些数据处理和随机化。下面我们定义一个Dataset类,它存储所有真值参考数据(已经进行了下采样)。实际上,我们有很多数据维度:多个模拟,有许多时间步长,每个时间步长都有不同的物理场。这使得下面的代码有点难以阅读。
numpy数组dataPreloaded的数据格式是['sim_name',frame,field(dens & vel)],其中每个场的维度为[batch-size,y-size,x-size,channels](这是phiflow导出的标准格式)。
class Dataset():
def __init__(self, data_preloaded, num_frames, num_sims=None, batch_size=1, is_testset=False):
self.epoch = None
self.epochIdx = 0
self.batch = None
self.batchIdx = 0
self.step = None
self.stepIdx = 0
self.dataPreloaded = data_preloaded
self.batchSize = batch_size
self.numSims = num_sims
self.numBatches = num_sims//batch_size
self.numFrames = num_frames
self.numSteps = num_frames
# initialize directory keys (using naming scheme from SoL codebase)
# constant additional per-sim channel: Reynolds numbers from data generation
# hard coded for training and test data here
if not is_testset:
self.dataSims = ['karman-fdt-hires-set/sim_%06d'%i for i in range(num_sims) ]
ReNrs = [160000.0, 320000.0, 640000.0, 1280000.0, 2560000.0, 5120000.0]
self.extConstChannelPerSim = { self.dataSims[i]:[ReNrs[i]] for i in range(num_sims) }
else:
self.dataSims = ['karman-fdt-hires-testset/sim_%06d'%i for i in range(num_sims) ]
ReNrs = [120000.0, 480000.0, 1920000.0, 7680000.0]
self.extConstChannelPerSim = { self.dataSims[i]:[ReNrs[i]] for i in range(num_sims) }
self.dataFrames = [ np.arange(num_frames) for _ in self.dataSims ]
# debugging example, check shape of a single marker density field:
#print(format(self.dataPreloaded[self.dataSims[0]][0][0].shape ))
# the data has the following shape ['sim', frame, field (dens/vel)] where each field is [batch-size, y-size, x-size, channels]
self.resolution = self.dataPreloaded[self.dataSims[0]][0][0].shape[1:3]
# compute data statistics for normalization
self.dataStats = {
'std': (
np.std(np.concatenate([np.absolute(self.dataPreloaded[asim][i][0].reshape(-1)) for asim in self.dataSims for i in range(num_frames)], axis=-1)), # density
np.std(np.concatenate([np.absolute(self.dataPreloaded[asim][i][1].reshape(-1)) for asim in self.dataSims for i in range(num_frames)], axis=-1)), # x-velocity
np.std(np.concatenate([np.absolute(self.dataPreloaded[asim][i][2].reshape(-1)) for asim in self.dataSims for i in range(num_frames)], axis=-1)), # y-velocity
)
}
self.dataStats.update({
'ext.std': [ np.std([np.absolute(self.extConstChannelPerSim[asim][0]) for asim in self.dataSims]) ] # Reynolds Nr
})
if not is_testset:
print("Data stats: "+format(self.dataStats))
# re-shuffle data for next epoch
def newEpoch(self, exclude_tail=0, shuffle_data=True):
self.numSteps = self.numFrames - exclude_tail
simSteps = [ (asim, self.dataFrames[i][0:(len(self.dataFrames[i])-exclude_tail)]) for i,asim in enumerate(self.dataSims) ]
sim_step_pair = []
for i,_ in enumerate(simSteps):
sim_step_pair += [ (i, astep) for astep in simSteps[i][1] ] # (sim_idx, step) ...
if shuffle_data: random.shuffle(sim_step_pair)
self.epoch = [ list(sim_step_pair[i*self.numSteps:(i+1)*self.numSteps]) for i in range(self.batchSize*self.numBatches) ]
self.epochIdx += 1
self.batchIdx = 0
self.stepIdx = 0
def nextBatch(self):
self.batchIdx += self.batchSize
self.stepIdx = 0
def nextStep(self):
self.stepIdx += 1
在训练时,nextEpoch、nextBatch和nextStep函数将被调用以随机化训练数据的顺序。
现在我们需要一个编译小批量数据以进行训练的函数,称为下面的getData。它以标记密度、速度和雷诺数的形式返回所需大小的批次。
# for class Dataset():
def getData(self, consecutive_frames):
d_hi = [
np.concatenate([
self.dataPreloaded[
self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]] # sim_key
][
self.epoch[self.batchIdx+i][self.stepIdx][1]+j # frames
][0]
for i in range(self.batchSize)
], axis=0) for j in range(consecutive_frames+1)
]
u_hi = [
np.concatenate([
self.dataPreloaded[
self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]] # sim_key
][
self.epoch[self.batchIdx+i][self.stepIdx][1]+j # frames
][1]
for i in range(self.batchSize)
], axis=0) for j in range(consecutive_frames+1)
]
v_hi = [
np.concatenate([
self.dataPreloaded[
self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]] # sim_key
][
self.epoch[self.batchIdx+i][self.stepIdx][1]+j # frames
][2]
for i in range(self.batchSize)
], axis=0) for j in range(consecutive_frames+1)
]
ext = [
self.extConstChannelPerSim[
self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]]
][0] for i in range(self.batchSize)
]
return [d_hi, u_hi, v_hi, ext]
请注意,这里的density指的是被动传递的标记场,而不是流体的密度。下面我们将仅关注速度,标记密度仅用于可视化目的进行跟踪。
在所有定义完成后,我们最终可以运行一些代码。我们使用第一个单元格下载的数据定义dataset对象。
nsims = 6
batch_size = 3
simsteps = 500
dataset = Dataset( data_preloaded=data_preloaded, num_frames=simsteps, num_sims=nsims, batch_size=batch_size )
程序输出:
Data stats: {'std': (2.6542656, 0.23155601, 0.3066732), 'ext.std': [1732512.6262166172]}
此外,我们定义了几个全局变量来控制下一个代码单元格中的训练和模拟。
其中最重要和有趣的是msteps。它定义了在每个训练迭代中展开的模拟步数。这直接影响每个训练步骤的运行时间,因为我们首先必须模拟所有步骤,然后通过所有与NN评估交替的msteps模拟步骤反向传播梯度。然而,这是我们将在梯度方面收到重要反馈的地方,了解推断校正实际上如何影响运行中的模拟。因此,较大的msteps通常更好。
此外,我们在source_res中定义了模拟的分辨率,并分配了名为simulator的流体求解器对象。为了创建网格,它需要访问一个Domain对象,这个对象主要是为了方便而存在:它存储了域的分辨率、物理大小和边界条件。这些信息需要传递给每个网格,因此将其以Domain的形式放在一个地方是很方便的。对于上述设置,我们需要沿x和y方向有不同的边界条件:封闭壁面和自由流进出域。
我们还在下一个单元格中实例化了实际的NN network。
# one of the most crucial parameters: how many simulation steps to look into the future while training
msteps = 4
# # this is the actual resolution in terms of cells
source_res = list(dataset.resolution)
# # this is a virtual size, in terms of abstract units for the bounding box of the domain (it's important for conversions or when rescaling to physical units)
simulation_length = 100.
# for readability
from phi.physics._boundaries import Domain, OPEN, STICKY as CLOSED
boundary_conditions = {
'y':(phi.physics._boundaries.OPEN, phi.physics._boundaries.OPEN) ,
'x':(phi.physics._boundaries.STICKY,phi.physics._boundaries.STICKY)
}
domain = phi.physics._boundaries.Domain(y=source_res[0], x=source_res[1], boundaries=boundary_conditions, bounds=Box(y=2*simulation_length, x=simulation_length))
simulator = KarmanFlow(domain=domain)
network = network_small(dict(shape=(source_res[0],source_res[1], 3)))
network.summary()
输出为:
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 64, 32, 3)] 0
conv2d (Conv2D) (None, 64, 32, 32) 2432
leaky_re_lu (LeakyReLU) (None, 64, 32, 32) 0
conv2d_1 (Conv2D) (None, 64, 32, 32) 25632
leaky_re_lu_1 (LeakyReLU) (None, 64, 32, 32) 0
conv2d_2 (Conv2D) (None, 64, 32, 32) 25632
leaky_re_lu_2 (LeakyReLU) (None, 64, 32, 32) 0
conv2d_3 (Conv2D) (None, 64, 32, 2) 1602
=================================================================
Total params: 55,298
Trainable params: 55,298
Non-trainable params: 0
_________________________________________________________________
12.6 交错模拟和神经网络
现在是整个设置中最关键的一步:我们定义一个函数,将模拟步骤和每个训练步骤中的网络评估封装起来。在定义辅助函数的所有工作之后,实际上很简单:我们通过tf.GradientTape()创建一个梯度磁带,以便稍后进行反向传播。然后,我们循环msteps,通过输入状态调用模拟器simulator.step,然后通过network(to_keras(...))评估校正。然后将NN校正添加到prediction列表中的最后一个模拟状态中(实际上我们只是用prediction[-1][1] + correction[-1]覆盖了最后一个模拟速度prediction[-1][1])。
这里发生的另一件重要的事情是归一化:网络的输入被除以dataset.dataStats中的标准差。在评估network之后,我们只剩下一个速度,因此我们只需将其乘以速度的标准差(通过* dataset.dataStats['std'][1]和[2])即可。
training_step函数还直接评估并返回损失。在这里,我们只是在整个序列上使用损失,即迭代msteps。这需要一些代码行,因为我们分别循环“x”和“y”分量,以便将其归一化并与来自训练数据集的基准真值进行比较。
“学习”发生在最后两行中,通过tape.gradient()和opt.apply_gradients(),然后包含有关如何更改NN权重以将模拟推向完整模拟步骤的参考的聚合信息。
def training_step(dens_gt, vel_gt, Re, i_step):
with tf.GradientTape() as tape:
prediction, correction = [ [dens_gt[0],vel_gt[0]] ], [0] # predicted states with correction, inferred velocity corrections
for i in range(msteps):
prediction += [
simulator.step(
density_in=prediction[-1][0],
velocity_in=prediction[-1][1],
re=Re, res=source_res[1],
)
] # prediction: [[density1, velocity1], [density2, velocity2], ...]
model_input = to_keras(prediction[-1], Re)
model_input /= math.tensor([dataset.dataStats['std'][1], dataset.dataStats['std'][2], dataset.dataStats['ext.std'][0]], channel('channels')) # [u, v, Re]
model_out = network(model_input.native(['batch', 'y', 'x', 'channels']), training=True)
model_out *= [dataset.dataStats['std'][1], dataset.dataStats['std'][2]] # [u, v]
correction += [ to_phiflow(model_out, domain) ] # [velocity_correction1, velocity_correction2, ...]
prediction[-1][1] = prediction[-1][1] + correction[-1]
# evaluate loss
loss_steps_x = [
tf.nn.l2_loss(
(
vel_gt[i].vector['x'].values.native(('batch', 'y', 'x'))
- prediction[i][1].vector['x'].values.native(('batch', 'y', 'x'))
)/dataset.dataStats['std'][1]
)
for i in range(1,msteps+1)
]
loss_steps_x_sum = tf.math.reduce_sum(loss_steps_x)
loss_steps_y = [
tf.nn.l2_loss(
(
vel_gt[i].vector['y'].values.native(('batch', 'y', 'x'))
- prediction[i][1].vector['y'].values.native(('batch', 'y', 'x'))
)/dataset.dataStats['std'][2]
)
for i in range(1,msteps+1)
]
loss_steps_y_sum = tf.math.reduce_sum(loss_steps_y)
loss = (loss_steps_x_sum + loss_steps_y_sum)/msteps
gradients = tape.gradient(loss, network.trainable_variables)
opt.apply_gradients(zip(gradients, network.trainable_variables))
return math.tensor(loss)
一旦定义了该函数,我们通过调用phiflow的math.jit_compile()函数来准备执行训练步骤。它会自动映射到所选后端的正确预编译步骤。例如,对于TF,它内部创建了一个计算图,并优化了操作链。对于JAX,它甚至可以编译优化的GPU代码(如果JAX设置正确)。因此,使用jit编译在运行时方面可以产生巨大的差异。
training_step_jit = math.jit_compile(training_step)
12.7 训练
为了训练,我们使用标准的Adam优化器,默认情况下运行5个时期。这是为了保持运行时间较短而选择的相对较低的数字。如果您有资源,进行10或15个时期将产生更准确的结果。对于更长时间的训练和更大的网络,降低学习率也将有益于时期的过程,但为了简单起见,我们将在这里保持LR为常数。
可选地,这也是加载网络状态以恢复训练的正确时机。
LR = 1e-4
EPOCHS = 5
opt = tf.keras.optimizers.Adam(learning_rate=LR)
# optional, load existing network...
# set to epoch nr. to load existing network from there
resume = 0
if resume>0:
ld_network = keras.models.load_model('./nn_epoch{:04d}.h5'.format(resume))
#ld_network = keras.models.load_model('./nn_final.h5') # or the last one
network.set_weights(ld_network.get_weights())
最终,我们可以开始训练神经网络了!现在非常简单,我们只需循环所需的迭代次数,每次通过getData获取一个批次,将其馈入源模拟输入source_in,并在损失中与批次的reference数据进行比较。
上述设置将自动处理此处使用的可微分物理求解器提供正确的梯度信息,并将其提供给tensorflow网络。请注意:由于设置的复杂性,此次训练可能需要一段时间...(如果您有来自之前运行的保存的nn_final.h5网络,您可以潜在地跳过此块并通过上面的单元格加载先前训练过的模型。)
steps = 0
for j in range(EPOCHS): # training
dataset.newEpoch(exclude_tail=msteps)
if j<resume:
print('resume: skipping {} epoch'.format(j+1))
steps += dataset.numSteps*dataset.numBatches
continue
for ib in range(dataset.numBatches):
for i in range(dataset.numSteps):
# batch: [[dens0, dens1, ...], [x-velo0, x-velo1, ...], [y-velo0, y-velo1, ...], [ReynoldsNr(s)]]
batch = getData(dataset, consecutive_frames=msteps)
dens_gt = [ # [density0:CenteredGrid, density1, ...]
domain.scalar_grid(
math.tensor(batch[0][k], math.batch('batch'), math.spatial('y, x'))
) for k in range(msteps+1)
]
vel_gt = [ # [velocity0:StaggeredGrid, velocity1, ...]
domain.staggered_grid(
math.stack(
[
math.tensor(batch[2][k], math.batch('batch'), math.spatial('y, x')),
math.tensor(batch[1][k], math.batch('batch'), math.spatial('y, x')),
], math.channel(vector="y,x")
)
) for k in range(msteps+1)
]
re_nr = math.tensor(batch[3], math.batch('batch'))
loss = training_step_jit(dens_gt, vel_gt, re_nr, math.tensor(steps))
steps += 1
if (j==0 and ib==0 and i<3) or (j==0 and ib==0 and i%128==0) or (j>0 and ib==0 and i==400): # reduce output
print('epoch {:03d}/{:03d}, batch {:03d}/{:03d}, step {:04d}/{:04d}: loss={}'.format( j+1, EPOCHS, ib+1, dataset.numBatches, i+1, dataset.numSteps, loss ))
dataset.nextStep()
dataset.nextBatch()
if j%10==9: network.save('./nn_epoch{:04d}.h5'.format(j+1))
# all done! save final version
network.save('./nn_final.h5'); print("Training done, saved NN")
运行结果:
epoch 001/005, batch 001/002, step 0001/0496: loss=2565.1914
epoch 001/005, batch 001/002, step 0002/0496: loss=1434.6736
epoch 001/005, batch 001/002, step 0003/0496: loss=724.7997
epoch 001/005, batch 001/002, step 0129/0496: loss=40.198242
epoch 001/005, batch 001/002, step 0257/0496: loss=28.450535
epoch 001/005, batch 001/002, step 0385/0496: loss=27.100056
epoch 002/005, batch 001/002, step 0401/0496: loss=8.376183
epoch 003/005, batch 001/002, step 0401/0496: loss=4.7433133
epoch 004/005, batch 001/002, step 0401/0496: loss=4.522671
epoch 005/005, batch 001/002, step 0401/0496: loss=2.0179803
Training done, saved NN
损失应该从最初的1000以上下降到10以下。这是一个好的迹象,但当然更重要的是看NN-solver组合在新输入上的表现如何。通过这种培训方法,我们实现了一个混合求解器,由一个常规的“源”模拟器和一个经过训练以与此模拟器特定交互的网络组成,适用于所选的模拟案例领域。
让我们看看将其应用于一组新雷诺数的测试数据输入时,它的表现如何。
为了使事情保持简单,我们不会追求高性能版本的混合求解器。有关性能,请查看外部代码库:这里训练的网络应该直接可用于此应用脚本中。
12.8 评估
为了评估我们基于深度学习的求解器的性能,我们基本上只需要在每个训练迭代的内部循环中重复更多步骤。虽然在训练时我们受限于 msteps 次评估,但现在我们可以运行我们的求解器以任意长度。这是一个很好的测试,用于检验我们的求解器学习如何将数据保持在所需的分布中,并代表了更长回放的泛化测试。
我们重复使用上面的求解器代码,但在接下来,我们将考虑两个模拟版本:为了比较,我们将在“源”空间(即没有任何修改)中运行一个参考模拟。这个版本接收模拟器每次评估的常规输出,并忽略学习到的校正(存储在下面的 steps_source 中)。第二个版本是重复计算源求解器加上学习到的校正,并在求解器中推进这个状态(steps_hybrid)。
我们还需要一组新数据。下面,我们将下载一组新的雷诺数(在用于训练的雷诺数之间),在这些雷诺数上我们将运行未修改的模拟器和基于深度学习的模拟器。
fname_test = 'sol-karman-2d-test.pickle'
if not os.path.isfile(fname_test):
print("Downloading test data (38MB), this can take a moment the first time...")
urllib.request.urlretrieve("https://physicsbaseddeeplearning.org/data/"+fname_test, fname_test)
with open(fname_test, 'rb') as f: data_test_preloaded = pickle.load(f)
print("Loaded test data, {} training sims".format(len(data_test_preloaded)) )
输出:
Downloading test data (38MB), this can take a moment the first time...
Loaded test data, 4 training sims
接下来,我们创建一个新的数据集对象dataset_test,以组织数据。我们只是使用未打乱的数据集的第一个批次。
然而,有一个微妙但重要的问题:我们仍然必须使用原始训练数据集的标准化:dataset.dataStats['std']值。测试数据集有它自己的均值和标准差,因此训练过的神经网络从未见过这些数据。神经网络是使用上面的dataset中的数据进行训练的,因此我们必须使用那里的常量进行标准化,以确保网络接收到能够与其训练的数据相关的值。
dataset_test = Dataset( data_preloaded=data_test_preloaded, is_testset=True, num_frames=simsteps, num_sims=4, batch_size=4 )
# we only need 1 batch with t=0 states to initialize the test simulations with
dataset_test.newEpoch(shuffle_data=False)
batch = getData(dataset_test, consecutive_frames=0)
re_nr_test = math.tensor(batch[3], math.batch('batch')) # Reynolds numbers
print("Reynolds numbers in test data set: "+format(re_nr_test))
输出:
Reynolds numbers in test data set: (120000.000, 480000.000, 1920000.000, 7680000.000) along batch
接下来,我们构建一个math.tensor作为居中标记场的初始状态,并从测试集批次的下两个索引中构建一个交错网格。类似于上面的to_phiflow,我们使用phi.math.stack()将适当大小的两个场组合成一个交错网格。
source_dens_initial = math.tensor( batch[0][0], math.batch('batch'), math.spatial('y, x'))
source_vel_initial = domain.staggered_grid(phi.math.stack([
math.tensor(batch[2][0], math.batch('batch'),math.spatial('y, x')),
math.tensor(batch[1][0], math.batch('batch'),math.spatial('y, x'))], channel(vector="y,x")) )
现在我们首先为基准运行 120 步的源模拟:
source_dens_test, source_vel_test = source_dens_initial, source_vel_initial
steps_source = [[source_dens_test,source_vel_test]]
STEPS=100
# note - math.jit_compile() not useful for numpy solve... hence not necessary here
for i in range(STEPS):
[source_dens_test,source_vel_test] = simulator.step(
density_in=source_dens_test,
velocity_in=source_vel_test,
re=re_nr_test,
res=source_res[1],
)
steps_source.append( [source_dens_test,source_vel_test] )
print("Source simulation steps "+format(len(steps_source)))
结果:
Source simulation steps 101
接下来,我们计算我们学习到的混合求解器的相应状态。在这里,我们紧密地遵循训练代码,但是现在没有任何梯度磁带或损失计算。我们仅对每个模拟状态进行前向传递来评估神经网络,以计算校正场:
source_dens_test, source_vel_test = source_dens_initial, source_vel_initial
steps_hybrid = [[source_dens_test,source_vel_test]]
for i in range(STEPS):
[source_dens_test,source_vel_test] = simulator.step(
density_in=source_dens_test,
velocity_in=source_vel_test,
re=math.tensor(re_nr_test),
res=source_res[1],
)
model_input = to_keras([source_dens_test,source_vel_test], re_nr_test )
model_input /= math.tensor([dataset.dataStats['std'][1], dataset.dataStats['std'][2], dataset.dataStats['ext.std'][0]], channel('channels')) # [u, v, Re]
model_out = network(model_input.native(['batch', 'y', 'x', 'channels']), training=False)
model_out *= [dataset.dataStats['std'][1], dataset.dataStats['std'][2]] # [u, v]
correction = to_phiflow(model_out, domain)
source_vel_test = source_vel_test + correction
steps_hybrid.append( [source_dens_test, source_vel_test] )
print("Steps with hybrid solver "+format(len(steps_hybrid)))
Steps with hybrid solver 101
根据存储的状态,我们量化神经网络带来的改进,并可视化结果。在下面的单元格中,索引b选择四个测试模拟中的一个(默认为索引0,低于训练数据范围之外的最低Re),并计算所有时间步长上的累积平均绝对误差(MAE)。
import pylab
b = 0 # batch index for the following comparisons
errors_source, errors_pred = [], []
for index in range(STEPS):
vx_ref = dataset_test.dataPreloaded[ dataset_test.dataSims[b] ][ index ][1][0,...]
vy_ref = dataset_test.dataPreloaded[ dataset_test.dataSims[b] ][ index ][2][0,...]
vxs = vx_ref - steps_source[index][1].values.vector[1].numpy('batch,y,x')[b,...]
vxh = vx_ref - steps_hybrid[index][1].values.vector[1].numpy('batch,y,x')[b,...]
vys = vy_ref - steps_source[index][1].values.vector[0].numpy('batch,y,x')[b,...]
vyh = vy_ref - steps_hybrid[index][1].values.vector[0].numpy('batch,y,x')[b,...]
errors_source.append(np.mean(np.abs(vxs)) + np.mean(np.abs(vys)))
errors_pred.append(np.mean(np.abs(vxh)) + np.mean(np.abs(vyh)))
fig = pylab.figure().gca()
pltx = np.linspace(0,STEPS-1,STEPS)
fig.plot(pltx, errors_source, lw=2, color='mediumblue', label='Source')
fig.plot(pltx, errors_pred, lw=2, color='green', label='Hybrid')
pylab.xlabel('Time step'); pylab.ylabel('Error'); fig.legend()
print("MAE for source: "+format(np.mean(errors_source)) +" , and hybrid: "+format(np.mean(errors_pred)) )
输出结果:
MAE for source: 0.12054027616977692 , and hybrid: 0.04435234144330025
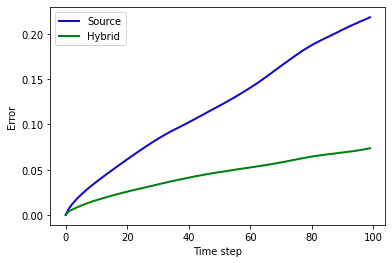
由于训练的复杂性, 性能各不相同, 但通常常规模拟的整体 MAE 约为混合模拟器的 2.5 倍。上图也显示了这种随时间的行为。通常甚至对于训练数据范围内的其他雷诺数,差距更大 (对上面的 b 尝试其他值)。
我们还通过绘制速度 y 分量随时间可视化两个输出的差异。以下两个代码单元显示了批处理索引 b 的六个速度快照, 以 20 个时间步长的间隔。
c = 0 # channel selector, x=1 or y=0
interval = 20 # time interval
IMGS = STEPS//20+1
fig, axes = pylab.subplots(1, IMGS, figsize=(16, 5))
for i in range(0,IMGS):
v = steps_source[i*interval][1].values.vector[c].numpy('batch,y,x')[b,...]
axes[i].imshow( v , origin='lower', cmap='magma')
axes[i].set_title(f" Source simulation t={i*interval} ")
pylab.tight_layout()
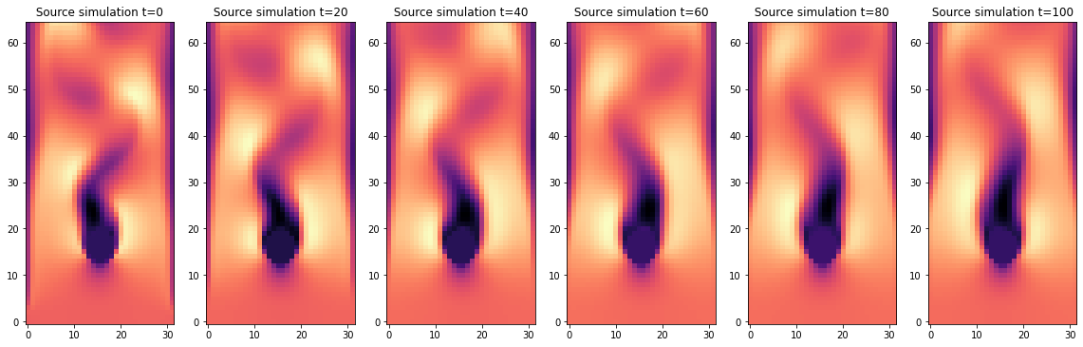
fig, axes = pylab.subplots(1, IMGS, figsize=(16, 5))
for i in range(0,IMGS):
v = steps_hybrid[i*interval][1].values.vector[c].numpy('batch,y,x')[b,...]
axes[i].imshow( v , origin='lower', cmap='magma')
axes[i].set_title(f" Hybrid solver t={i*interval} ")
pylab.tight_layout()
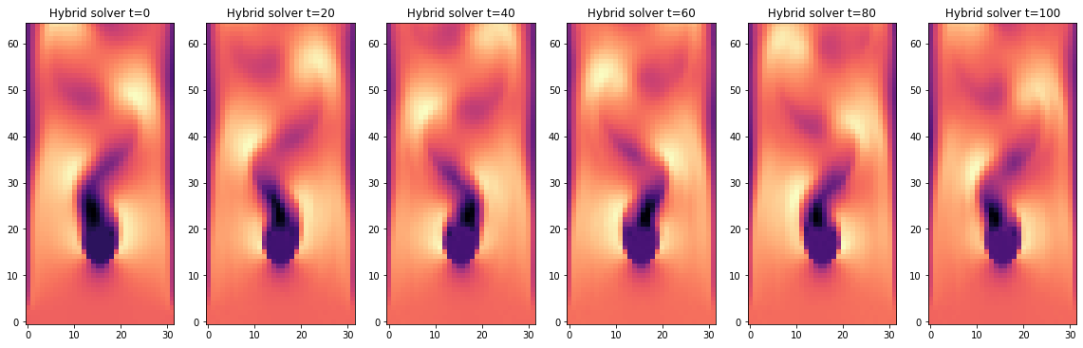
它们在时都以相同的初始状态开始(参考解流形的下采样解),在时,两个解仍然具有相似性。随着时间的推移,源版本强烈扩散了流动中的结构并失去了动量。障碍物后面的流动变得笔直,缺乏明显的涡旋。
混合求解器生成的版本要好得多。即使经过一百多次更新,它仍然保留了涡 shedding。请注意,这两个输出都是由相同的基础求解器生成的。第二个版本仅仅受益于学习到的修正器,它成功地恢复了源求解器的数值误差,包括其过度强的耗散。
我们还通过视觉比较NN相对于参考数据的表现。下一个单元格绘制了三个版本的一个时间步长:经过50步的参考数据,以及源和我们的混合求解器的重新模拟版本,以及两者的每个单元格误差。
index = STEPS//2 # time step index
vx_ref = dataset_test.dataPreloaded[ dataset_test.dataSims[b] ][ index ][1][0,...]
vx_src = steps_source[index][1].values.vector[1].numpy('batch,y,x')[b,...]
vx_hyb = steps_hybrid[index][1].values.vector[1].numpy('batch,y,x')[b,...]
fig, axes = pylab.subplots(1, 4, figsize=(14, 5))
axes[0].imshow( vx_ref , origin='lower', cmap='magma')
axes[0].set_title(f" Reference ")
axes[1].imshow( vx_src , origin='lower', cmap='magma')
axes[1].set_title(f" Source ")
axes[2].imshow( vx_hyb , origin='lower', cmap='magma')
axes[2].set_title(f" Learned ")
# show error side by side
err_source = vx_ref - vx_src
err_hybrid = vx_ref - vx_hyb
v = np.concatenate([err_source,err_hybrid], axis=1)
axes[3].imshow( v , origin='lower', cmap='cividis')
axes[3].set_title(f" Errors: Source & Learned")
pylab.tight_layout()
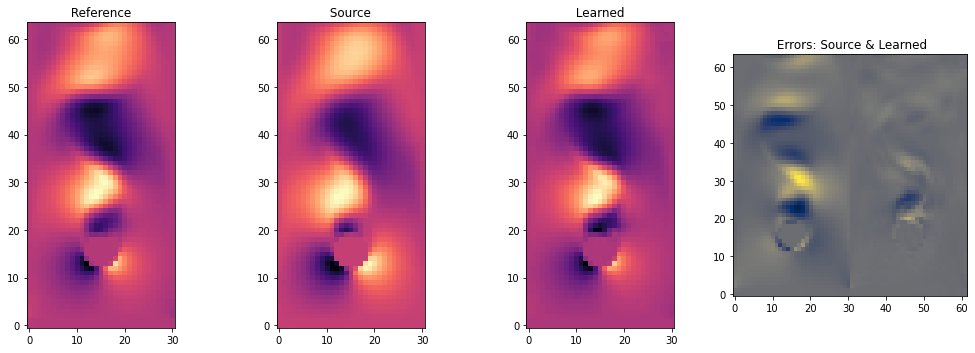
这清晰地展示了中间的纯源模拟与左侧参考解的偏差。学习版本与参考解的接近程度更高。
右侧的两个每单元误差图像也说明了这一点:源版本具有更大的误差(即更亮的颜色),显示它系统地低估了应该形成的涡旋。学习版本的误差分布更加均匀,且数量级显著较小。
本次评估到此结束。需要注意的是,混合求解器的改进行为往往难以通过简单的向量范数(如MAE或范数)进行可靠的测量。为了改进这一点,我们需要采用其他特定领域的指标。在本例中,基于流动涡度和湍流特性的流体度量将是适用的。然而,在本文中,我们希望集中讨论与DL相关的主题,并在下一章中针对另一个可微物理求解器的反问题进行研究。
12.9 下一步
-
修改训练以进一步减少训练误差。使用中等规模的网络, 您应该能将损失降低到约 1。
-
关闭可微分物理训练 (通过设置
msteps=1), 并与 DP 版本进行比较。 -
类似地, 用更大的
msteps设置训练网络, 例如 8 或 16。请注意, 由于训练的递归性质, 您可能需要加载预训练状态来稳定最初的迭代。 -
使用外部 github 代码生成新的测试数据, 并在这些用例上运行您的训练好的神经网络。您会发现, 降低训练误差不总是直接相关于改进的测试性能。
逆问题包含了科学中的大量实际应用。一般来说,这里的目标不是直接计算一个物理场,如未来某个时间的速度(这是正解的典型情况),而是更通用地计算模型方程中的一个或多个参数,从而满足某些约束条件。一个非常常见的目标是在某些约束条件下找到单个参数的最优设置。例如,这可能是一个平流扩散模型的全局扩散常数,使其尽可能精确地符合测量数据。通过观测或重建初始条件(如粒子成像测速)来调整任何模型参数,都会遇到逆问题。更复杂的情况旨在计算最佳条件下的边界几何形状,例如在流体流动中获得阻力最小的形状。
下面的一个关键方面是,我们的目标并不只是求解一个逆问题的_单个实例,而是希望使用深度学习来解决更多的逆问题。因此,与{doc}physicalloss-code或{doc}diffphys-code-ns的可微分物理(DP)优化不同,我们已经解决了逆问题特定实例的优化问题,而我们现在的目标是训练一个学习求解更大类逆问题(即整个求解流形)的 NN。不过,我们当然需要依赖这些问题在一定程度上的相似性,否则就没有什么可学的了(解流形中隐含的连续性假设也就不成立了)。
下面我们将运行一个极具挑战性的测试案例,作为这些逆问题的代表:我们的目标是计算一个高维控制函数,在不可压缩流体模拟的整个过程中施加力,以达到流体中被动迁移标记的预期目标状态。这意味着我们只有非常间接的约束条件需要满足(序列结束时的单一状态)和大量自由度(控制力函数是一个时空函数,其自由度与流场本身相同)。
控制的长期性是这是一个棘手的逆问题的原因之一:物理系统状态的任何变化都可能导致后期的巨大变化,因此控制器需要预测系统在受到影响时的行为。这意味着网络还需要学习底层物理是如何演变和变化的,而这正是 DP 训练中的梯度发挥作用的地方,它可以引导学习任务朝着能够实现目标解的方向前进。
13.1 描述
使用overview-equations 中的符号,可以得到最小化问题
其中, 表示标记场目标状态的样本, 表示标记密度的模拟状态。与之前一样,索引 表示在不同空间位置(通常是所有网格单元)对我们的解进行采样,而索引 则表示大量不同目标状态的集合。
我们的目标是训练两个权重分别为 和 的网络,从而使序列:
使上述损失最小。网络是一个预测器,它确定了的行动应该瞄准的状态,也就是说,其进行长期规划并据此确定了操作。给定目标 ,它计算 。 通过计算 以可加方式作用于速度场,其中我们使用 和 分别表示 和 的神经网络表示,使用表示目标密度状态。和 表示相应的网络权重。
对于这个问题,模型偏微分方程 包含速度为 的二维不可压缩纳维-斯托克斯方程的离散化版本:
没有显式粘度,标记密度 的额外传输方程为 。
总结一下, 我们有一个预测器 ,其给出一个方向, 一个行为体 对物理模型 施加力。它们都需要配合才能在 次模拟迭代后达到给定的目标。从这个公式可以看出, 这并不是一个简单的逆问题,尤其是因为所有三个函数都是非线性的。这正是 DP 方法的梯度如此重要的原因。(上述观点还表明强化学习是一种潜在的选择。在{doc} reinflearn-code 中, 我们将比较 DP 与这些替代方法。)
13.2 不可压缩流体的控制
接下来的章节将引导您使用 ΦFlow完成从数据生成到网络训练的所有必要步骤。由于控制问题的复杂性,我们将先对网络进行有监督的初始化,然后再使用 DP 进行更精确的端到端训练。(注意:本例使用的是ΦFlow的旧版本 1.4.1)
下面的代码复制了Learning to Control PDEs with Differentiable Physics{cite}"holl2019pdecontrol "中的一个反问题示例(形状转换实验),更多细节可参见论文附录的 D.2 节。
首先,我们需要加载 phiflow 并查看 PDE-Control的 git 仓库,其中还包含一些带有初始形状的 numpy 数组。
!pip install --quiet phiflow==1.4.1
import matplotlib.pyplot as plt
from phi.flow import *
if not os.path.isdir('PDE-Control'):
print("Cloning, PDE-Control repo, this can take a moment")
os.system("git clone --recursive https://github.com/holl-/PDE-Control.git")
# now we can load the necessary phiflow libraries and helper functions
import sys; sys.path.append('PDE-Control/src')
from shape_utils import load_shapes, distribute_random_shape
from control.pde.incompressible_flow import IncompressibleFluidPDE
from control.control_training import ControlTraining
from control.sequences import StaggeredSequence, RefinedSequence
13.3 数据生成
在开始训练之前,我们必须生成一个训练数据集,即一组真值时间序列 。由于下面的训练非常复杂,我们将采用一种分阶段的方法,先预先训练一个有监督的网络作为粗略的初始化,然后再对其进行改进,使其能够学习控制,并将目光越放越远。(这将通过训练处理越来越长序列的专门网络来实现)。
首先,让我们设置一个域和数据生成步骤的基本参数。
domain = Domain([64, 64]) # 1D Grid resolution and physical size
step_count = 16 # how many solver steps to perform
dt = 1.0 # Time increment per solver step
example_count = 1000
batch_size = 100
data_path = 'shape-transitions'
pretrain_data_path = 'moving-squares'
shape_library = load_shapes('PDE-Control/notebooks/shapes')
最后一行中的 shape_library 包含十种不同的形状,我们将使用它们在随机位置初始化标记密度。
这就是这些形状的样子:
import pylab
pylab.subplots(1, len(shape_library), figsize=(17, 5))
for t in range(len(shape_library)):
pylab.subplot(1, len(shape_library), t+1)
pylab.imshow(shape_library[t], origin='lower')

下面的单元格使用这些形状来创建我们要训练网络的数据集。每个示例都由起始帧和目标帧(结束帧)组成,起始帧和目标帧是通过在域内某处放置shape_library中的随机形状生成的。
for scene in Scene.list(data_path): scene.remove()
for _ in range(example_count // batch_size):
scene = Scene.create(data_path, count=batch_size, copy_calling_script=False)
print(scene)
start = distribute_random_shape(domain.resolution, batch_size, shape_library)
end__ = distribute_random_shape(domain.resolution, batch_size, shape_library)
[scene.write_sim_frame([start], ['density'], frame=f) for f in range(step_count)]
scene.write_sim_frame([end__], ['density'], frame=step_count)
shape-transitions/sim_000000
shape-transitions/sim_000100
shape-transitions/sim_000200
shape-transitions/sim_000300
shape-transitions/sim_000400
shape-transitions/sim_000500
shape-transitions/sim_000600
shape-transitions/sim_000700
shape-transitions/sim_000800
shape-transitions/sim_000900
由于该数据集不包含任何中间帧,因此无法进行监督预训练。这是因为预训练 CFE 网络需要两个连续帧,而预训练 网络则需要三个距离为 的帧。
相反,我们创建了包含这些中间帧的第二个数据集。这个数据集不需要与实际数据集非常接近,因为它只用于通过预训练进行网络初始化。在这里,我们围绕域线性移动一个矩形。
for scene in Scene.list(pretrain_data_path): scene.remove()
for scene_index in range(example_count // batch_size):
scene = Scene.create(pretrain_data_path, count=batch_size, copy_calling_script=False)
print(scene)
pos0 = np.random.randint(10, 56, (batch_size, 2)) # start position
pose = np.random.randint(10, 56, (batch_size, 2)) # end position
size = np.random.randint(6, 10, (batch_size, 2))
for frame in range(step_count+1):
time = frame / float(step_count + 1)
pos = np.round(pos0 * (1 - time) + pose * time).astype(np.int)
density = AABox(lower=pos-size//2, upper=pos-size//2+size).value_at(domain.center_points())
scene.write_sim_frame([density], ['density'], frame=frame)
moving-squares/sim_000000
moving-squares/sim_000100
moving-squares/sim_000200
moving-squares/sim_000300
moving-squares/sim_000400
moving-squares/sim_000500
moving-squares/sim_000600
moving-squares/sim_000700
moving-squares/sim_000800
moving-squares/sim_000900
13.4 监督初始化
首先,我们将 1000 个数据样本分成 100 个测试样本、100 个验证样本和 800 个训练样本。
test_range = range(100)
val_range = range(100, 200)
train_range = range(200, 1000)
下面的单元训练所有 .这里的 表示网络预测目标的时间步数。为了覆盖更长的时间跨度,我们在这里使用系数 2 来分层划分物理系统应受控制的时间间隔。
ControlTraining 类用于设置相应的优化问题。监督初始化的损失定义为中心帧处的速度观测损失:
因此,不需要模拟序列(sequence_class=None),只需要在帧 处进行观测损失(obs_loss_frames=[n // 2])。预训练的网络检查点存储在 supervised_checkpoints 中。
注:下一个单元将运行一段时间。PDE-Control git 仓库附带了一组预训练网络。因此,如果您想专注于评估,可以跳过训练,直接加载预训练网络,方法是注释掉训练单元格,并取消注释加载下面的单元格。
supervised_checkpoints = {}
for n in [2, 4, 8, 16]:
app = ControlTraining(n, IncompressibleFluidPDE(domain, dt),
datapath=pretrain_data_path, val_range=val_range, train_range=train_range, trace_to_channel=lambda _: 'density',
obs_loss_frames=[n//2], trainable_networks=['OP%d' % n],
sequence_class=None).prepare()
for i in range(1000):
app.progress() # Run Optimization for one batch
supervised_checkpoints['OP%d' % n] = app.save_model()
supervised_checkpoints # this is where the checkpoints end up when re-training:
{'OP16': '/root/phi/model/control-training/sim_000003/checkpoint_00001000',
'OP2': '/root/phi/model/control-training/sim_000000/checkpoint_00001000',
'OP4': '/root/phi/model/control-training/sim_000001/checkpoint_00001000',
'OP8': '/root/phi/model/control-training/sim_000002/checkpoint_00001000'}
# supervised_checkpoints = {'OP%d' % n: 'PDE-Control/networks/shapes/supervised/OP%d_1000' % n for n in [2, 4, 8, 16]}
至此,OP 网络的预训练结束。通过这些网络,我们至少可以对运动进行粗略规划,并在接下来的端到端训练中加以完善。不过,在此之前,我们将对 网络进行初始化,这样我们就可以执行操作,即对模拟施加力。这与 网络是完全分离的。
13.5 使用可微分物理的 CFE 预训练
为了对 网络进行预训练,我们使用可微分求解器进行了一次模拟。
下面的单元格将从头开始训练 网络。如果你手头有一个预训练的网络,可以跳过训练,通过运行之后的单元来加载检查点。
app = ControlTraining(1, IncompressibleFluidPDE(domain, dt),
datapath=pretrain_data_path, val_range=val_range, train_range=train_range, trace_to_channel=lambda _: 'density',
obs_loss_frames=[1], trainable_networks=['CFE']).prepare()
for i in range(1000):
app.progress() # Run Optimization for one batch
supervised_checkpoints['CFE'] = app.save_model()
# supervised_checkpoints['CFE'] = 'PDE-Control/networks/shapes/CFE/CFE_2000'
请注意,由于 网络只推断状态对之间的作用力,因此我们实际上并没有设置模拟训练。
# [TODO, show preview of CFE only?]
13.6 使用可微分物理的端到端训练
现在,两种网络类型的第一个版本都已存在,我们可以启动当前设置中最重要的步骤:通过可微分流体求解器对两种网络进行端到端耦合训练。虽然预训练阶段依赖于监督训练,但下一步将显著提高控制质量。
为了在 phiflow 中使用可微分物理损失对 和所有 网络进行端到端训练,我们使用交错执行方案创建了一个新的 ControlTraining"实例。
下面的单元格在不初始化网络权重的情况下,用 step_count 求解器步骤构建计算图。
staggered_app = ControlTraining(step_count, IncompressibleFluidPDE(domain, dt),
datapath=data_path, val_range=val_range, train_range=train_range, trace_to_channel=lambda _: 'density',
obs_loss_frames=[step_count], trainable_networks=['CFE', 'OP2', 'OP4', 'OP8', 'OP16'],
sequence_class=StaggeredSequence, learning_rate=5e-4).prepare()
App created. Scene directory is /root/phi/model/control-training/sim_000005 (INFO), 2021-04-09 00:41:17,299n
Sequence class: <class 'control.sequences.StaggeredSequence'> (INFO), 2021-04-09 00:41:17,305n
Partition length 16 sequence (from 0 to 16) at frame 8
Partition length 8 sequence (from 0 to 8) at frame 4
Partition length 4 sequence (from 0 to 4) at frame 2
Partition length 2 sequence (from 0 to 2) at frame 1
Execute -> 1
Execute -> 2
Partition length 2 sequence (from 2 to 4) at frame 3
Execute -> 3
Execute -> 4
Partition length 4 sequence (from 4 to 8) at frame 6
Partition length 2 sequence (from 4 to 6) at frame 5
Execute -> 5
Execute -> 6
Partition length 2 sequence (from 6 to 8) at frame 7
Execute -> 7
Execute -> 8
Partition length 8 sequence (from 8 to 16) at frame 12
Partition length 4 sequence (from 8 to 12) at frame 10
Partition length 2 sequence (from 8 to 10) at frame 9
Execute -> 9
Execute -> 10
Partition length 2 sequence (from 10 to 12) at frame 11
Execute -> 11
Execute -> 12
Partition length 4 sequence (from 12 to 16) at frame 14
Partition length 2 sequence (from 12 to 14) at frame 13
Execute -> 13
Execute -> 14
Partition length 2 sequence (from 14 to 16) at frame 15
Execute -> 15
Execute -> 16
Target loss: Tensor("truediv_16:0", shape=(), dtype=float32) (INFO), 2021-04-09 00:41:44,654n
Force loss: Tensor("truediv_107:0", shape=(), dtype=float32) (INFO), 2021-04-09 00:41:51,312n
Supervised loss at frame 16: Tensor("truediv_108:0", shape=(), dtype=float32) (INFO), 2021-04-09 00:41:51,332n
Setting up loss (INFO), 2021-04-09 00:41:51,338n
Preparing data (INFO), 2021-04-09 00:42:32,417n
Initializing variables (INFO), 2021-04-09 00:42:32,443n
Model variables contain 0 total parameters. (INFO), 2021-04-09 00:42:36,418n
Validation (000000): Learning_Rate: 0.0005, GT_obs_16: 399498.75, Loss_reg_unscaled: 1.2424506, Loss_reg_scale: 1.0, Loss: 798997.5 (INFO), 2021-04-09 00:42:59,618n
接下来的单元格使用监督检查点初始化网络, 然后联合训练所有网络。您可以增加优化步骤的数量或多次执行下一个单元格以进一步提高性能。
注意: 下一单元格需要运行一段时间。或者, 您可以跳过此单元格, 改为使用下面单元格中的代码加载预训练网络。
staggered_app.load_checkpoints(supervised_checkpoints)
for i in range(1000):
staggered_app.progress() # run staggered Optimization for one batch
staggered_checkpoint = staggered_app.save_model()
# staggered_checkpoint = {net: 'PDE-Control/networks/shapes/staggered/all_53750' for net in ['CFE', 'OP2', 'OP4', 'OP8', 'OP16']}
# staggered_app.load_checkpoints(staggered_checkpoint)
既然网络已经训练好了,我们就可以从测试集中推断出一些轨迹。(这与原论文中的图 5b 和 18b 相对应)
下面的单元格选取了前 100 个配置,即 "test_range "定义的测试集,并让网络推断出相应逆问题的解。
states = staggered_app.infer_all_frames(test_range)
通过下面的索引列表 "批次",您可以选择显示部分解决方案。每一行显示的都是一个时间序列,从初始条件开始,在 16 个时间步长内使用 NN 控制力进行模拟演化。最后一步,即 应该与最右边图片中显示的目标一致。
batches = [0,1,2]
pylab.subplots(len(batches), 10, sharey='row', sharex='col', figsize=(14, 6))
pylab.tight_layout(w_pad=0)
# solutions
for i, batch in enumerate(batches):
for t in range(9):
pylab.subplot(len(batches), 10, t + 1 + i * 10)
pylab.title('t=%d' % (t * 2))
pylab.imshow(states[t * 2].density.data[batch, ..., 0], origin='lower')
# add targets
testset = BatchReader(Dataset.load(staggered_app.data_path,test_range), staggered_app._channel_struct)[test_range]
for i, batch in enumerate(batches):
pylab.subplot(len(batches), 10, i * 10 + 10)
pylab.title('target')
pylab.imshow(testset[1][i,...,0], origin='lower')
正如您在最右边的两列中看到的,该网络在求解这些逆问题方面做得非常出色:流体标记被推到正确的位置,并以正确的方式变形以匹配目标。
对神经网络来说,这里看起来相当简单的事情实际上是一项棘手的任务:它需要在 16 个时间积分步长内指导完整的二维纳维-斯托克斯模拟。因此,如果施加的力稍有偏差或不连贯,流体就会开始混乱地旋转和运动。不过,网络已经学会了保持运动的一致性,并引导标记密度到达目标位置。
接下来,我们通过比较最终密度配置相对于初始密度的平均绝对误差来量化误差率。按照上述标准训练设置,下一个单元的相对残余误差应为 5-6%。反之亦然,这意味着约 94% 以上的标记密度最终会出现在正确的位置上!
errors = []
for batch in enumerate(test_range):
initial = np.mean( np.abs( states[0].density.data[batch, ..., 0] - testset[1][batch,...,0] ))
solution = np.mean( np.abs( states[16].density.data[batch, ..., 0] - testset[1][batch,...,0] ))
errors.append( solution/initial )
print("Relative MAE: "+format(np.mean(errors)))
Relative MAE: 0.05450168251991272
13.7 下一步
要对此源代码进行进一步实验, 您可以例如:
- 更改
test_range索引以查看不同的示例, 或使用新的形状作为目标来测试训练控制器网络的概括能力。 - 尝试使用
RefinedSequence(而不是StaggeredSequence)与预测细化方案一起进行训练。这将进一步改善控制并减少密度误差。
前面的章节已经解释了可微分物理学方法在深度学习中的应用,并给出了一系列例子:从基本的梯度计算到由高级模拟驱动的复杂学习设置。现在是时候退后一步进行评估了:最终,这些方法中的可微分物理学组件并不太复杂。它们主要基于现有的数值方法,重点是有效地利用这些方法不仅进行前向模拟,还要计算梯度信息。在这种情况下,主要令人兴奋的是这些数值方法与深度学习相结合所带来的影响。

14.1 集成
最重要的是,通过可微分物理训练,我们能够无缝地将这两个领域结合起来:我们可以获得混合方法,使用我们可以使用的最佳数值方法进行模拟本身以及训练过程。然后,我们可以使用训练好的模型来改进正向或反向求解。因此,最终我们拥有一个求解器,结合了传统求解器和学习组件,在组合中可以提高数值方法的能力。
14.2 交互
一个关键的方面是让神经网络在训练时与偏微分方程求解器进行交互,这对于这些混合模型的良好运行非常重要。可微分模拟允许训练模型“探索和体验”物理环境,并在求解器迭代过程中接收有针对性的反馈。这种组合很好地适应了可微分编程作为机器学习中更广泛背景的情况。
14.3 泛化
混合方法对于模拟器也具有特别的潜力:它通过让 PDE 求解器处理数据分布的大规模变化,从而提高训练模型的泛化能力,使得学习的模型可以专注于离散化未能捕捉的局部结构。虽然物理模型的泛化能力非常好,但学习模型通常专门针对训练时看到的数据分布。例如,对于上一章减少数值误差的模型,已经证明训练的模型可以处理具有大量不同物理行为的解流形,而简单的训练变体很快在重复时间步骤的过程中恶化。

总结一下, 通过 DP 训练神经网络的优缺点:
✅ 优点:
- 使用物理模型和数值方法进行离散化。
- 所选方法的效率和准确性转移到训练中。
- 物理模型和神经网络可以非常紧密地耦合。
- 通过求解器交互改进泛化。
❌ 缺点:
- 不能兼容所有的模拟器 (需要提供梯度)。
- 需要比前面讨论的方法更多的重型机器 (在框架支持方面)。
展望:随着深度学习领域中软件和 API 的发展速度,关于重型机械的最后一个负面点必将得到极大的改善。然而,目前重要的是要记住,并非每个模拟器都适合直接用于 DP 训练。因此,在本书中,我们将重点关注使用 phiflow 的示例,该软件旨在与深度学习框架进行接口设计。
通过可微物理训练(DP),我们能够将完整的数值模拟集成到深度神经网络的训练中。这也是一种非常通用的方法,适用于各种基于 PDE 模型和深度学习的组合。
在接下来的章节中,我们将首先将 DP 训练与控制问题的无模型替代方案进行比较,然后针对底层学习过程进行目标定位,以获得更好的神经网络状态。
深度强化学习,简称强化学习(RL),是深度学习领域中的一类方法,它使得人工智能代理能够探索与周围环境的交互。在此过程中,代理接收其行为的奖励信号,并尝试确定哪些行为有助于获得更高的奖励,以相应地调整其行为。RL已经在玩围棋等游戏方面取得了很大成功{cite}silver2017mastering,并为机器人等工程应用带来了希望。
强化学习的设置通常由两部分组成:环境和代理。环境接收代理的动作,同时以状态和奖励的形式提供观察结果。观察结果表示代理能够感知的环境状态信息的一部分。奖励由预定义的函数给出,通常是针对环境进行定制的,并可能包含游戏得分、错误动作的惩罚或成功完成任务的奖励等内容。
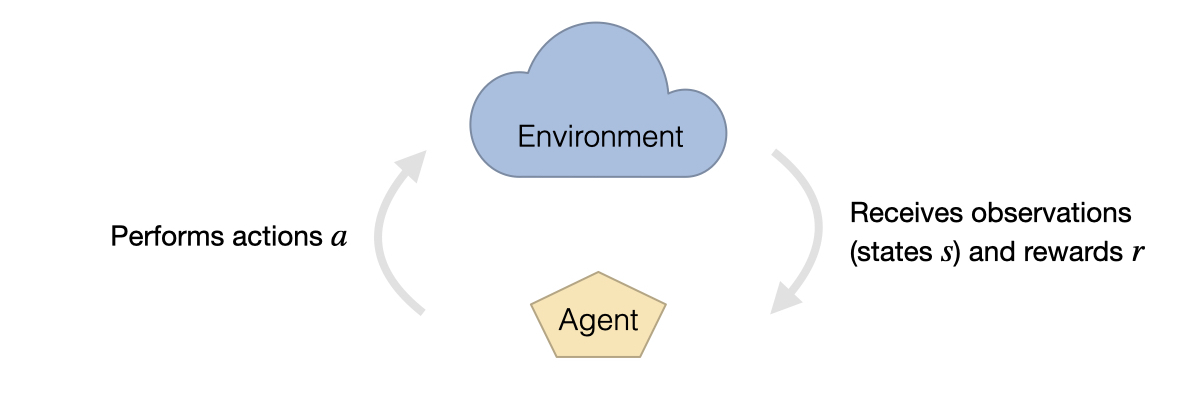
简单来说, 强化学习任务的学习目标可以表示为:
在这里,时刻的奖励(上面表示为)是由代理执行的动作的结果。代理根据神经网络策略选择它们的动作,这个策略通过一组给定的观察结果来决定。策略返回动作的概率,并且是基于环境状态和权重的条件概率。
在学习过程中,强化学习的中心目标是利用状态、动作和相应的奖励的综合信息,增加每条轨迹上奖励信号的累积强度。为了实现这个目标,提出了多种算法,可以大致分为两类:策略梯度和基于价值的方法(参见[Sutton and Barto, 2018])。
15.1 算法
在普通的策略梯度方法中,训练好的神经网络直接从环境观测中选择动作。在学习过程中,神经网络被训练用于推断动作的概率。在这里,导致剩余轨迹中获得更高回报的动作的概率会增加,而回报较小的动作则会变得不太可能。
另一方面,基于价值的方法,如_Q-Learning_,通过优化状态-动作值函数,即所谓的_Q函数_来工作。在这种情况下,网络接收状态和动作,以预测从该输入产生的剩余轨迹的平均累积奖励,即。然后根据状态选择最大化的动作。
此外,_演员-评论家_方法结合了两种方法的元素。在这里,策略网络生成的动作会根据相应状态潜力的变化进行评估。这些值由另一个神经网络给出,并近似于给定状态的预期累积奖励。近端策略优化(Proximal policy optimization,PPO){cite}schulman2017proximal是这类算法中的一个例子,也是本章示例任务(将Burgers方程作为物理环境进行控制)的选择。

15.2 近端策略优化
由于PPO方法是一种演员-评论家方法,我们需要训练两个相互依赖的网络:演员和评论家。
演员的目标本质上依赖于评论家网络的输出(它提供了哪些行动值得执行的反馈),反之评论家依赖于演员网络生成的行动(这决定了要探索哪些状态)。
这种相互依赖关系可能会促进不稳定性,例如,强烈的过度或低估的状态值可能会在学习过程中给出错误的冲动。产生更高奖励的行动通常也有助于达到具有更高信息价值的状态。因此,当允许个别样本的可能不正确的价值估计无限制地影响代理的行为时,学习进展可能会崩溃。
PPO被引入作为一种特别对抗这个问题的方法。其想法是限制个别状态价值估计对演员行为变化在学习过程中的影响。PPO在处理连续行动空间时是一个流行的选择。这可以归因于它倾向于实现良好的结果和稳定的学习进展,同时仍然相对容易实现。
15.2.1 PPO-clip
更具体地说,我们将使用算法_PPO-clip_ {cite}“schulman2017proximal”。这种PPO变体为由单个更新步骤引起的行为变化设置了硬限制。因此,该算法使用先前的网络状态(在下面用下标表示)来限制学习过程中每步的变化。在接下来的内容中,我们将把演员网络的网络参数表示为,批评家的网络参数表示为。
15.2.2 Actor
该演员计算一个策略函数,返回在当前网络参数和状态条件下行动的概率分布。
在接下来的内容中,我们将用表示从分布中选择特定动作的概率。如上所述,训练过程使用固定的先前网络状态进行策略评估,计算一定数量的权重更新,并在间隔中重新初始化先前的权重为。为了限制变化,目标函数使用函数,简单地返回被夹在区间内。
定义了与先前策略的偏差界限。结合起来,演员的目标函数由以下表达式给出:
由于演员网络被训练为提供期望值,在训练时会使用额外的标准差从高斯分布中采样值,围绕这个均值。随着训练的进行,标准差逐渐减小,在推理时我们只评估均值(即方差为0的分布)。
15.2.3 评论家和优势
评论家由值函数表示,该函数预测从状态获得的预期累积奖励。
它的目标是最小化平方优势。
优势函数基于,其目标是评估累积奖励平均值的偏差。也就是说,我们有兴趣估计通过做出的决策在多大程度上改善了随机决策(再次通过不变的先前网络状态进行评估)。我们使用所谓的广义优势估计(GAE){cite}schulman2015high来计算:
这里的表示在时间步获得的奖励,表示轨迹的总长度。和是两个超参数,它们影响从远期对奖励和状态值预测对优势计算的影响。它们通常被设置为小于1的值。
上述公式中的表示对真实优势的有偏估计。因此,GAE可以理解为从当前时间步到轨迹结束的这些估计的折现累积和。
15.3 在反问题中的应用
强化学习广泛应用于多个决策问题构建的轨迹优化。然而,在物理系统和偏微分方程的背景下,强化学习算法同样具有吸引力。在这种情况下,它们可以通过生成完整轨迹并通过将最终逼近与目标进行比较来操作,类似于监督单射击方法。
然而,这些方法在优化方式上存在差异。例如,像PPO这样的强化学习算法尝试通过将随机偏移量添加到演员选择的动作中来在训练过程中探索行动空间。这样,算法可以发现比以前更精细的新行为模式。
生成的力的长期效应如何被考虑也可以因物理系统而异。在具有可微分物理(DP)损失的控制力估计器设置中,如在{doc}diffphys-code-burgers中讨论的那样,这些依赖关系通过将损失梯度通过仿真步骤传递回以前的时间步来处理。相反,强化学习通常将环境视为没有梯度信息的黑盒子。当使用PPO时,值估计器网络被用来通过预测任何动作对未来系统演变的影响来跟踪长期依赖关系。
在以Burgers方程为物理环境的情况下,轨迹生成过程可以总结如下。它展示了环境的仿真步骤和代理的神经网络评估是如何交错的:
上标(通常)表示参考或目标量,因此这里表示速度目标。对于PDE的连续动作空间,直接计算一个力的动作,而不是一组不同动作概率的离散集合。
奖励的计算方式与DP方法中的损失类似:它由两部分组成,其中一部分相当于应用力的负平方范数,并在每个时间步骤给出。另一部分添加了一个惩罚,该惩罚与每个轨迹结束时的最终逼近和目标状态之间的距离成比例。

15.4 实现
下面,我们将描述一种实现基于PPO的物理系统RL训练的方法。这个实现也是下一节笔记本{doc}reinflearn-code的基础。虽然这个笔记本提供了一个实际的例子,并与DP训练进行了比较,但我们首先会在下面给出一个更通用的概述。
为了训练一个强化学习代理来控制一个PDE-governed系统,物理模型必须被形式化为一个RL环境。我们在接下来使用的stable-baselines3框架中,使用了一个向量化版本的OpenAI gym环境来实现PPO训练。这样,可以并行地在多个轨迹上进行回滚收集,以更好地利用资源和提高时间效率。向量化环境需要定义观察和动作空间,即代理策略的输入和输出空间。在我们的情况下,前者包括当前物理状态和目标状态,例如速度场,沿着它们的通道维度堆叠。另外一个通道添加了自模拟开始以来经过的时间除以总轨迹长度。动作空间(输出)包括速度场每个单元格的一个力值。
向量化环境中最相关的方法是reset、step_async、step_wait和render。其中,reset用于通过计算初始状态和目标状态并返回每个向量化实例的第一个观测来启动新轨迹。由于这些实例在其他应用程序中不必同步完成轨迹,reset必须在进入终止状态时从环境内部调用。 step_async和step_wait是step方法的两个主要部分,该方法采取行动,将其应用于速度场并执行物理模型的一次迭代。异步和等待的分割使支持在单独的线程上运行每个实例的向量化环境成为可能。但是,在我们的方法中并不需要这样做,因为phiflow在内部处理批次的模拟。调用render方法以显示训练结果,实时显示重构的轨迹或将其呈现到文件中。
由于演员和评论家网络的输出空间差异很大,我们为每个网络使用不同的体系结构。生成行动的网络使用Holl等人的网络体系结构的变体,与那里执行行动的函数一致。另一个网络由一系列内核大小为3的卷积组成,每个卷积后跟一个内核大小为2且步幅为2的最大池化层。在这种方式下采样特征图至一个值后,最终的全连接层合并所有通道,生成预测状态值。
在下一章的示例实现中,BurgersTraining类在内部管理此培训的所有方面,包括代理和环境的设置,并将训练模型和监视日志存储到磁盘。它还包括上述Burgers方程环境的变体,该环境使用预定义集合中的数据,而不是计算随机轨迹。在训练期间,代理在此环境中进行评估,以便能够更准确地将训练进度与DP方法进行比较。
下一章将使用此BurgersTraining类来运行完整的PPO场景,评估其性能,并将其与使用物理系统更多领域知识的方法进行比较,即基于梯度的控制培训与DP方法。
接下来,我们将以Burgers方程作为强化学习(RL)的测试平台来针对反问题。该设置类似于之前使用可微物理(DP)训练针对的反问题(参见{doc}diffphys-code-control),因此我们将在下面直接进行比较。与之前类似,Burgers方程是简单但非线性的,具有有趣的动力学,因此是RL实验的一个良好起点。在接下来的过程中,目标是训练一个控制力估计网络,该网络应该预测生成两个给定状态之间平滑过渡所需的力。
16.1 概述
强化学习描述了一个代理在感知环境并在其中采取行动的过程。它旨在最大化代理通过环境采取的行动所获得的奖励累积和。因此,代理通过经验学习在不同情况下采取哪些行动。近端策略优化 (PPO)是一种广泛使用的强化学习算法,描述了两个神经网络:一个策略神经网络根据给定的观测选择行动,一个值估计网络评估这些状态的奖励潜力。这些值估计形成了策略网络的损失,即所选行动带来的奖励潜力变化。
本笔记本演示了如何将PPO强化学习应用于Burgers方程的控制问题。与DP方法相比,RL方法没有可微分的物理求解器,它是无模型的。然而,值估计神经网络的目标是弥补这种求解器的缺失,因为它试图捕捉单个行动的长期效应。因此,以下代码示例应该回答一个有趣的问题:无模型PPO强化学习能否匹配基于模型的DP训练的性能。我们将比较学习速度和所需力量的数量。
16.2 软件安装
本示例使用强化学习框架stable_baselines3,其中采用PPO作为强化学习算法。
对于物理仿真,使用可微分PDE求解器ΦFlow的1.5.1版本。在完成RL训练后,我们还将使用“控制力估计器”(CFE)网络从{doc}diffphys-code-control(由{cite}holl2019pdecontrol引入)引入可微分物理方法进行额外比较。
!pip install stable-baselines3==1.1 phiflow==1.5.1
!git clone https://github.com/Sh0cktr4p/PDE-Control-RL.git
!git clone https://github.com/holl-/PDE-Control.git
现在我们可以导入必要的模块。由于这个示例的范围比较大,需要加载相当多的模块。
import sys; sys.path.append('PDE-Control/src'); sys.path.append('PDE-Control-RL/src')
import time, csv, os, shutil
from tensorboard.backend.event_processing.event_accumulator import EventAccumulator
from phi.flow import *
import burgers_plots as bplt
import matplotlib.pyplot as plt
from envs.burgers_util import GaussianClash, GaussianForce
16.3 数据生成
首先,我们生成一个数据集用于训练可微分物理模型。我们还将使用它来在训练期间和训练后评估两种方法的性能。下面的代码模拟了1000个情况(即phiflow“场景”),并将其中的100个作为验证和测试用例。剩下的800个用于训练。
DOMAIN = Domain([32], box=box[0:1]) # Size and shape of the fields
VISCOSITY = 0.003
STEP_COUNT = 32 # Trajectory length
DT = 0.03
DIFFUSION_SUBSTEPS = 1
DATA_PATH = 'forced-burgers-clash'
SCENE_COUNT = 1000
BATCH_SIZE = 100
TRAIN_RANGE = range(200, 1000)
VAL_RANGE = range(100, 200)
TEST_RANGE = range(0, 100)
for batch_index in range(SCENE_COUNT // BATCH_SIZE):
scene = Scene.create(DATA_PATH, count=BATCH_SIZE)
print(scene)
world = World()
u0 = BurgersVelocity(
DOMAIN,
velocity=GaussianClash(BATCH_SIZE),
viscosity=VISCOSITY,
batch_size=BATCH_SIZE,
name='burgers'
)
u = world.add(u0, physics=Burgers(diffusion_substeps=DIFFUSION_SUBSTEPS))
force = world.add(FieldEffect(GaussianForce(BATCH_SIZE), ['velocity']))
scene.write(world.state, frame=0)
for frame in range(1, STEP_COUNT + 1):
world.step(dt=DT)
scene.write(world.state, frame=frame)
输出:
forced-burgers-clash/sim_000000
forced-burgers-clash/sim_000100
forced-burgers-clash/sim_000200
forced-burgers-clash/sim_000300
forced-burgers-clash/sim_000400
forced-burgers-clash/sim_000500
forced-burgers-clash/sim_000600
forced-burgers-clash/sim_000700
forced-burgers-clash/sim_000800
forced-burgers-clash/sim_000900
16.4 通过强化学习进行训练
接下来我们建立强化学习环境。PPO方法使用一个专门的价值估计网络(“评论家”)来预测从某个状态产生的奖励总和。然后使用这些预测的奖励来更新策略网络(“演员”),类似于{doc}diffphys-code-control中的CFE网络,预测用于控制模拟的力。
from experiment import BurgersTraining
N_ENVS = 10 # On how many environments to train in parallel, load balancing
FINAL_REWARD_FACTOR = STEP_COUNT # Penalty for not reaching the goal state
STEPS_PER_ROLLOUT = STEP_COUNT * 10 # How many steps to collect per environment between agent updates
N_EPOCHS = 10 # How many epochs to perform during each agent update
RL_LEARNING_RATE = 1e-4 # Learning rate for agent updates
RL_BATCH_SIZE = 128 # Batch size for agent updates
RL_ROLLOUTS = 500 # Number of iterations for RL training
为了开始训练,我们创建一个管理环境和代理的训练器对象。此外,还创建了一个用于存储模型、日志和超参数的目录。这样,可以使用相同的配置在任何后续时间继续训练。如果在exp_name中指定的模型文件夹已经存在,则加载其中的代理;否则,创建一个新的代理。对于PPO强化学习算法,使用stable_baselines3的实现。训练器类作为该系统的包装器。在底层,创建了一个BurgersEnv gym环境的实例,该环境加载到PPO算法中。它生成随机的初始状态,预计算相应的地面真实模拟,并处理受代理行动影响的系统演化。此外,训练器定期通过加载使用验证集的初始和目标状态的不同环境来评估性能。
16.5 Gym环境
Gym环境规范提供了利用代理交互的接口。实现它的环境必须指定观察和动作空间,它们表示代理策略的输入和输出空间。此外,它们还必须定义一组方法,其中最重要的有 reset、step 和 render。
reset在轨迹结束后被调用,以将环境重置为初始状态,并返回相应的观察结果。step获取代理给出的行动,并将环境迭代到下一个状态。它返回所得到的观察结果、收到的奖励、确定是否达到终端状态的标志以及用于调试和日志记录信息的字典。render被调用以以环境创建者指定的方式显示当前环境状态。此函数可用于检查训练结果。
与默认的 gym 环境相比,stable-baselines3 通过提供支持向量化环境的接口进行了扩展。这使得可以对多个轨迹同时计算前馈传播,从而由于更好的资源利用而增加时间效率。在实践中,这意味着这些方法现在在观测结果、行动、奖励、终端状态标志和信息字典的向量上运行。步骤方法分为 step_async 和 step_wait,使每个环境实例能够在不同线程上运行成为可能。
16.6 物理仿真
Burgers方程的环境包含由phiflow提供的Burgers物理对象。状态在内部存储为BurgersVelocity对象。为了创建初始状态,环境以与上面显示的数据集生成过程相同的方式生成一批随机字段。观测空间由叠加在通道维度中的当前状态和目标状态的速度场组成,另一个通道指定当前时间步长。动作以覆盖每个速度值的一维阵列的形式进行。step方法调用物理对象将内部状态提前一个时间步长,也将这些动作应用为FieldEffect。
奖励包括一个等于每个时间步长产生的力的平方范数的惩罚。此外,在每个轨迹的末尾减去按预定义因子(FINAL_REWARD_factor)缩放的到目标场的距离。然后用对奖励平均值和标准差的运行估计对奖励进行归一化。
16.7 神经网络设置
我们使用两种不同的神经网络架构分别用于演员和评论家。前者使用{cite}holl2019pdecontrol中的U-Net变体,而后者由一系列1D卷积和池化层组成,将特征映射大小降至1。最后的操作是使用核大小为1的卷积将特征映射组合并保留一个输出值。然后,CustomActorCriticPolicy类使得可以使用这两个独立的网络架构来进行强化学习代理。
默认情况下,代理存储在PDE-Control-RL/networks/rl-models/bench中,并在存在时加载。 (如果需要,将下面的path替换为新的路径以从新模型开始。)由于训练时间较长,因此我们在这里使用预先训练的代理。它已经训练了3500个迭代,因此我们只需通过另外的RL_ROLLOUTS=500迭代进行“微调”。这些通常需要大约2个小时,因此几乎18个小时的总训练时间对于交互式测试来说太长了。 (但是,如果您拥有资源,此处提供的代码包含从头开始训练模型的所有内容。)
rl_trainer = BurgersTraining(
path='PDE-Control-RL/networks/rl-models/bench', # Replace path to train a new model
domain=DOMAIN,
viscosity=VISCOSITY,
step_count=STEP_COUNT,
dt=DT,
diffusion_substeps=DIFFUSION_SUBSTEPS,
n_envs=N_ENVS,
final_reward_factor=FINAL_REWARD_FACTOR,
steps_per_rollout=STEPS_PER_ROLLOUT,
n_epochs=N_EPOCHS,
learning_rate=RL_LEARNING_RATE,
batch_size=RL_BATCH_SIZE,
data_path=DATA_PATH,
val_range=VAL_RANGE,
test_range=TEST_RANGE,
)
Tensorboard log path: PDE-Control-RL/networks/rl-models/bench/tensorboard-log
Loading existing agent from PDE-Control-RL/networks/rl-models/bench/agent.zip
下面的单元格是可选的,但对于调试非常有用:它在笔记本内打开_tensorboard_以显示训练的进度。如果在不同位置创建了一个新模型,请相应地更改路径。当恢复预训练代理的学习过程时,新运行将在tensorboard中单独显示(通过齿轮按钮启用重新加载)。
名为“forces”的图表显示了网络生成的总力量随着训练的演变情况。“rew_unnormalized”显示了未进行上述归一化步骤的奖励值。对应的归一化值在“rollout/ep_rew_mean”下方显示。“val_set_forces”概述了代理在验证集上的表现。
%load_ext tensorboard
%tensorboard --logdir PDE-Control-RL/networks/rl-models/bench/tensorboard-log
现在我们已经准备好开始对代理进行训练了。强化学习方法需要进行多次迭代来探索环境。因此,下一个单元格通常需要多个小时才能执行完毕(500次模拟需要大约2小时)。
rl_trainer.train(n_rollouts=RL_ROLLOUTS, save_freq=50)
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
Storing agent and hyperparameters to disk...
16.8 RL 评估
现在我们有了一个训练好的模型,让我们来看看结果。最左边的图显示了强化学习代理的结果。作为参考,在其旁边显示了地面真相,即代理应该重建的轨迹,以及未受控制的模拟,其中系统遵循其自然演化。
TEST_SAMPLE = 0 # Change this to display a reconstruction of another scene
rl_frames, gt_frames, unc_frames = rl_trainer.infer_test_set_frames()
fig, axs = plt.subplots(1, 3, figsize=(18.9, 9.6))
axs[0].set_title("Reinforcement Learning"); axs[1].set_title("Ground Truth"); axs[2].set_title("Uncontrolled")
for plot in axs:
plot.set_ylim(-2, 2); plot.set_xlabel('x'); plot.set_ylabel('u(x)')
for frame in range(0, STEP_COUNT + 1):
frame_color = bplt.gradient_color(frame, STEP_COUNT+1);
axs[0].plot(rl_frames[frame][TEST_SAMPLE,:], color=frame_color, linewidth=0.8)
axs[1].plot(gt_frames[frame][TEST_SAMPLE,:], color=frame_color, linewidth=0.8)
axs[2].plot(unc_frames[frame][TEST_SAMPLE,:], color=frame_color, linewidth=0.8)
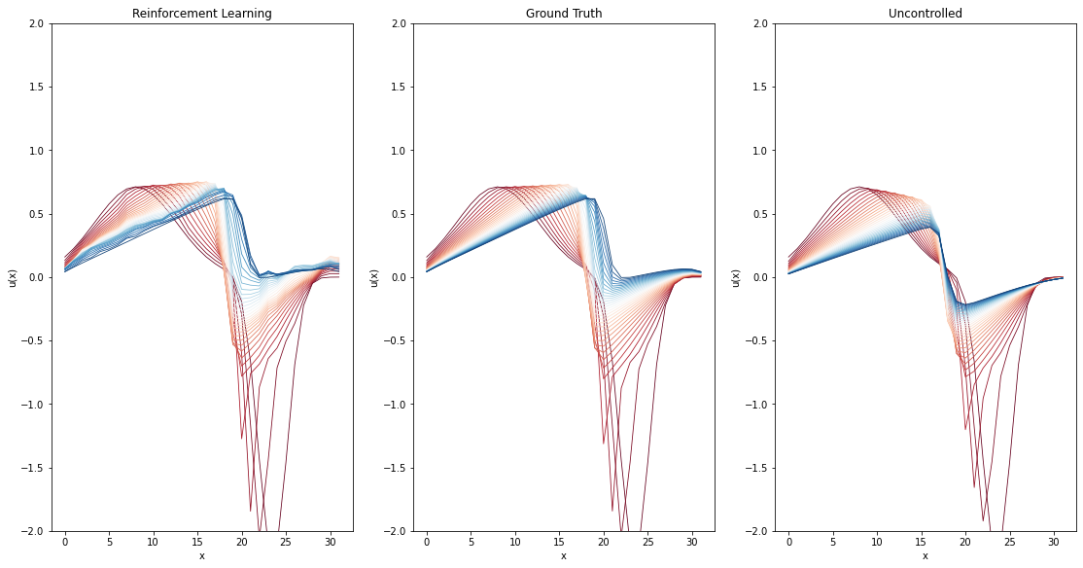
正如我们所看到的,经过训练的强化学习代理能够相当好地重构轨迹。然而,它们仍然显著比真实情况不够平滑。
16.9 可微物理训练
为了对强化学习方法的结果进行分类,我们现在将它们与可微分物理训练方法进行比较。与包括第二个_OP_网络的完整方法相比,我们在这里旨在直接控制。OP网络代表一个独立的“物理预测器”,在与RL版本进行比较时为公平起见,我们省略了它。
DP方法可以访问由可微分求解器提供的梯度数据,从而可以跟踪多个时间步长的损失,并使模型更好地理解所生成力的长期效应。另一方面,强化学习算法不像DP算法那样受训练集大小的限制,因为新的训练样本是在策略上生成的。然而,这也在训练期间引入了额外的模拟开销,可能会增加收敛所需的时间。
from control.pde.burgers import BurgersPDE
from control.control_training import ControlTraining
from control.sequences import StaggeredSequence
Could not load resample cuda libraries: CUDA binaries not found at /usr/local/lib/python3.7/dist-packages/phi/tf/cuda/build/resample.so. Run "python setup.py cuda" to compile them
下面的单元格设置用于训练模型或加载现有模型检查点。
dp_app = ControlTraining(
STEP_COUNT,
BurgersPDE(DOMAIN, VISCOSITY, DT),
datapath=DATA_PATH,
val_range=VAL_RANGE,
train_range=TRAIN_RANGE,
trace_to_channel=lambda trace: 'burgers_velocity',
obs_loss_frames=[],
trainable_networks=['CFE'],
sequence_class=StaggeredSequence,
batch_size=100,
view_size=20,
learning_rate=1e-3,
learning_rate_half_life=1000,
dt=DT
).prepare()
App created. Scene directory is /root/phi/model/control-training/sim_000000 (INFO), 2021-08-04 10:11:58,466n
Sequence class: <class 'control.sequences.StaggeredSequence'> (INFO), 2021-08-04 10:12:01,449n
Partition length 32 sequence (from 0 to 32) at frame 16
Partition length 16 sequence (from 0 to 16) at frame 8
Partition length 8 sequence (from 0 to 8) at frame 4
Partition length 4 sequence (from 0 to 4) at frame 2
Partition length 2 sequence (from 0 to 2) at frame 1
Execute -> 1
Execute -> 2
Partition length 2 sequence (from 2 to 4) at frame 3
Execute -> 3
Execute -> 4
Partition length 4 sequence (from 4 to 8) at frame 6
Partition length 2 sequence (from 4 to 6) at frame 5
Execute -> 5
Execute -> 6
Partition length 2 sequence (from 6 to 8) at frame 7
Execute -> 7
Execute -> 8
Partition length 8 sequence (from 8 to 16) at frame 12
Partition length 4 sequence (from 8 to 12) at frame 10
Partition length 2 sequence (from 8 to 10) at frame 9
Execute -> 9
Execute -> 10
Partition length 2 sequence (from 10 to 12) at frame 11
Execute -> 11
Execute -> 12
Partition length 4 sequence (from 12 to 16) at frame 14
Partition length 2 sequence (from 12 to 14) at frame 13
Execute -> 13
Execute -> 14
Partition length 2 sequence (from 14 to 16) at frame 15
Execute -> 15
Execute -> 16
Partition length 16 sequence (from 16 to 32) at frame 24
Partition length 8 sequence (from 16 to 24) at frame 20
Partition length 4 sequence (from 16 to 20) at frame 18
Partition length 2 sequence (from 16 to 18) at frame 17
Execute -> 17
Execute -> 18
Partition length 2 sequence (from 18 to 20) at frame 19
Execute -> 19
Execute -> 20
Partition length 4 sequence (from 20 to 24) at frame 22
Partition length 2 sequence (from 20 to 22) at frame 21
Execute -> 21
Execute -> 22
Partition length 2 sequence (from 22 to 24) at frame 23
Execute -> 23
Execute -> 24
Partition length 8 sequence (from 24 to 32) at frame 28
Partition length 4 sequence (from 24 to 28) at frame 26
Partition length 2 sequence (from 24 to 26) at frame 25
Execute -> 25
Execute -> 26
Partition length 2 sequence (from 26 to 28) at frame 27
Execute -> 27
Execute -> 28
Partition length 4 sequence (from 28 to 32) at frame 30
Partition length 2 sequence (from 28 to 30) at frame 29
Execute -> 29
Execute -> 30
Partition length 2 sequence (from 30 to 32) at frame 31
Execute -> 31
Execute -> 32
Target loss: Tensor("truediv_1:0", shape=(), dtype=float32) (INFO), 2021-08-04 10:13:10,701n
Force loss: Tensor("Sum_97:0", shape=(), dtype=float32) (INFO), 2021-08-04 10:13:14,221n
Setting up loss (INFO), 2021-08-04 10:13:14,223n
Preparing data (INFO), 2021-08-04 10:13:51,128n
INFO:tensorflow:Summary name Total Force is illegal; using Total_Force instead.
Initializing variables (INFO), 2021-08-04 10:13:51,156n
Model variables contain 0 total parameters. (INFO), 2021-08-04 10:13:55,961n
Validation (000000): Learning_Rate: 0.001, Loss_reg_unscaled: 205.98526, Loss_reg_scale: 1.0, Loss: 0.0, Total Force: 393.8109 (INFO), 2021-08-04 10:14:32,455n
现在我们可以执行模型训练。这个单元格的执行时间也比较长 (对于 1000 次迭代大约需要 2 小时)。
DP_TRAINING_ITERATIONS = 10000 # Change this to change training duration
dp_training_eval_data = []
start_time = time.time()
for epoch in range(DP_TRAINING_ITERATIONS):
dp_app.progress()
# Evaluate validation set at regular intervals to track learning progress
# Size of intervals determined by RL epoch count per iteration for accurate comparison
if epoch % N_EPOCHS == 0:
f = dp_app.infer_scalars(VAL_RANGE)['Total Force'] / DT
dp_training_eval_data.append((time.time() - start_time, epoch, f))
经过训练的模型和关于迭代次数和墙上时间的验证性能 val_forces.csv 被保存到磁盘上:
DP_STORE_PATH = 'networks/dp-models/bench'
if not os.path.exists(DP_STORE_PATH):
os.makedirs(DP_STORE_PATH)
# store training progress information
with open(os.path.join(DP_STORE_PATH, 'val_forces.csv'), 'at') as log_file:
logger = csv.DictWriter(log_file, ('time', 'epoch', 'forces'))
logger.writeheader()
for (t, e, f) in dp_training_eval_data:
logger.writerow({'time': t, 'epoch': e, 'forces': f})
dp_checkpoint = dp_app.save_model()
shutil.move(dp_checkpoint, DP_STORE_PATH)
'networks/dp-models/bench/checkpoint_00010000'
或者,取消注释下面单元格中的代码以加载现有的网络模型。
# dp_path = 'PDE-Control-RL/networks/dp-models/bench/checkpoint_00020000/'
# networks_to_load = ['OP2', 'OP4', 'OP8', 'OP16', 'OP32']
# dp_app.load_checkpoints({net: dp_path for net in networks_to_load})
与强化学习版本类似,下一个单元格绘制了一个示例,以视觉方式展示基于差分隐私的模型的表现。最左边的图表再次显示了学习结果,这次是基于差分隐私的模型。与上述情况类似,其他两个图表显示了真实结果和自然演变。
dp_frames = dp_app.infer_all_frames(TEST_RANGE)
dp_frames = [s.burgers.velocity.data for s in dp_frames]
_, gt_frames, unc_frames = rl_trainer.infer_test_set_frames()
TEST_SAMPLE = 0 # Change this to display a reconstruction of another scene
fig, axs = plt.subplots(1, 3, figsize=(18.9, 9.6))
axs[0].set_title("Differentiable Physics")
axs[1].set_title("Ground Truth")
axs[2].set_title("Uncontrolled")
for plot in axs:
plot.set_ylim(-2, 2)
plot.set_xlabel('x')
plot.set_ylabel('u(x)')
for frame in range(0, STEP_COUNT + 1):
frame_color = bplt.gradient_color(frame, STEP_COUNT+1)
axs[0].plot(dp_frames[frame][TEST_SAMPLE,:], color=frame_color, linewidth=0.8)
axs[1].plot(gt_frames[frame][TEST_SAMPLE,:], color=frame_color, linewidth=0.8)
axs[2].plot(unc_frames[frame][TEST_SAMPLE,:], color=frame_color, linewidth=0.8)
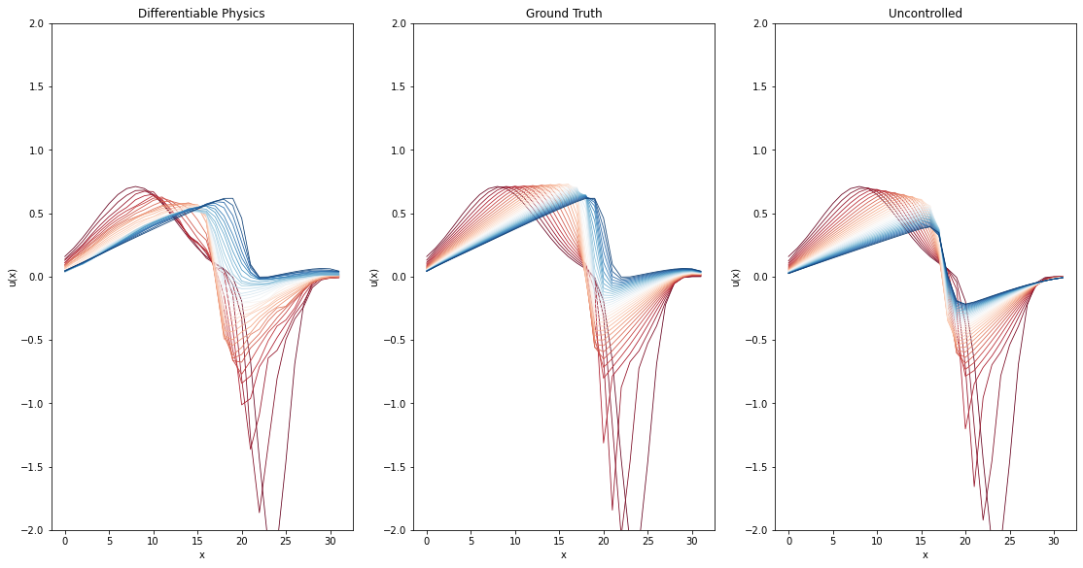
经过训练的DP模型还能够紧密地重构原始轨迹。此外,生成的结果似乎比使用RL代理更少有噪声。
因此,我们有了一个RL版本和一个DP版本,我们可以在下一节中进行更详细的比较。
16.10 RL 和 DP 的比较
接下来,通过生成的轨迹的视觉质量以及生成的力量数量进行两种方法的比较。后者提供了关于两种方法性能的见解,因为在训练过程中,两种方法都希望最小化这个度量标准。这也很重要,因为通过在最后一个时间步骤应用巨大的力量,任务可以轻松解决。因此,理想的解决方案考虑了PDE的动态,尽可能地应用少量的力量。因此,这个度量标准非常好,可以衡量网络对基础物理环境(在这个例子中是Burgers方程)的学习情况。
import utils
import pandas as pd
16.10.1 轨迹比较
为了比较结果轨迹,我们使用任一方法从测试集生成轨迹。同时,我们收集测试集场的真实模拟和自然演化。
rl_frames, gt_frames, unc_frames = rl_trainer.infer_test_set_frames()
dp_frames = dp_app.infer_all_frames(TEST_RANGE)
dp_frames = [s.burgers.velocity.data for s in dp_frames]
frames = {
(0, 0): ('Ground Truth', gt_frames),
(0, 1): ('Uncontrolled', unc_frames),
(1, 0): ('Reinforcement Learning', rl_frames),
(1, 1): ('Differentiable Physics', dp_frames),
}
TEST_SAMPLE = 0 # Specifies which sample of the test set should be displayed
def plot(axs, xy, title, field):
axs[xy].set_ylim(-2, 2); axs[xy].set_title(title)
axs[xy].set_xlabel('x'); axs[xy].set_ylabel('u(x)')
label = 'Initial state (red), final state (blue)'
for step_idx in range(0, STEP_COUNT + 1):
color = bplt.gradient_color(step_idx, STEP_COUNT+1)
axs[xy].plot(
field[step_idx][TEST_SAMPLE].squeeze(), color=color, linewidth=0.8, label=label)
label = None
axs[xy].legend()
fig, axs = plt.subplots(2, 2, figsize=(12.8, 9.6))
for xy in frames:
plot(axs, xy, *frames[xy])
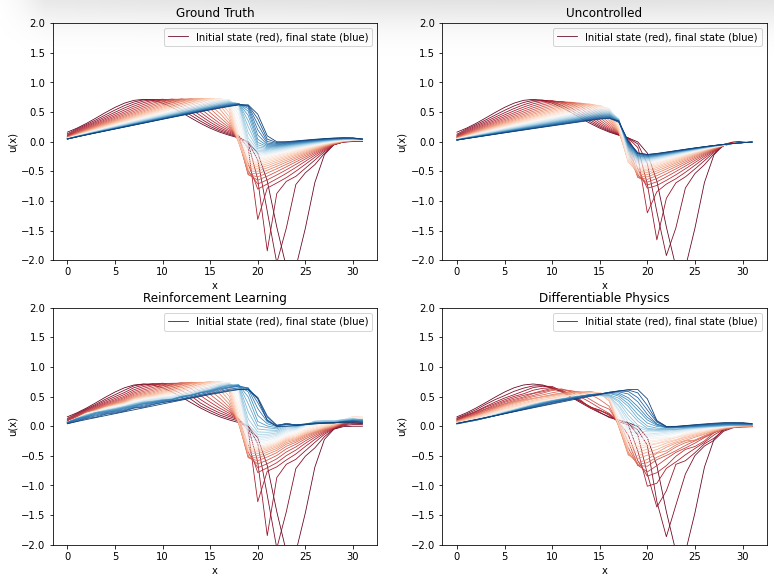
这张图将上面两个训练后的图表连接在一起。我们再次看到,可微物理方法似乎比强化学习代理生成的轨迹更少噪声,而两者都能近似地逼近真实情况。
16.10.2 生成力的比较
接下来,我们计算各个方法产生并应用于测试集轨迹的力。
gt_forces = utils.infer_forces_sum_from_frames(
gt_frames, DOMAIN, DIFFUSION_SUBSTEPS, VISCOSITY, DT
)
dp_forces = utils.infer_forces_sum_from_frames(
dp_frames, DOMAIN, DIFFUSION_SUBSTEPS, VISCOSITY, DT
)
rl_forces = rl_trainer.infer_test_set_forces()
Sanity check - maximum deviation from target state: 0.000000
Sanity check - maximum deviation from target state: 0.000011
首先,我们将比较RL和DP方法生成的力的总和,并将其与实际情况进行比较。
plt.figure(figsize=(8, 6))
plt.bar(
["Reinforcement Learning", "Differentiable Physics", "Ground Truth"],
[np.sum(rl_forces), np.sum(dp_forces), np.sum(gt_forces)],
color = ["#0065bd", "#e37222", "#a2ad00"],
align='center', label='Absolute forces comparison' )
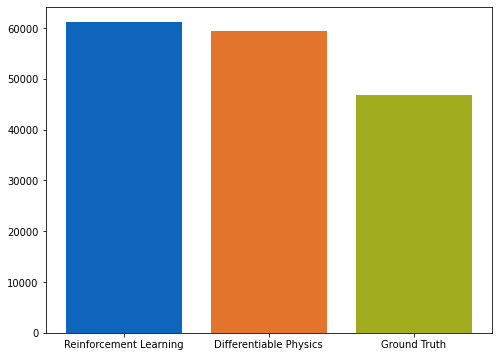
如图所示的条形图所示,DP方法学习应用的力略低于RL模型。
由于两种方法在达到最终目标状态方面表现相当,因此这是我们用来比较两种方法性能的主要数量。接下来,方法生成的力也与各样本的真实情况进行了视觉比较。放置在蓝线上方的点表示分析的深度学习方法比地面实况产生更强的力,反之亦然。
plt.figure(figsize=(12, 9))
plt.scatter(gt_forces, rl_forces, color="#0065bd", label='RL')
plt.scatter(gt_forces, dp_forces, color="#e37222", label='DP')
plt.plot([x * 100 for x in range(15)], [x * 100 for x in range(15)], color="#a2ad00", label='Same forces as original')
plt.xlabel('ground truth'); plt.ylabel('reconstruction')
plt.xlim(0, 1200); plt.ylim(0, 1200); plt.grid(); plt.legend()
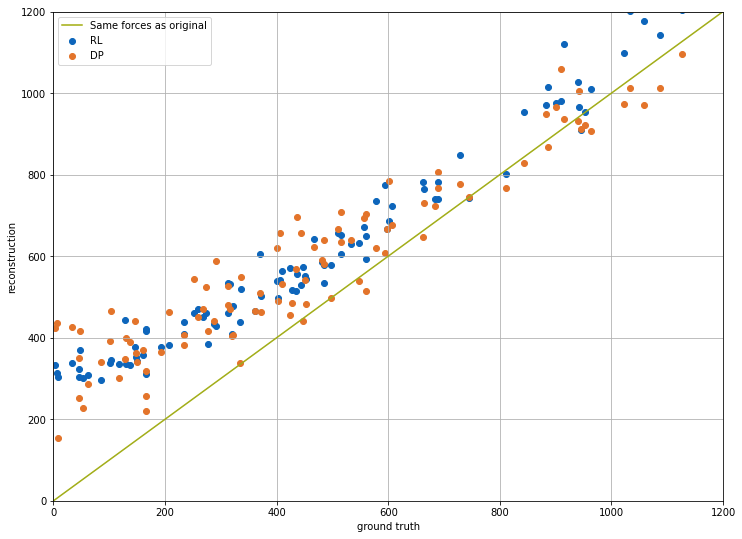
图表显示,DP训练运行的橙色点通常更接近对角线 - 即,该网络学会了生成更接近真实值的力。
下图显示了所有强化学习、可微分物理和基准真值在个体样本上的表现。
w=0.25; plot_count=20 # How many scenes to show
plt.figure(figsize=(12.8, 9.6))
plt.bar( [i - w for i in range(plot_count)], rl_forces[:plot_count], color="#0065bd", width=w, align='center', label='RL' )
plt.bar( [i for i in range(plot_count)], dp_forces[:plot_count], color="#e37222", width=w, align='center', label='DP' )
plt.bar( [i + w for i in range(plot_count)], gt_forces[:plot_count], color="#a2ad00", width=w, align='center', label='GT' )
plt.xlabel('Scenes'); plt.xticks(range(plot_count))
plt.ylabel('Forces'); plt.legend(); plt.show()
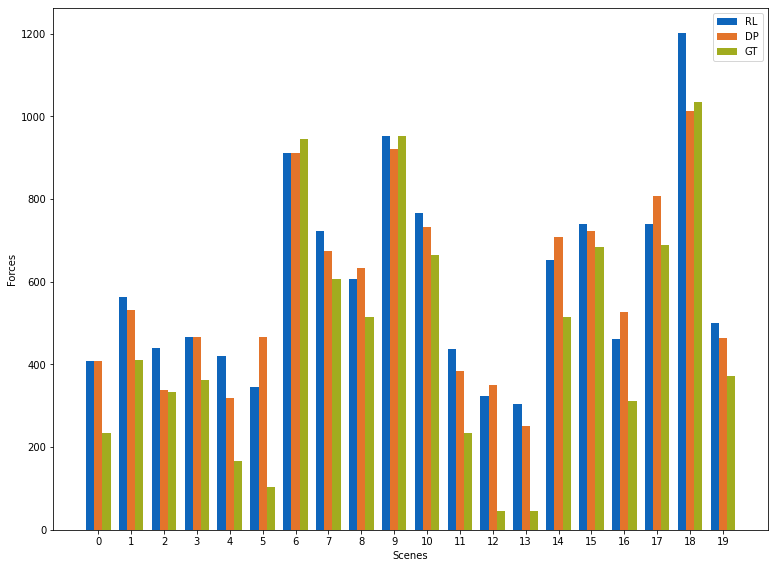
16.11 训练进度比较
虽然以上设置的主要目标是力量大小方面的控制质量,但在训练时,两种方法的行为方式存在有趣的差异。物理无感知的强化学习训练和具有紧密耦合求解器的DP方法的主要差异在于后者的收敛速度明显更快。即,数值求解器提供的梯度比RL过程的无指导探索提供更好的学习信号。另一方面,RL训练的行为部分可以归因于训练数据收集的策略性和强化学习技术的“蛮力”探索。
下一个单元格将可视化两种方法在墙时方面的训练进展。
def get_dp_val_set_forces(experiment_path):
path = os.path.join(experiment_path, 'val_forces.csv')
table = pd.read_csv(path)
return list(table['time']), list(table['epoch']), list(table['forces'])
rl_w_times, rl_step_nums, rl_val_forces = rl_trainer.get_val_set_forces_data()
dp_w_times, dp_epochs, dp_val_forces = get_dp_val_set_forces(DP_STORE_PATH)
plt.figure(figsize=(12, 5))
plt.plot(np.array(rl_w_times) / 3600, rl_val_forces, color="#0065bd", label='RL')
plt.plot(np.array(dp_w_times) / 3600, dp_val_forces, color="#e37222", label='DP')
plt.xlabel('Wall time (hours)'); plt.ylabel('Forces')
plt.ylim(0, 1500); plt.grid(); plt.legend()
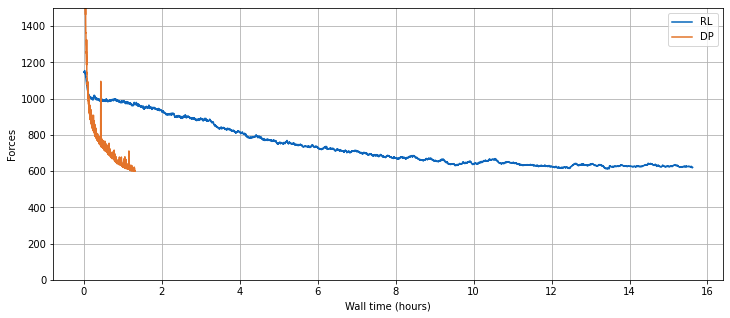
综上所述,与可微分物理方法相比,PPO强化学习施加的力更高。因此,PPO得到的学习解决方案质量略微劣。此外,在强化学习情况下,收敛所需的时间显著更长(无论是在墙上的时间还是在训练迭代中)。
16.12 下一步
- 观察超参数(如学习率)不同取值对训练过程的影响
- 使用不同分辨率的场,并比较两种方法的差异。更高的分辨率会使物理动力学更加复杂,因此更难控制
- 在不同环境参数(如粘度、dt)的设置中使用训练好的模型,并测试它们的泛化能力
下面,我们将对迄今为止所提出的公式的一些基本方面提出质疑,即通过梯度计算的更新步骤。概括地说,前几章介绍的方法要么是纯粹的_监督_训练,要么是将物理模型作为物理损失项整合进来,要么是通过嵌入训练图的可微物理(DP)算子将其包含在内。后两种方法与本书的内容更为相关。它们有相似之处,但在损失项的情况下,物理评估只需要在训练时进行。对于 DP 方法,通常在推理时也会使用求解器本身,从而实现对 NN 和数值求解器的端到端训练。这三种方法都使用一阶导数来驱动优化和学习过程,后两种方法还使用一阶导数来计算物理项。从深度学习的角度来看,这是很自然的选择,但我们完全没有质疑这是否是最佳选择。
经过上述介绍,我们也就不觉得奇怪了:下面章节的核心观点是,对于涉及物理量的学习问题,常规梯度可能是次优选择。事实证明,有监督和DP梯度各有利弊,同时也为了解物理算子的定制方法留出了空间。特别是,我们将展示 DP 梯度的缩放问题如何影响 NN 训练(如 {cite}holl2021pg 中所述),并重新探讨多模态解的问题。最后,我们将解释防止这些问题的几种替代方法。
下面,我们将按以下步骤进行:
- 展示不同优化器的特性以及相关的缩放问题如何对 NN 训练产生负面影响。
- 找出迄今为止我们的 GD 或 Adam 训练运行中存在的问题。剧透:它们缺少一个反演过程来使训练与缩放无关。
- 然后,我们将解释缓解这些问题的两种替代方案:一种是分析全反演,另一种是数值半反演方案。
17.1 问题的关键
在深入探讨不同优化器的细节之前,下面的段落应该能让我们直观地了解为什么这种反演很重要。如上所述,迄今为止讨论的所有方法都使用梯度,而梯度存在基本的缩放问题:即使是相对简单的线性情况,梯度的方向也可能被负向扭曲,从而阻碍向最小值的有效推进。(在非线性情况下,梯度的长度与离最小点的距离成反比,因此更难收敛)。
在一维空间中,可以通过调整学习率来缓解这个问题,但在高维空间中,问题变得非常明显。让我们考虑一个非常简单的二维玩具“物理”函数,它简单地将因子 应用于第二个分量,然后加上 损失:
\mathcal P(x_1,x_2) = \begin{bmatrix} x_1 \ \alpha ~ x_2 \end{bmatrix} \text{ 其中 } L(\mathcal P) = |\mathcal P|^2
对于 来说,一切都很简单:我们面对的是一个径向对称的损失曲面,而 和 的行为方式是一样的。梯度 垂直于损失分布的孤立线,因此使用 的更新会直接指向 0 处的最小值。这是我们处理经典深度学习场景的一种设置,比如大多数监督学习案例或分类问题。下图左侧为该示例的可视化示意图。
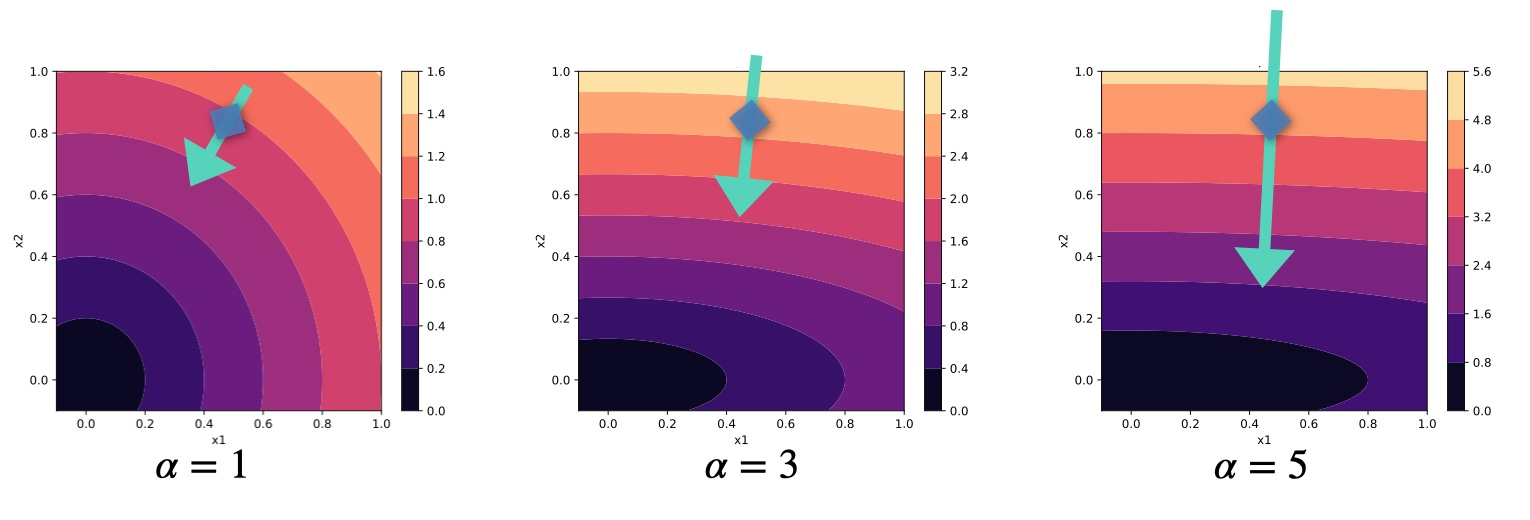
然而,在本书中,我们针对的是物理学习问题,因此我们在学习过程中融入了物理函数,这一点在可微分物理方法中已有详细讨论。这在本质上是不同的!物理过程几乎总是为不同的成分引入不同的缩放行为:物理状态的某些变化是敏感的,会产生巨大的反应,而另一些则几乎没有任何影响。在我们的玩具问题中,我们可以通过选择不同的 值来模拟这种情况,如上图的中间和右图所示。
对于较大的 ,远离最小值的损失曲面沿 逐渐陡峭。 与 的尺度差异越来越大。因此,梯度会沿着 增长。如果我们不想让优化结果爆炸,就需要选择一个较小的学习率 ,从而减少沿 的梯度。当然,梯度会与损失保持垂直。在这个例子中,我们会沿着 快速移动,直到接近 x 轴,然后才会非常缓慢地向左移动到最小值。更糟糕的是,正如我们将在下文中展示的,定期更新实际上应用的是缩放的平方!而在多维度的设置中,要找到一个好的学习率是非常困难的。因此,为了取得适当的进展,我们需要考虑多维函数中各分量的不同缩放比例。这就需要某种形式的反转,我们将在下文中详细介绍。
请注意,反转自然不意味着否定()。一个负梯度肯定会朝着错误的方向移动。我们需要一种仍指向损失递减的更新,但要考虑到不同比例的维度。因此,下面的核心目标将是 "尺度不变性"。
缩放不变性的定义:对给定函数进行尺度不变优化时,函数的不同参数(即标度)会产生相同的结果。
例如,对于我们上面的玩具问题,这意味着无论我们选择 的值是多少,优化轨迹都是相同的。

17.2 传统优化方法
现在,我们将对不同优化器的性能进行评估和讨论。和之前一样,让 成为标量损失函数,并进行最小化。我们的目标是根据输入参数 计算一个步长,用 表示。下面,我们将计算不同版本的 ,并用下标加以区分。
前几章中的所有 NN 都是通过反向传播的梯度下降(GD)训练的。在 PDE 求解器(模拟器) 中也使用了带有反向传播的梯度下降法,从而形成了 DP 训练方法。当简化设置并暂时忽略 NN 时,就会得到最小化问题 ,其中 。作为一个核心量,我们有损失函数 的复合梯度 :
由于符号使得阅读困难,而且我们实际上只处理转置的雅可比矩阵,因此在接下来的讨论中我们将省略符号。我们在前几章已经证明了使用是可行的,但在经典优化领域,除了梯度下降(GD)之外,还有其他更广泛使用的算法:比较流行的是所谓的拟牛顿方法,它们使用的更新方法有着本质的不同。因此,在接下来的讨论中,我们将重新审视GD以及拟牛顿方法和作为第三种选择的逆雅可比矩阵。我们将在理论层面上重点讨论不同方法的优缺点。其中,有趣的是讨论为什么尽管经典优化算法具有一些明显的优势,但在神经网络训练中并没有被广泛使用。
请注意,我们仅考虑多元函数,因此除非另有说明,否则所有符号都表示向量值表达式。
注:牛顿法或BFGS变体等技术常用于优化数值过程,因为它们可以提供更好的收敛速度和稳定性。这些方法同样采用梯度信息,但在计算更新步长时与GD有很大的区别,它们通常采用高阶导数。
17.3 梯度下降法
梯度下降(GD)的优化更新与目标函数对输入的导数成比例:
其中是标量学习率。
雅可比矩阵描述了损失是如何对输入的微小变化做出反应的。
令人惊讶的是,这种被广泛使用的更新方法存在一些不可取之处,我们将在接下来的内容中进行重点介绍。请注意,我们在(如{doc}supervised-airfoils)等有监督的设置中自然地应用了这种更新方法,我们也在可微分物理方法中使用了它。例如,在{doc}diffphys-code-sol中,我们计算了流体求解器的导数。在后一种情况下,我们仍然只更新了神经网络参数,但流体求解器的雅可比矩阵是方程{eq}GD-update的一部分,如{eq}loss-deriv所示。
我们将联合评估梯度下降法和其他几种方法在一系列类别中的处理方式:单位处理、函数敏感性和接近最优点的行为。虽然这些主题是相关的,但它们展示了这些方法之间的异同。
单位
GD的一个问题是其本质上错误地表示了维度。假设两个参数和具有不同的物理单位。那么GD参数更新的尺度与这些单位的倒数成比例,因为参数出现在GD更新的分母中()。学习率可以弥补这种差异,但由于和具有不同的单位,不存在一个单一的可以为两个参数产生正确的单位。
有人可能会认为神经网络的参数并不太重要,但从物理学的角度来看,它们的错误是令人不安的,并且暗示了一些更根本的问题。
函数敏感性
如上所述,当函数未经过归一化时,GD也存在固有问题。考虑上述玩具示例的简化版本,即仅包含函数。那么GD的参数更新与成比例,即,而的项甚至会达到量级。如果通过对进行归一化,一切都很好。但在实践中,我们经常会遇到,甚至更糟的是,这样我们的优化就会遇到麻烦。
更具体地说,如果我们观察损失的变化,那么GD的更新步骤中围绕的展开可以得到:。这个一阶步骤导致损失的变化为 。因此,损失的变化由导数的平方决定,这导致了上述提到的 因子。更糟糕的是,在实践中我们希望这里有一个归一化的量。对于梯度的缩放因子 ,我们希望我们的优化器计算一个类似于 的量,以便从梯度中得到可靠的更新。
这表明对于敏感函数,即在的小变化会导致的大变化的函数,梯度下降法(GD)会产生大的,这会导致的更大变化,从而导致梯度爆炸的问题。对于不敏感函数,即输入的大变化不会对输出产生太大变化的函数,梯度下降法会产生小的更新,这可能导致优化过程停滞不前,这就是经典的梯度消失问题。
这种敏感性问题在复杂函数中很容易出现,比如深度神经网络,其中的层通常没有完全归一化。归一化结合正确设置学习率可以在神经网络中在一定程度上抵消这种行为,但在优化物理模拟时这些工具是不可用的。在模拟中应用归一化除了在最后一个求解步骤之后,任何地方都会破坏模拟的状态。在实践中调整学习率也很困难,例如在同时优化不同时间步的模拟参数或者模拟输出相对于初始状态的幅度变化较大的情况下。
最优点附近的收敛
最终,任何可微函数的损失曲面在接近最优解时必然变得平坦,因为梯度在收敛时趋近于零。因此,当接近最优解时,,导致收敛速度缓慢。
这是一个重要的观点,我们将在下面重新讨论它。这也有些令人惊讶,但实际上它可以稳定训练。另一方面,它使得学习过程难以控制。
17.4 拟牛顿法
牛顿法利用梯度和Hessian矩阵的逆来进行更新。
在实践中更广泛使用的是拟牛顿方法,例如BFGS及其变种,它们近似于Hessian矩阵。然而由此产生的更新保持不变。作为进一步的改进,步长通常通过线搜索确定(我们暂时忽略这一步骤)。这种构造解决了上述梯度下降的一些问题,但也存在其他缺点。
单位和敏感性
拟牛顿方法相比于梯度下降法在物理单位处理方面提供了更好的解决方案。方程(1)中的准牛顿更新方法可以为所有需要优化的参数提供正确的单位。因此,可以保持无量纲。
现在考虑通过计算损失变化的情况,第二项正确地抵消了量,并留下了一个与有关的标量更新。回想一下梯度下降法部分的缩放因子的示例,牛顿方法中的逆海森矩阵成功地为我们提供了一个的因子来抵消我们更新的不良缩放。
最优点附近的收敛
当损失函数的曲面相对平坦时,拟牛顿法的收敛速度更快。它们不会减慢步伐,即使被固定。这要归功于逆Hessian矩阵的特征值,它们与Hessian矩阵的特征值成反比,因此随着损失曲面的平坦程度而增加。
复合函数中的一致性
到目前为止,拟牛顿方法解决了梯度下降法的两个缺点。然而,与梯度下降法类似,中间空间的更新仍然取决于之前的所有函数。这种行为源于复合函数的海森矩阵中梯度的非线性项。考虑一个函数组合,其中如上所述,并且还有一个额外的函数。
那么海森矩阵依赖于内部雅可比矩阵的平方。这意味着如果我们在反向传播步骤中使用这种更新,海森矩阵会受到反向传播链中_后续_函数的影响。因此,在计算梯度时,任何中间潜在空间的更新都是未知的。
依赖于海森矩阵
此外,从以上讨论可以明显看出拟牛顿方法的一个根本缺点是其对Hessian矩阵的依赖性。Hessian矩阵在目前讨论的所有改进中都起着至关重要的作用。
首先,明显的缺点是计算成本。尽管评估精确的Hessian矩阵只会在每个优化步骤中增加一个额外的遍历,但这个遍历涉及到比计算梯度更高维的张量。由于随参数数量的平方增长,对于大型系统来说,它的评估和求逆都变得非常昂贵。这就是拟牛顿方法在使用合理资源计算近似值时所付出的重要努力,但这仍然是一个核心问题。
上述拟合牛顿更新还需要_Hessian_矩阵的逆。因此,接近不可逆的Hessian通常会导致数值稳定性问题,而本质上不可逆的Hessian则需要退回到一阶GD更新。
拟牛顿方法的另一个相关限制是目标函数需要_二阶可微_。虽然这似乎不是一个大的限制,但需要注意的是,许多常见的神经网络架构使用ReLU激活函数,其二阶导数为零。
相关的问题是高阶导数在遍历参数空间时往往更快地变化,使它们更容易受到损失曲面中高频噪声的影响。
拟牛顿法仍然是一个非常活跃的研究课题,并且因此已经提出了许多扩展方法,可以在特定环境中缓解其中一些问题。例如,通过仅存储可用于近似海森矩阵的低维向量,可以规避内存需求问题。然而,这些困难说明了在应用BFGS等方法时经常出现的问题。
17.5 逆梯度
作为解决上述问题的第一步,我们将考虑所谓的“逆梯度”(Inverse Gradients,IGs)。这些方法实际上使用了雅可比矩阵的逆,但由于计算链的末尾总是有一个标量损失,这会导致一个梯度向量。不幸的是,它们也带来了一系列自己的问题,这就是为什么它们只代表了一个中间步骤(我们稍后会以一种更实际的形式重新考虑它们)。
我们不再考虑标量 ,而是考虑一个通用的、可能非标量的函数 的优化问题。这个函数在后面通常是物理模拟器 ,但为了保持通用和可读性,我们现在称之为 。这个设置意味着一个逆问题:对于 ,我们希望找到一个给定目标 的 。我们定义:
作为IG更新。在这里,雅可比矩阵类似于上述GD更新的反函数,以一阶精度编码了输入必须如何改变才能获得输出中的小变化。关键步骤是反演,当然需要雅可比矩阵可逆。这是一个与海森矩阵反演类似的问题,我们将在下面重新讨论这个问题。然而,如果我们可以反演雅可比矩阵,这将具有一些非常好的性质。
请注意,这里不是使用学习率,而是步长由期望的输出值的增加或减少确定。因此,我们需要选择一个而不是,但实际上扮演着相同的角色:它控制优化的步长。在最简单的情况下,我们可以通过计算出它作为朝向真实值的一步。这个将在以下方程中频繁出现,并使它们乍一看看起来与上述方程非常不同。
单位
IGs随着反导数的变化而变化。因此更新的单位与参数的单位相同,无需任意学习率: 乘以 的单位为 。
函数敏感性
它们在归一化方面也没有问题,因为上述示例中的参数更新从现在按比例缩放为。因此,敏感函数接收到小的更新,而不敏感的函数接收到大的(或爆炸性的)更新。
最优附近收敛和函数组合
与牛顿法类似,IG方法在接近最优点时表现出与GD相反的行为:它们产生的更新仍然推进优化过程,通常有利于收敛。
此外,IG方法在函数组合方面具有一致性。的变化量为,的近似变化量为。中间空间的变化与它们各自的依赖关系无关,至少在一阶导数的情况下是独立的。因此,在反向传播期间,这些空间的变化可以在所有梯度被计算之前进行估计。
请注意,即使是具有逆Hessian矩阵的牛顿法也没有完全做到这一点。关键在于,如果Jacobian矩阵是可逆的,我们将直接获得给定层的正确缩放方向,而无需像逆Hessian矩阵那样使用辅助量。
依赖于逆 Jacobian
目前为止还不错。上述特性显然是有优势的,但不幸的是,IGs需要雅可比矩阵的逆。它仅在雅可比矩阵是方阵时有明确定义,这意味着对于输入和输出维度相同的函数。然而,在优化中,输入通常是高维的,而输出是标量目标函数。类似于拟牛顿方法的海森矩阵,即使是方阵,它也可能不可逆。
因此,我们现在考虑到逆梯度是逆函数的线性化,同时保留相同的优点,使用逆函数可以提供额外的优势。
到目前为止一切顺利。上述性质明显具有优势, 但不幸的是, IG 需要 Jacobian 的逆 。它仅对方 Jacobian 有意义, 这意味着对于输入和输出维度相等的函数 。然而, 在优化中, 输入通常是高维的, 而输出是一个标量目标函数。并且, 与拟牛顿法的海森矩阵 somewhat 类似, 即使 是方的,它也可能不可逆。
因此, 我们现在考虑逆梯度是逆函数的线性化的事实, 并且展示使用逆函数提供了额外的优势, 同时保留相同的好处。
17.6 逆模拟器
到目前为止,我们已经讨论了现有方法的问题,而在表现更好的方法中,如牛顿法和IGs,一个共同的主题是常规梯度是不够的。我们需要以某种形式的“反转”来解决它的问题,以达到尺度不变性。在进入神经网络训练和执行这种反转的数值方法的细节之前,我们将考虑另一个“特殊”情况,这将进一步说明反转的必要性:如果我们可以利用一个“逆向模拟器”,同样可以解决梯度下降法中的许多固有问题。它实际上代表了计算物理模拟部分更新步骤的理想设置。
设为一种正向模拟,表示其逆运算。与之前的雅可比矩阵或海森矩阵的求逆不同,表示对的所有函数进行完全逆运算。
尝试在从顶部开始的最小化问题中使用反演求解器,有点令人惊讶的是,这使得整个最小化问题变得过时(至少对于考虑具有一个对的单个情况而言)。我们只需要评估来解决反问题并获得。由于我们计划很快恢复NN和更复杂的情况,因此假设我们仍然处理一组目标和非明显的解。一个例子可能是,我们正在寻找一个,它产生多个目标,并且在意义下具有最小的失真。
现在,我们可以使用逆物理模拟器来迭代更新当前近似解,而不是仅仅评估一次以获得解。我们将这个更新称为。
同时,使用一个基于初始解猜测的条件化的局部逆也是一个好主意。由于可能存在导致非常相似的不同空间位置,我们希望找到最接近当前猜测的位置。这对于在多模态设置中获得良好的解非常重要,我们希望避免解流形由一组非常分散的点组成。
借助这些改变,我们可以构建一个优化问题,其中优化的当前状态 , ,使用 进行更新。
这里在空间中的步长可以是完整距离或其一部分,与IG的步长保持一致。当应用更新时,尽管是一个可能高度非线性的函数,它将产生。请注意,等式{eq}PG-def中的有效地抵消,以给出关于的步长。然而,这种表示法可以显示与等式{eq}IG-def中的IG步骤的相似之处。
更新给出了第一个迭代方法,它利用了的所有信息,例如高阶项。
17.7 总结
由于缩放问题,使用普通梯度下降方法得到的更新存在令人惊讶的缺陷。经典的基于反演的方法,如IG和牛顿法,通过反演模拟器的更新构造()消除了其中的一些缺陷,其中包括最高阶的项。可以看作是改进(反演)更新步骤的“理想”设置。它正确地获取了上述所有方面:单位、函数灵敏度、组合和接近最优值的收敛性,并提供了一个“尺度不变”的更新。这是以需要表达式和局部反演求解器的离散化为代价的。
与牛顿法和IG的二阶和一阶近似相比,它可以潜在地考虑高度非线性的影响。由于反演模拟器的构造可能很困难,以下各节的主要目标是说明包含所有高阶信息可以获得多大收益。请注意,所有三种方法都成功地通过反演包括了搜索方向的重新缩放,与先前讨论的GD训练相反。尽管所有这些方法都代表不同形式的可微物理,但在将改进的更新包含在NN训练过程中之前,我们将讨论一些附加的理论方面,并用实际例子说明这些方法之间的差异。
17.8 深入了解逆向模拟器
我们将现在更详细地推导和讨论的更新。物理过程可以被描述为状态空间中的轨迹,其中每个点代表系统的一种可能配置。模拟器通常接受一个这样的状态空间向量,并在另一个时间计算一个新的向量。因此,模拟器的雅可比矩阵必然是方阵。只要物理过程不“销毁”信息,雅可比矩阵就是非奇异的。事实上,人们相信我们宇宙中的信息不能被销毁,因此只要我们对状态有完美的知识,任何物理过程理论上都可以被反演。因此,可以合理地期望在许多情况下可以制定。
根据上述描述计算的更新步骤还具有一些良好的理论性质,例如,只要始终收敛到固定目标,优化就会收敛。有关相应证明的详细信息可参见{cite}holl2021pg。
17.8.1 微积分基本定理
为更清晰地说明非线性情况下的优势,我们应用基本定理来重新表达上述比率。这给出, 这里积分内的表达式是局部梯度,我们假设它在 和 之间的所有点都存在。局部梯度沿着连接更新前状态和更新后状态的路径进行平均。因此,整个表达式等于 在当前 和下一次优化步骤的估计值 之间的平均梯度。这实际上相当于通过计算可以考虑 的非线性性的更新来“平滑”优化的目标景观。
通过将积分替换为沿着连接 和 的任何可微路径的路径积分,并将局部梯度替换为沿路径方向的局部梯度,这些方程自然地推广到更高的维度。
17.8.2 全局和局部逆模拟器
设是一个具有方阵雅可比矩阵的函数,。只有双射的才定义了一个全局反函数。如果反函数存在,则它可以找到任何,使得。我
们在实践中通常不直接使用这个“完美”的反函数,而是使用一个局部反函数,它是在点上条件的,并且相应地与有关。这个局部反函数更容易获得,因为它只需要在给定的附近存在,而不是对于所有的。对于通用的存在,需要是全局可逆的。
相比之下,局部反函数只需要在附近存在并且准确即可。如果全局反函数存在,则局部反函数逼近它,并在时完全匹配它。更正式地,。即使全局反函数不存在,局部反函数也可以存在。
例如,非单射函数可以通过选择最接近的,使得来反转。例如,考虑。它没有全局反函数,因为每个存在两个解()。然而,我们可以通过选择最接近的解从一个初始猜测中轻松构造一个局部反函数。对于可微函数,只要雅可比矩阵是非奇异的,局部反函数就有保证存在,这是由于反函数定理保证了这一点。这是因为反雅可比矩阵本身就是一个局部反函数,尽管是一阶的,而不是最准确的反函数。
即使雅可比矩阵是奇异的(因为函数不是单射的、混沌的或嘈杂的),我们通常也可以找到良好的局部反函数。
17.8.3 时间反转
模拟器的逆函数通常是时间反演的物理过程。在某些情况下,将正向模拟器的时间轴反转,即,可以得到一个足够全局的逆模拟器。除非模拟器在实践中破坏了信息,例如由于累积的数值误差或者刚性线性系统,否则这种方法可以作为逆模拟的起点,或者用于构建一个“局部”的逆模拟。
然而,模拟器本身需要具有足够的准确性才能提供正确的估计。对于更复杂的情况,例如在多个时间步骤中进行的流体模拟,{doc}overview-ns-forw中使用的一阶和二阶方案是不够的。
17.8.4 集成损失函数
自从引入IGs以来,我们只考虑了一个具有输出的模拟器。现在我们可以重新引入损失函数。与之前一样,我们考虑具有标量目标函数的最小化问题,该函数取决于可逆模拟器的结果。在方程(1)中,我们引入了逆梯度(IG)更新,当包括损失函数时,它给出。
这里,表示在损失方面要采取的步骤。通过应用链式法则,并将IG 替换为方程(2)中逆物理模拟器的更新,我们得到了一阶近似:
这些方程表明,方程{eq}PG-def在一阶精度上等于上面一节中的IG,但包含非线性项,即。更新的准确性取决于逆函数的保真度。
我们可以使用局部梯度定义局部逆误差的上限。
在最坏的情况下,我们可以回退到常规梯度。此外,我们将对的步骤转化为空间中的步骤:。然而,这并没有规定计算的唯一方法,因为导数作为行向量的右逆几乎没有对施加限制。
相反,我们使用方程(见引用{eq}quasi-newton-update)中的牛顿步骤来确定,其中控制着优化步骤的步长。在接下来的代码示例之后,我们将结合介绍神经网络的内容详细解释这一点。
前面的部分对不同优化方法的优缺点进行了许多评论。接下来,我们将通过一个实际例子展示这些特性实际上产生了多大的差异。
18.1 问题描述
我们将考虑一个非常简单的设置,以清楚地说明发生了什么:我们有一个二维输入空间,一个同样具有两个维度的模拟“物理模型”,以及一个标量损失,即,,以及。向量的分量用表示,并且为了与Python数组保持同步,索引从0开始。
具体而言,我们将使用以下和:
\quad \mathbf{y}(\mathbf{x}) = \mathbf{y}(x_0, x_1) = \begin{bmatrix} x_0 \ x_1^2 \end{bmatrix}
即 仅对其输入的第二个分量进行平方, 表示一个简单的平方 损失。作为一些示例优化的起点,我们将使用 \mathbf{x} = \begin{bmatrix} 3 \ 3 \end{bmatrix} 作为解决以下简单最小化问题的初始猜测:。
对于我们人类来说, 是正确的答案,但让我们看看前面讨论的不同优化算法如何快速找到该解。
18.2 三个空间
为了理解以下示例,重要的是要记住我们在这里处理的是三个“空间”之间的映射:、和。常规前向传递通过将映射到,而对于优化,我们需要将中的值和变化与中的位置相关联。在这样做的同时,有趣的是看看在寻找的正确位置时,它是如何影响到在中形成的位置。
18.3 实现
在这个例子中,我们将使用JAX框架,它是一个有效地处理可微函数的良好选择。JAX还有一个很好的numpy封装,实现了大部分numpy的函数。下面我们将使用这个封装作为np,而将原始的numpy作为onp。
import jax
import jax.numpy as np
import numpy as onp
我们将首先定义和函数,以及一个调用L和y的复合函数fun。对于许多JAX操作,拥有一个单一的本地Python函数是必要的。
# "physics" function y
def physics_y(x):
return np.array( [x[0], x[1]*x[1]] )
# simple L2 loss
def loss_y(y):
#return y[0]*y[0] + y[1]*y[1] # "manual version"
return np.sum( np.square(y) )
# composite function with L & y , evaluating the loss for x
def loss_x(x):
return loss_y(physics_y(x))
x = np.asarray([3,3], dtype=np.float32)
print("Starting point x = "+format(x) +"\n")
print("Some test calls of the functions we defined so far, from top to bottom, y, manual L(y), L(y):")
physics_y(x) , loss_y( physics_y(x) ), loss_x(x)
Starting point x = [3. 3.]
Some test calls of the functions we defined so far, from top to bottom, y, manual L(y), L(y):
现在我们可以通过jax.grad来评估我们函数的导数。例如,jax.grad(loss_y)(physics_y(x))评估了雅可比矩阵。下面的代码单元格评估了这个雅可比矩阵及其几个变体,并对的逆雅可比矩阵进行了一次合理性检查。
# this works:
print("Jacobian L(y): " + format(jax.grad(loss_y)(physics_y(x))) +"\n")
# the following would give an error as y (and hence physics_y) is not scalar
#jax.grad(physics_y)(x)
# computing the jacobian of y is a valid operation:
J = jax.jacobian(physics_y)(x)
print( "Jacobian y(x): \n" + format(J) )
# the code below also gives error, JAX grad needs a single function object
#jax.grad( loss_y(physics_y) )(x)
print( "\nSanity check with inverse Jacobian of y, this should give x again: " + format(np.linalg.solve(J, np.matmul(J,x) )) +"\n")
# instead use composite 'fun' from above
print("Gradient for full L(x): " + format( jax.grad(loss_x)(x) ) +"\n")
Jacobian L(y): [ 6. 18.]
Jacobian y(x):
[[1. 0.]
[0. 6.]]
Sanity check with inverse Jacobian of y, this should give x again: [3. 3.]
Gradient for full L(x): [ 6. 108.]
最后一行值得仔细观察:在这里,我们打印初始位置的梯度。虽然我们知道我们应该沿对角线朝向原点移动(零向量是最小化器),但是这个梯度并不是非常对角线 - 它在方向上有一个强烈的主导分量,其值为108。
让我们看看不同的方法如何应对这种情况。我们将比较以下三种方法:
- 一阶方法梯度下降(即常规的、非随机的、“最陡峭的梯度下降”)
- 牛顿法作为二阶方法的代表,
- 逆模拟器中的标度不变更新。
18.4 梯度下降
对于梯度下降法,在我们的设置中,基于简单梯度的更新方程(见公式{eq}GD-update)给出了如下关于 的更新步骤:
其中 表示步长参数。
让我们从开始使用梯度下降进行优化,并使用更新我们的解十次:
x = np.asarray([3.,3.])
eta = 0.01
historyGD = [x]; updatesGD = []
for i in range(10):
G = jax.grad(loss_x)(x)
x += -eta * G
historyGD.append(x); updatesGD.append(G)
print( "GD iter %d: "%i + format(x) )
GD iter 0: [2.94 1.9200001]
GD iter 1: [2.8812 1.6368846]
GD iter 2: [2.823576 1.4614503]
GD iter 3: [2.7671044 1.3365935]
GD iter 4: [2.7117622 1.2410815]
GD iter 5: [2.657527 1.1646168]
GD iter 6: [2.6043763 1.1014326]
GD iter 7: [2.5522888 1.0479842]
GD iter 8: [2.501243 1.0019454]
GD iter 9: [2.4512184 0.96171147]
在这里,我们已经打印出了中的结果位置,并且它们似乎在下降,即向正确的方向移动。最后一个点距离原点还有2.63的相当距离。
让我们来看一下迭代过程中的进展(演化已存储在上面的history列表中)。蓝色点表示GD迭代中中的位置,目标在原点处用细黑十字表示。
import matplotlib.pyplot as plt
axes = plt.figure(figsize=(4, 4), dpi=100).gca()
historyGD = onp.asarray(historyGD)
updatesGD = onp.asarray(updatesGD) # for later
axes.scatter(historyGD[:,0], historyGD[:,1], lw=0.5, color='#1F77B4', label='GD')
axes.scatter([0], [0], lw=0.25, color='black', marker='x') # target at 0,0
axes.set_xlabel('x0'); axes.set_ylabel('x1'); axes.legend()
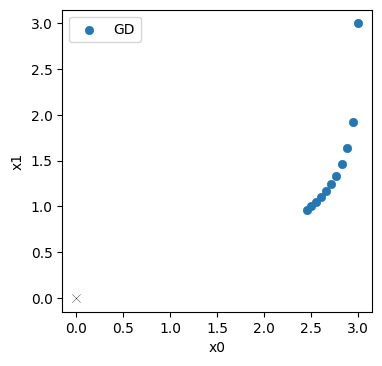
毫不意外的是:初始步骤大部分沿着向下移动(在右上角),之后的更新向原点弯曲。但它们并没有走得很远。到达左下角的解仍然相当遥远。
18.5 牛顿法
对于牛顿法, 更新步骤给出 因此,除了与GD相同的梯度外,我们现在需要评估和求Hessian矩阵的逆。
在JAX中,这非常简单:我们可以调用jax.jacobian两次,然后使用JAX版本的linalg.inv来反转得到的矩阵。
对于使用牛顿法的优化,我们将使用更大的步长。对于这个例子和下一个例子,我们选择了步长,使得第一次更新步骤的大小大致与GD的大小相同。通过这种方式,我们可以相对于彼此比较所有三种方法的轨迹。请注意,这绝不意味着这里的方法的稳定性或上限的比较。稳定性和的上限是分开的主题。这里我们专注于收敛性质。
在下一个单元格中,我们从相同的初始猜测开始应用十次Newton更新:
x = np.asarray([3.,3.])
eta = 1./3.
historyNt = [x]; updatesNt = []
Gx = jax.grad(loss_x)
Hx = jax.jacobian(jax.jacobian(loss_x))
for i in range(10):
g = Gx(x)
h = Hx(x)
hinv = np.linalg.inv(h)
x += -eta * np.matmul( hinv , g )
historyNt.append(x); updatesNt.append( np.matmul( hinv , g) )
print( "Newton iter %d: "%i + format(x) )
Newton iter 0: [2. 2.6666667]
Newton iter 1: [1.3333333 2.3703704]
Newton iter 2: [0.88888884 2.1069958 ]
Newton iter 3: [0.59259254 1.8728852 ]
Newton iter 4: [0.39506167 1.6647868 ]
Newton iter 5: [0.26337445 1.4798105 ]
Newton iter 6: [0.17558296 1.315387 ]
Newton iter 7: [0.1170553 1.1692328]
Newton iter 8: [0.07803687 1.0393181 ]
Newton iter 9: [0.05202458 0.92383826]
最后一行已经表明:牛顿法的效果要好得多。最后一个点到原点的距离只有0.925(相比于梯度下降法的2.63)。
下面,我们将牛顿法的轨迹以橙色绘制在梯度下降法的蓝色版本旁边。
axes = plt.figure(figsize=(4, 4), dpi=100).gca()
historyNt = onp.asarray(historyNt)
updatesNt = onp.asarray(updatesNt)
axes.scatter(historyGD[:,0], historyGD[:,1], lw=0.5, color='#1F77B4', label='GD')
axes.scatter(historyNt[:,0], historyNt[:,1], lw=0.5, color='#FF7F0E', label='Newton')
axes.scatter([0], [0], lw=0.25, color='black', marker='x') # target at 0,0
axes.set_xlabel('x0'); axes.set_ylabel('x1'); axes.legend()
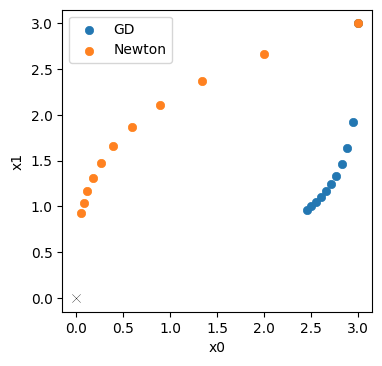
并不完全令人惊讶:对于这个简单的例子,我们可以可靠地评估Hessian矩阵,并且牛顿法从二阶信息中获益。它的轨迹更加沿对角线(这将是理想的、通往解的最短路径),并且不像梯度下降法那样减速明显。
18.6 逆模拟器
现在我们还使用了的解析逆来进行优化。它代表了我们之前章节中的逆模拟器:,用于计算下面所示的尺度不变更新(记为PG)。稍微预告一下下一节,我们将使用牛顿步骤来更新,并将其与逆物理函数结合起来得到整体更新。这给出了一个更新步骤:
下面,我们定义了我们的逆函数physics_y_inv_analytic,然后使用PG更新方法对其进行了十步的优化评估:
x = np.asarray([3.,3.])
eta = 0.3
historyPG = [x]; historyPGy = []; updatesPG = []
def physics_y_inv(y):
return np.array( [y[0], np.power(y[1],0.5)] )
Gy = jax.grad(loss_y)
Hy = jax.jacobian(jax.jacobian(loss_y))
for i in range(10):
# Newton step for L(y)
zForw = physics_y(x)
g = Gy(zForw)
h = Hy(zForw)
hinv = np.linalg.inv(h)
# step in y space
zBack = zForw -eta * np.matmul( hinv , g)
historyPGy.append(zBack)
# "inverse physics" step via y-inverse
x = physics_y_inv(zBack)
historyPG.append(x)
updatesPG.append( historyPG[-2] - historyPG[-1] )
print( "PG iter %d: "%i + format(x) )
PG iter 0: [2.1 2.5099802]
PG iter 1: [1.4699999 2.1000001]
PG iter 2: [1.0289999 1.7569861]
PG iter 3: [0.72029996 1.47 ]
PG iter 4: [0.50421 1.2298902]
PG iter 5: [0.352947 1.029 ]
PG iter 6: [0.24706289 0.86092323]
PG iter 7: [0.17294402 0.7203 ]
PG iter 8: [0.12106082 0.60264623]
PG iter 9: [0.08474258 0.50421 ]
现在我们得到了作为最终位置,仅有0.51的距离!这显然比牛顿法和梯度下降法都要好。
让我们直接可视化一下与牛顿法(橙色)和梯度下降法(蓝色)相比,PGs(红色)的效果如何。
historyPG = onp.asarray(historyPG)
updatesPG = onp.asarray(updatesPG)
axes = plt.figure(figsize=(4, 4), dpi=100).gca()
axes.scatter(historyGD[:,0], historyGD[:,1], lw=0.5, color='#1F77B4', label='GD')
axes.scatter(historyNt[:,0], historyNt[:,1], lw=0.5, color='#FF7F0E', label='Newton')
axes.scatter(historyPG[:,0], historyPG[:,1], lw=0.5, color='#D62728', label='PG')
axes.scatter([0], [0], lw=0.25, color='black', marker='x') # target at 0,0
axes.set_xlabel('x0'); axes.set_ylabel('x1'); axes.legend()
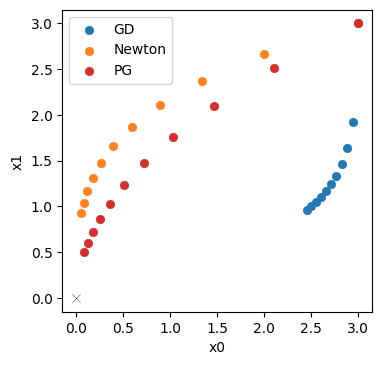
这说明反向模拟器变种红色的PG,甚至比橙色的牛顿法更好。它产生了一条与理想“对角线”轨迹更为一致的轨迹,并且其最终状态更接近原点。这里的一个关键因素是的反函数,它提供了比牛顿法的二阶近似更高阶的项。这改善了优化的尺度不变性。尽管问题很简单,牛顿法在找到正确的搜索方向方面存在问题。另一方面,反向模拟器更新利用了更高阶的信息,为优化提供了改进的方向。
这种差异也体现在每种方法的第一次更新步骤中:下面我们测量它与对角线的对齐程度。
def mag(x):
return np.sqrt(np.sum(np.square(x)))
def one_len(x):
return np.dot( x/mag(x), np.array([1,1]))
print("Diagonal lengths (larger is better): GD %f, Nt %f, PG %f " %
(one_len(updatesGD[0]) , one_len(updatesNt[0]) , one_len(updatesPG[0])) )
Diagonal lengths (larger is better): GD 1.053930, Nt 1.264911, PG 1.356443
PG 的最大值 1.356 证实了我们上面所看到的:PG 梯度是最接近从起点到原点的对角线方向的梯度。
18.7 y 空间
为了理解这些方法的行为和差异,重要的是要记住,我们不是在处理将映射到的黑盒子,而是在处理中间的空间。在我们的情况下,我们只有一个空间,但对于深度学习设置,我们可能有许多潜在空间,我们对其具有一定控制权。我们很快就会回到神经网络,但现在让我们专注于。
首先要注意的是,对于PG,我们显式地从映射到,然后继续映射到。因此,我们已经在空间中获得了轨迹,并且不巧的是,我们已经将其存储在上面的historyPGy列表中。
让我们直接看看逆模拟器在空间中做了什么:
historyPGy = onp.asarray(historyPGy)
axes = plt.figure(figsize=(4, 4), dpi=100).gca()
axes.set_title('y space')
axes.scatter(historyPGy[:,0], historyPGy[:,1], lw=0.5, color='#D62728', marker='*', label='PG')
axes.scatter([0], [0], lw=0.25, color='black', marker='*')
axes.set_xlabel('z0'); axes.set_ylabel('z1'); axes.legend()
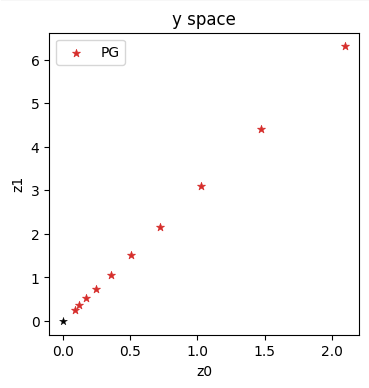
在这个变种中,我们在空间中采取明确的步骤,这些步骤沿着一条直对角线向原点前进(这也是空间中的解)。
有趣的是,无论是梯度下降法(GD)还是牛顿法都无法提供关于中间空间(如空间)进展的信息。
对于梯度下降法,我们正在连接雅可比矩阵,因此我们在局部应该沿着降低损失的方向移动。然而,的位置受到的影响,因此在我们确定在空间的具体点之前,我们不知道最终会到达哪里(对于神经网络来说,一般情况下,在进行梯度下降更新后,我们不知道在哪些潜在空间点上结束,直到我们实际计算出所有更新的权重)。
更具体地说,对于梯度下降法,我们有一个更新,这意味着我们在空间中到达。使用进行泰勒展开得到:
而显然与我们在直接优化时使用的不同。
牛顿法也不太好:我们首先计算像GD一样的一阶导数,然后计算完整过程的Hessian的二阶导数。但由于两者都是近似值,因此更新步骤产生的实际中间状态在评估完整链之前是未知的。在{doc}physgrad中,牛顿法的函数组合一致性段落中,Hessian的平方项已经表明了这种依赖关系。
对于逆模拟器,我们没有这个问题:它们可以直接将空间中的点映射到空间中。因此,我们知道我们在空间中开始的位置,因为这个位置对于评估反演是至关重要的。
在本节的简单设置中,我们只有一个潜在空间,并且我们已经在优化过程中存储了所有的空间中的值(在history列表中)。因此,现在我们可以返回并重新评估physics_y以获取空间中的位置。
x = np.asarray([3.,3.])
eta = 0.01
historyGDy = []
historyNty = []
for i in range(1,10):
historyGDy.append(physics_y(historyGD[i]))
historyNty.append(physics_y(historyNt[i]))
historyGDy = onp.asarray(historyGDy)
historyNty = onp.asarray(historyNty)
axes = plt.figure(figsize=(4, 4), dpi=100).gca()
axes.set_title('y space')
axes.scatter(historyGDy[:,0], historyGDy[:,1], lw=0.5, marker='*', color='#1F77B4', label='GD')
axes.scatter(historyNty[:,0], historyNty[:,1], lw=0.5, marker='*', color='#FF7F0E', label='Newton')
axes.scatter(historyPGy[:,0], historyPGy[:,1], lw=0.5, marker='*', color='#D62728', label='PG')
axes.scatter([0], [0], lw=0.25, color='black', marker='*')
axes.set_xlabel('z0'); axes.set_ylabel('z1'); axes.legend()
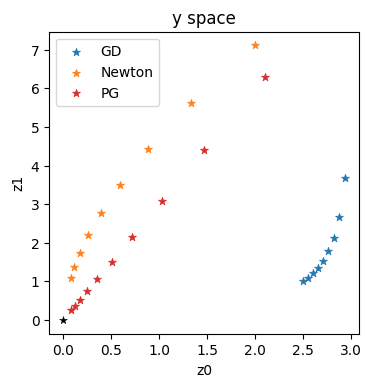
这些轨迹证实了前几节中所概述的直觉:蓝色的梯度下降在方向上给出了一个非常次优的轨迹。牛顿法(橙色)表现更好,但仍然明显弯曲。它不能很好地近似这个例子的高阶项。这与使用逆模拟器进行优化的直线和对角线红色轨迹形成对比。
当中间空间不仅仅是抽象的潜在空间,而是具有实际物理意义时,其行为变得尤为重要。
18.8 结论
尽管简单, 但这个例子已经显示出梯度下降、牛顿法和使用逆模拟器之间令人惊讶的大差异。
本节的主要要点如下。
- GD 很容易产生“不平衡”的更新, 并陷入僵局。
- 牛顿法做得更好, 但远非最优。
- 尽管只应用了部分 (我们上面仍然对 使用了牛顿法), 但逆模拟器的高阶信息优于两者。
- 此外,方法(一般来说是优化器的选择)对潜空间的研究进展也有很大影响,如上文𝑦 的情况所示。
在接下来的章节中, 我们可以基于这些观察结果, 通过可逆物理模型使用 PG 进行神经网络训练。
18.9 近似求逆
如果像上面的physics_y_inv_analytic这样的解析逆函数不容易得到,我们实际上可以采用优化方案,如牛顿法或BFGS,以数值方式获得局部逆函数。这是一个与不同优化方法的比较无关的主题,但可以基于上面的逆模拟器变体进行简单的说明。
下面,我们将使用scipy中的BFGS变体fmin_l_bfgs_b来计算逆函数。这并不是非常复杂,但我们将直接使用numpy和scipy,这使得代码有点混乱。
def physics_y_inv_opt(target_y, x_ini):
# a bit ugly, we switch to pure scipy here inside each iteration for BFGS
import numpy as np
from scipy.optimize import fmin_l_bfgs_b
target_y = onp.array(target_y)
x_ini = onp.array(x_ini)
def physics_y_opt(x,target_y=[2,2]):
y = onp.array( [x[0], x[1]*x[1]] ) # we cant use physics_y from JAX here
ret = onp.sum( onp.square(y-target_y) )
return ret
ret = fmin_l_bfgs_b(lambda x: physics_y_opt(x,target_y), x_ini, approx_grad=True )
#print( ret ) # return full BFGS details
return ret[0]
print("BFGS optimization test run, find x such that y=[2,2]:")
physics_y_inv_opt([2,2], [3,3])
BFGS optimization test run, find x such that y=[2,2]:
array([2.00000003, 1.41421353])
尽管如此,我们现在可以使用这个数值反转的 函数来进行逆模拟器优化。除了调用 physics_y_inv_opt 函数外,其余代码保持不变。
x = np.asarray([3.,3.])
eta = 0.3
history = [x]; updates = []
Gy = jax.grad(loss_y)
Hy = jax.jacobian(jax.jacobian(loss_y))
for i in range(10):
# same as before, Newton step for L(y)
y = physics_y(x)
g = Gy(y)
y += -eta * np.matmul( np.linalg.inv( Hy(y) ) , g)
# optimize for inverse physics, assuming we dont have access to an inverse for physics_y
x = physics_y_inv_opt(y,x)
history.append(x)
updates.append( history[-2] - history[-1] )
print( "PG iter %d: "%i + format(x) )
PG iter 0: [2.09999967 2.50998022]
PG iter 1: [1.46999859 2.10000011]
PG iter 2: [1.02899871 1.75698602]
PG iter 3: [0.72029824 1.4699998 ]
PG iter 4: [0.50420733 1.22988982]
PG iter 5: [0.35294448 1.02899957]
PG iter 6: [0.24705997 0.86092355]
PG iter 7: [0.17294205 0.72030026]
PG iter 8: [0.12106103 0.60264817]
PG iter 9: [0.08474171 0.50421247]
这证实了近似求逆的有效性,与上述常规PG版本一致。没有太多意义来绘制这个,因为基本上是一样的,但我们可以测量差异。下面,我们计算了MAE,对于这个简单的例子,结果与我们的浮点精度相当。
historyPGa = onp.asarray(history)
updatesPGa = onp.asarray(updates)
print("MAE difference between analytic PG and approximate inversion: %f" % (np.average(np.abs(historyPGa-historyPG))) )
MAE difference between analytic PG and approximate inversion: 0.000001
18.10 下一步
基于这个代码示例,你可以尝试以下修改:
- 用其他更复杂的函数替换上述简单的 L(y(x)) 函数。
- 用其他优化器替换简单的“常规”梯度下降,例如常用的 DL 优化器,如 AdaGrad、RmsProp 或 Adam。将现有版本与新轨迹进行比较。
前两节的讨论已经暗示了梯度反转是优化和学习的重要步骤。现在我们将把更新步骤整合到神经网络训练中,并详细介绍在之前的代码中已经使用的逆模拟器和牛顿步骤的双向过程。
如Scale-Invariance and Inversion中的 IG 部分所概述的,我们将重点放在下面的逆问题的神经网络求解上。这意味着我们有,我们的目标是训练一个神经网络表示,使得。这是一个比我们之前考虑的可微物理(DP)训练更为受限的设置。另外,由于我们现在的目标是优化算法,我们不会明确地表示DP方法:以下所有的变体都涉及物理模拟器,梯度下降(GD)版本以及其变体(如Adam)都使用DP训练。
需要记住的重要一点是:与前面的部分和{doc}
overview-equations相反,我们的目标是逆问题,因此是网络的输入:。相应地,它输出。
这给出了以下最小化问题,其中表示小批量的索引:
19.1 神经网络训练
为了将方程(24) 中的更新步骤整合到神经网络的训练过程中,我们考虑三个组成部分:神经网络本身、物理模拟器和损失函数。
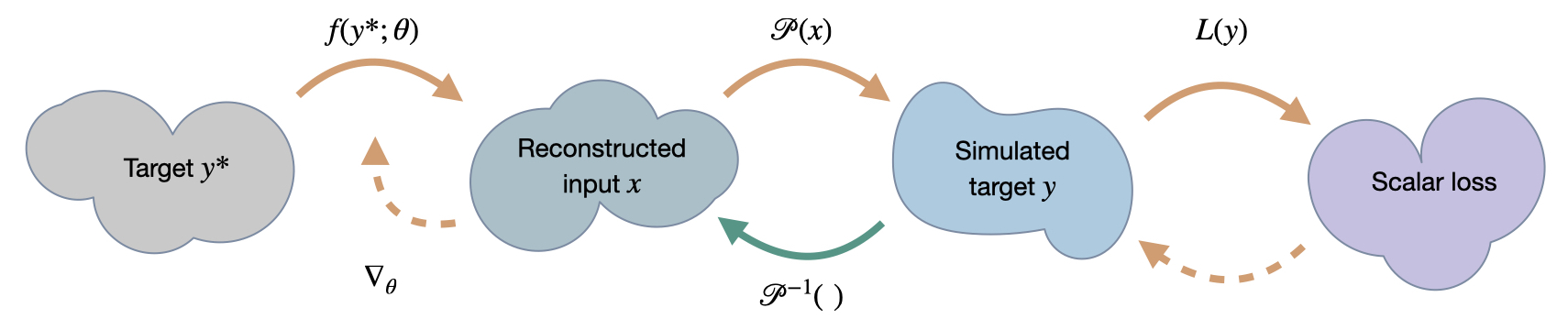
为了将这三个部分结合起来,我们使用以下算法。正如Holl等人在{cite}holl2021pg中介绍的那样,我们将把这个训练过程称为“尺度不变物理”(SIP)训练。
尺度不变物理 (SIP)训练:
为了更新神经网络的权重,我们执行以下更新步骤:
- 给定一组输入,通过前向传播计算神经网络的预测
- 通过前向模拟计算(),并调用(局部)逆模拟器获得步长,其中
- 计算网络损失,例如,其中,并进行牛顿步骤,将视为常数
- 使用梯度下降(或类似Adam的基于梯度下降的优化器)将的变化传播到网络权重,学习率为
该组合优化算法依赖于网络的学习率和上述步长,它影响到。一阶近似下,网络权重的有效学习率为。我们建议将设置为反向模拟器精度允许的最大值。在许多情况下,可以设置,否则应相应调整。这样可以最大限度地利用模拟器的非线性来调整优化方向。
该算法将反向模拟器与传统的神经网络训练方案相结合,以计算准确的高阶更新。这是一个有吸引力的特性,因为我们有一系列强大的神经网络训练方法,这些方法在这种方式下仍然适用。损失函数在神经网络和物理组件之间的处理在这里起着核心作用。

19.2 损失函数
在上述算法中,我们假设了一个损失,并且在没有进一步解释的情况下引入了牛顿步骤来传播逆模拟器步骤到神经网络。下面,我们将更详细地解释和证明这种处理方法。
引入牛顿步骤的核心原因是提高损失导数的准确性。与常规的牛顿方法或方程{eq}quasi-newton-update中的拟牛顿方法不同,我们不需要完整系统的Hessian矩阵。相反,Hessian矩阵仅对需要。这使得牛顿方法再次具有吸引力。更好的是,对于许多典型的函数,牛顿更新的解析形式是已知的。
例如,考虑最常见的监督学习目标函数 ,如上文所述。其中 表示预测值, 表示目标值。我们有 和 。使用方程 {eq}quasi-newton-update,我们得到 ,可以立即计算,无需评估任何额外的 Hessian 矩阵。
确定 后,可以使用逆模拟器 将梯度反向传播到 ,例如一个较早的时间。我们已经在 {doc}physgrad-comparison 中使用了这种损失的牛顿步骤和 PDE 的逆模拟器的组合。
这里的上的损失作为一个“代理”来嵌入逆模拟器的更新到网络训练流程中。它不应与传统的空间中的监督损失混淆。由于对预测的依赖性,它不会将空间中的多个解模式进行平均。为了证明这一点,考虑使用GD作为逆模拟的求解器的情况。然后,总损失纯粹在空间中定义,简化为常规的一阶优化。
因此,总结起来,我们在的损失中使用一个平凡的牛顿步骤,并在上使用一个代理损失,将逆物理和神经网络的计算图连接起来进行反向传播。下图可视化了不同的步骤。

19.3 迭代和时间依赖性
以上过程描述了优化使单个预测的神经网络的方法。这适用于在给出时系统状态的重构,或者估计一个在时满足特定条件的最佳初始状态。
然而,SIP方法也可以应用于涉及多个目标和不同时间点的多个网络交互的更复杂设置。这种情况常出现在控制任务中,其中网络在每个时间步骤诱导小力以达到时的特定物理状态。它也出现在校正任务中,网络试图通过在每个时间步骤执行校正来提高模拟质量。
在这些情况下,上述过程(损失的牛顿步骤,物理的逆模拟器步骤,神经网络的梯度下降)会迭代重复,例如在不同时间步骤中进行,导致中一系列加法项。 这通常使学习任务更加困难,因为我们需要反复反向传播物理求解器和神经网络的迭代,但上述SIP算法就像常规的梯度下降训练一样适用于这些情况。
19.4 SIP 训练实例
让我们通过一个示例来说明SIP训练的收敛行为以及它如何取决于的特性{cite}holl2021pg。我们考虑合成的二维函数:
其中表示旋转矩阵。参数和允许我们连续地改变系统的特性。的值决定了的条件,大的表示病态问题,而描述了和的耦合。当时,Hessian矩阵的非对角线元素消失,问题分解为两个独立的问题。
以下是,,的结果损失函数示例,显示了对于的正弦函数和的线性变化的交织:
接下来,我们使用全连接神经网络通过方程{eq}eq:unsupervised-training来反演这个问题。我们将比较使用无鞍牛顿求解器的SIP训练和各种最先进的网络优化器。
为了公平起见,每个优化器都独立选择最佳学习率。当选择时,问题是完美的条件。在这种情况下,所有网络优化器都收敛,Adam略有优势。这在左图中显示:
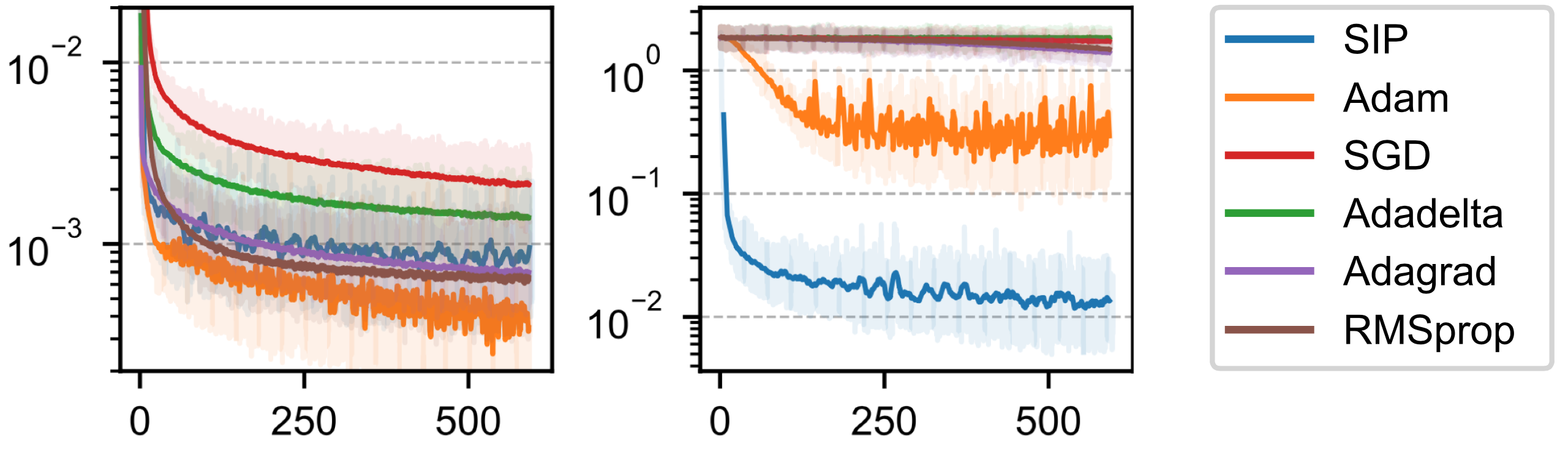
在时,我们有一个相当糟糕的条件情况,只有SIP和Adam成功地对网络进行了显著程度的优化,如右图所示。
请注意,上面的两个图显示了随时间的收敛情况。SIP的相对较慢收敛主要是因为每次迭代所需的时间明显比其他方法长,平均需要的时间是Adam的3倍。虽然Hessian矩阵的评估本质上需要更多的计算,但通过优化计算过程,SIP的每次迭代时间可能会显著减少。
通过增加而保持不变,我们可以展示条件不断影响不同方法的情况,如左图所示。
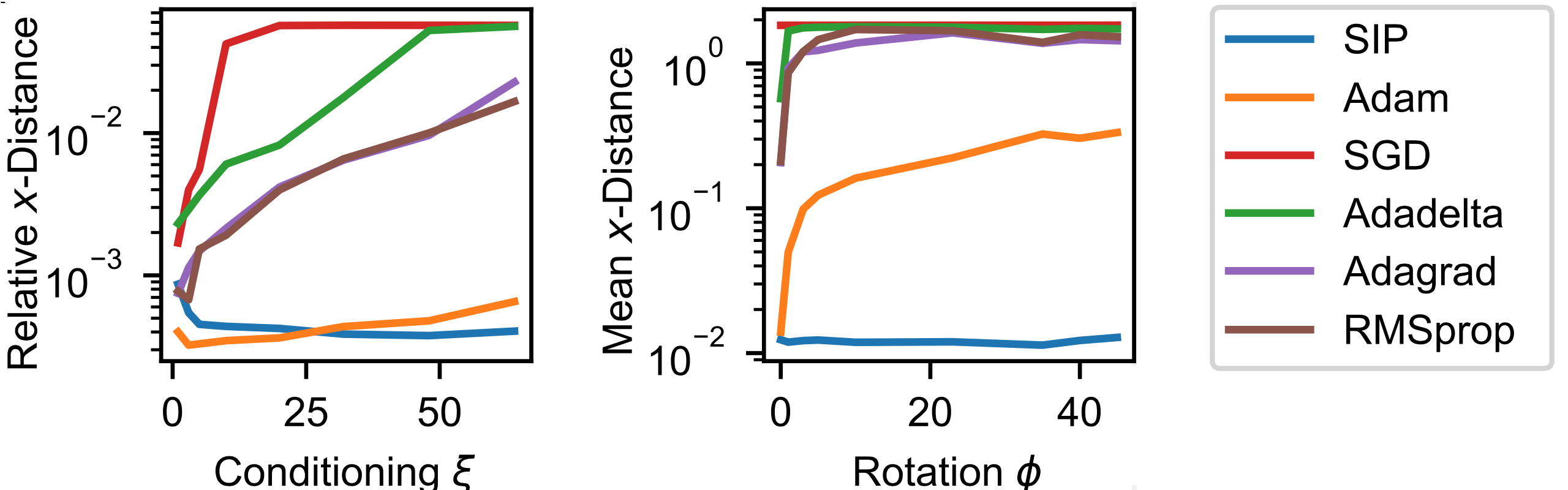
所有传统的网络优化器的准确性都会降低,因为梯度与中的成比例,导致在需要更精确值的方向上变得更长。SIP训练通过使用Hessian矩阵来避免这种情况,反转了缩放行为,并产生与中的平坦方向对齐的更新。这使得SIP训练在广泛的范围内保持相对准确性。即使对于Adam优化器,当变大时准确性也会变差。
通过仅变化,我们可以展示不同组件之间的交织如何影响优化器的行为。{numref}physgrad-sin-add-graphs的右图保持不变,变化。这揭示了Adam如何在病态设置中学习。当和处于不同尺度时,Adam通过对Hessian矩阵进行对角线近似来减小缩放效应,但当参数耦合时,缺少非对角线项阻止了这一点。在这种情况下,其性能下降了一个数量级以上。SIP训练对于耦合参数没有问题,因为其优化更新步骤使用了全秩Hessian矩阵。因此,SIP训练在这个示例设置提出的不同优化问题中产生了最佳结果。

19.5 对 SIP 训练的讨论
虽然我们目前只研究了较小的玩具问题,但我们将推进对SIP训练的讨论。下一章将通过一个更复杂的例子来说明这一点,但由于我们随后将直接切换到一个新的算法,因此下面是一个更好的地方来讨论SIP的性质。
总体而言,SIP训练的尺度不变性使其能够在许多物理问题上以指数级速度找到解决方案,同时保持相对较低的计算成本。当每次求解器评估都执行了足够的网络更新时,可以证明它能够收敛,并且可以证明它在广泛的物理实验中通过单个更新也能够收敛。
19.5.1 局限性
SIP训练可以找到更准确的解,但也有一些需要考虑的注意事项。
首先,需要一个大致尺度不变的物理求解器。在低维度的空间中,牛顿法是一个很好的选择,但在高维空间中需要其他形式的反演。有些方程可以在局部解析反演,但对于复杂问题,可能需要特定领域的知识,或者可以采用数值方法(即将要讨论的内容)。
其次,SIP侧重于对物理部分进行准确的反演,但使用传统的一阶优化器来确定。正如讨论过的,这些求解器在病态环境中表现不佳,这也会影响到SIP在网络输出在非常不同的尺度上的表现。因此,我们应该将反演NN作为目标。
第三,虽然SIP训练通常会导致更准确的解,但在空间中测量,对于损失来说并不总是如此。SIP训练平等地权衡所有示例,而不考虑它们的损失值。这可能是有用的,但在具有过度小或大曲率区域的示例中,会扭曲样本的重要性。在这些情况下,或者当空间中的准确性不重要时,例如在控制任务中,传统的训练方法可能比SIP训练表现更好。
19.5.2 与监督训练的相似之处
有趣的是,SIP训练类似于{doc}supervised中的监督方法。它有效地提供了一种可靠的更新方法,该方法在训练时实时计算。反向模拟器提供所需的反演,可能采用高阶方法,并避免了多模态解的平均化(参见{doc}intro-teaser)。
这是此设置的主要优点之一:预先计算的数据集无法考虑多模态性,因此一旦从输入到参考解的映射不唯一,就会不可避免地导致学习到次优解。同时,这也说明了{doc}diffphys中DP训练的一个困难之处:它产生的梯度没有得到适当的反演,并且很难通过预处理可靠地进行归一化。因此,在训练时可能会出现{doc}physgrad中讨论的缩放问题,并相应地给出消失和爆炸梯度。这些问题是本章要解决的问题。
在下一节中,我们将展示一个更复杂的例子,使用来自逆向模拟器的SIP更新来训练基于物理的神经网络,然后解释另一种求解规模问题的替代方法。
现在我们转向一个实际的例子,使用尺度不变物理(SIP)更新来处理更复杂的问题,具体而言,我们将考虑热方程,它提出了一些特别有趣的挑战:可微物理(DP)梯度只是扩散更多,而反演在数值上是具有挑战性的。下面,我们将解释SIP是如何解决前者的,而特殊的求解器可以解决后者的问题。
下面的笔记本提供了通过phiflow进行完整实现的数据生成、运行DP版本和计算改进的SIP更新的方法。
20.1 问题描述
我们考虑一个由热传导方程控制的二维系统。给定在时刻的初始状态,模拟器通过计算出后续时刻的状态。对于,可以精确反演这个系统,但对于较大的,反演过程变得越来越不稳定,因为初始不同的热量水平会随着时间的推移逐渐平均,使原始信息淹没在噪声中。因此,物理学的雅可比矩阵接近奇异。
我们将使用周期边界条件,并在频率空间中计算结果,物理学可以通过进行解析计算,其中表示傅里叶变换向量的第个元素。 在常规的正向模拟中,高频率成分以指数方式衰减。我们需要重新考虑逆模拟器中的这个方面。
总结起来,我们所追求的反演问题可以写成最小化:
20.2 实现
下面,我们将在一个由64x64个单位长度的单元格组成的域上设置。这种扩散水平具有挑战性,会耗散大部分细节,同时保留大尺度结构。
我们将使用phiflow作为默认后端的PyTorch,但是这个示例代码同样可以在TensorFlow上运行(只需在下面切换到phi.tf.flow)。
!pip install --upgrade --quiet phiflow==2.2
#!pip install --upgrade --quiet git+https://github.com/tum-pbs/PhiFlow
from phi.torch.flow import * # switch to TF with "phi.tf.flow"
20.3 数据生成
对于训练,我们通过在域中随机放置4到10个随机大小和形状的“热”矩形来生成。下面的generate_heat_example()函数生成一个完整的小批量(通过shape.batch)的示例位置。这些位置将在后面作为。它们不会传递给求解器,但应该由神经网络进行重构。
def generate_heat_example(*shape, bounds: Box = None):
shape = math.merge_shapes(*shape)
heat_t0 = CenteredGrid(0, extrapolation.PERIODIC, bounds, resolution=shape.spatial)
bounds = heat_t0.bounds
component_counts = math.to_int32(4 + 7 * math.random_uniform(shape.batch))
positions = (math.random_uniform(shape.batch, batch(components=10), channel(vector=shape.spatial.names)) - 0.5) * bounds.size * 0.8 + bounds.size * 0.5
for i in range(10):
position = positions.components[i]
half_size = math.random_uniform(shape.batch, channel(vector=shape.spatial.names)) * 10
strength = math.random_uniform(shape.batch) * math.to_float(i < component_counts)
position = math.clip(position, bounds.lower + half_size, bounds.upper - half_size)
component_box = Cuboid(position, half_size)
component_mask = SoftGeometryMask(component_box)
component_mask = component_mask.at(heat_t0)
heat_t0 += component_mask * strength
return heat_t0
数据是在训练过程中动态生成的,但现在让我们使用phiflow的vis.plot函数来查看两个示例:
vis.plot(generate_heat_example(batch(view_examples=2), spatial(x=64, y=64)));

20.4 可微分物理和梯度下降
到目前为止,这个设置并没有阻止我们使用在{doc}diffphys中描述的常规动态规划(DP)训练方法。
对于这个扩散情况,我们可以以解析方式写出梯度下降更新公式,如下所示:
观察这个表达式,它意味着使用可微分模拟器的梯度下降(GD)将前向物理应用于梯度向量本身。这是令人惊讶的:前向模拟执行扩散,而现在反向传播执行更多的扩散,而不是以某种方式撤消扩散?不幸的是,这是DP的固有且“正确”的行为,它导致更新是稳定的但缺乏高频空间信息。因此,在拟合粗糙结构之后,基于GD的优化方法在这个任务上收敛缓慢,并且在恢复高频细节方面存在严重问题,如下所示。
这不是因为信息本质上缺失,而是因为GD无法充分处理高频细节。
对于下面的实现,我们将简单地使用y = diffuse.fourier(x, 8., 1)进行前向传递,然后类似地计算两个应用了diffuse.fourier( , 8., 1)的场的损失。
20.5 稳定的 SIP 梯度
在本章的背景下,更有趣的是通过逆向模拟器计算得到的改进更新步骤,即SIP更新。与前面的章节一致,我们将称此更新为。
热方程的频率形式可以通过解析求逆,得到。这使我们能够定义更新步骤。
在这里,高频率被指数级的因子所乘,导致数值不稳定性。直接将这个公式应用于梯度时,可能会导致的大幅波动。
请注意,即使在实际空间而非频率空间计算梯度时,这些数值不稳定性也会出现。然而,频率空间使我们更容易量化这些不稳定性。
现在,我们可以利用我们对物理模拟过程的了解来构建一个稳定的逆过程:通过采取概率观点,可以避免数值不稳定性。观察值包含一定量的噪声,其余部分构成信号。对于噪声,我们假设其服从正态分布,其中;对于信号,我们假设其来自于合理的值,以使,其中。有了这个,我们可以使用贝叶斯定理估计一个观察值来自信号的概率,其中我们假设先验。基于这个概率,我们抑制逆物理的放大,从而得到一个稳定的逆过程。
以这种方式计算的梯度保留了尽可能多的高频信息,考虑到存在的噪声。这比任何通用优化方法都具有更快的收敛速度和更精确的解决方案。下面的单元格实现了这种概率方法,其中apply_damping()中的probability_signal包含要抑制的信号部分。inv_diffuse()函数使用它来计算一个稳定的逆扩散过程。
def apply_damping(kernel, inv_kernel, amp, f_uncertainty, log_kernel):
signal_prior = 0.5
expected_amp = 1. * kernel.shape.get_size('x') * inv_kernel # This can be measured
signal_likelihood = math.exp(-0.5 * (abs(amp) / expected_amp) ** 2) * signal_prior # this can be NaN
signal_likelihood = math.where(math.isfinite(signal_likelihood), signal_likelihood, math.zeros_like(signal_likelihood))
noise_likelihood = math.exp(-0.5 * (abs(amp) / f_uncertainty) ** 2) * (1 - signal_prior)
probability_signal = math.divide_no_nan(signal_likelihood, (signal_likelihood + noise_likelihood))
action = math.where((0.5 >= probability_signal) | (probability_signal >= 0.68), 2 * (probability_signal - 0.5), 0.) # 1 sigma required to take action
prob_kernel = math.exp(log_kernel * action)
return prob_kernel, probability_signal
def inv_diffuse(grid: Grid, amount: float, uncertainty: Grid):
f_uncertainty: math.Tensor = math.sqrt(math.sum(uncertainty.values ** 2, dim='x,y')) # all frequencies have the same uncertainty, 1/N in iFFT
k_squared: math.Tensor = math.sum(math.fftfreq(grid.shape, grid.dx) ** 2, 'vector')
fft_laplace: math.Tensor = -(2 * np.pi) ** 2 * k_squared
# --- Compute sharpening kernel with damping ---
log_kernel = fft_laplace * -amount
log_kernel_clamped = math.minimum(log_kernel, math.to_float(math.floor(math.log(math.wrap(np.finfo(np.float32).max))))) # avoid overflow
raw_kernel = math.exp(log_kernel_clamped) # inverse diffusion FFT kernel, all values >= 1
inv_kernel = math.exp(-log_kernel)
amp = math.fft(grid.values)
kernel, sig_prob = apply_damping(raw_kernel, inv_kernel, amp, f_uncertainty, log_kernel)
# --- Apply and compute uncertainty ---
data = math.real(math.ifft(amp * math.to_complex(kernel)))
uncertainty = math.sqrt(math.sum(((f_uncertainty * kernel) ** 2))) / grid.shape.get_size('x') # 1/N normalization in iFFT
uncertainty = grid * 0 + uncertainty
return grid.with_values(data), uncertainty, abs(amp), raw_kernel, kernel, sig_prob
20.6 神经网络和损失函数
对于神经网络,我们使用简单的U-net架构来处理SIP,以及常规的DP+Adam版本(与前面的部分一致,我们将其表示为“GD”)。我们使用批量大小为128和恒定学习率进行训练,对于物理部分使用64位精度,对于网络部分使用32位精度。网络更新使用TensorFlow或PyTorch的自动微分计算。
math.set_global_precision(64)
BATCH = batch(batch=128)
STEPS = 50
math.seed(0)
net = u_net(1, 1)
optimizer = adam(net, 0.001)
现在我们将为phiflow定义损失函数。网络权重的梯度总是计算为。
对于SIP,我们反演物理过程,然后将代理损失定义为(prediction - correction),其中correction被视为常数。通过x = field.stop_gradient(prediction)来实现这一点。这个L2损失触发了对神经网络权重的反向传播。对于SIP,y_l2仅用于比较,对训练不是关键。
对于sip=False的Adam / GD版本,简单地计算预测的扩散场与目标之间的L2差异,并通过梯度传播操作进行反向传播。
我们还实时计算损失函数中的参考。
# @math.jit_compile
def loss_function(net, x_gt: CenteredGrid, sip: bool):
y_target = diffuse.fourier(x_gt, 8., 1)
with math.precision(32):
prediction = field.native_call(net, field.to_float(y_target)).vector[0]
prediction += field.mean(x_gt) - field.mean(prediction)
x = field.stop_gradient(prediction)
if sip:
y = diffuse.fourier(x, 8., 1)
dx, _, amp, raw_kernel, kernel, sig_prob = inv_diffuse(y_target - y, 8., uncertainty=abs(y_target - y) * 1e-6)
correction = x + dx
y_l2 = field.l2_loss(y - y_target) # not important, just for tracking
loss = field.l2_loss(prediction - correction) # proxy L2 loss for network
else:
y = diffuse.fourier(prediction, 8., 1)
loss = y_l2 = field.l2_loss(y - y_target) # for Adam we backprop through the loss and y
return loss, x, y, field.l2_loss(x_gt - x), y_l2
20.7 训练
在训练循环中,我们通过generate_heat_example()实时生成数据,并使用phiflow的update_weights()函数调用所选择后端的正确函数。请注意,为了清晰起见,下面只打印了前5步的损失值,完整的历史记录保存在loss_列表中。下面的单元格运行SIP版本的训练:
loss_sip_x=[]; loss_sip_y=[]
for training_step in range(STEPS):
data = generate_heat_example(spatial(x=64, y=64), BATCH)
loss_value, x_sip, y_sip, x_l2, y_l2 = update_weights(net, optimizer, loss_function, net, data, sip=True)
loss_sip_x.append(float(x_l2.mean))
loss_sip_y.append(float(y_l2.mean))
if(training_step<5): print("SIP L2 loss x ; y: "+format(float(x_l2.mean))+" ; "+format(float(y_l2.mean)) )
SIP L2 loss x ; y: 187.2586057892786 ; 59.48433060883144
SIP L2 loss x ; y: 70.21347147390776 ; 13.783476203544797
SIP L2 loss x ; y: 51.91472605336263 ; 5.72813432496525
SIP L2 loss x ; y: 39.46109317565444 ; 4.4424629873554045
SIP L2 loss x ; y: 34.611490797378366 ; 3.359133206049436
现在我们可以使用Adam算法对DP版本进行训练,通过sip=False来禁用SIP更新。
math.seed(0)
net_gd = u_net(1, 1)
optimizer_gd = adam(net_gd, 0.001)
loss_gd_x=[]; loss_gd_y=[]
for training_step in range(STEPS):
data = generate_heat_example(spatial(x=64, y=64), BATCH)
loss_value, x_gd, y_gd, x_l2, y_l2 = update_weights(net_gd, optimizer_gd, loss_function, net_gd, data, sip=False)
loss_gd_x.append(float(x_l2.mean))
loss_gd_y.append(float(y_l2.mean))
if(training_step<5): print("GD L2 loss x ; y: "+format(float(x_l2.mean))+" ; "+format(float(y_l2.mean)) )
GD L2 loss x ; y: 187.2586057892786 ; 59.48433060883144
GD L2 loss x ; y: 104.37856249315794 ; 20.323700695817763
GD L2 loss x ; y: 72.5135221242247 ; 7.211550418534284
GD L2 loss x ; y: 59.74792697261851 ; 5.3912096056107135
GD L2 loss x ; y: 50.49939087445511 ; 3.6758429757536093
20.8 评估
现在我们可以直接比较这两个变体的表现。需要注意的是,由于随机数据的即时生成,所有样本都是之前未见过的,因此我们将直接使用训练曲线来得出这两种方法的性能结论。
下图显示了关于重建输入的误差在训练过程中的变化,这是我们训练的主要目标。
import pylab as plt
fig = plt.figure().gca()
pltx = range(len(loss_gd_x))
fig.plot(pltx, loss_gd_x , lw=2, color='blue', label="GD")
fig.plot(pltx, loss_sip_x , lw=2, color='red', label="SIP")
plt.xlabel('iterations'); plt.ylabel('x loss'); plt.legend(); plt.yscale("log")
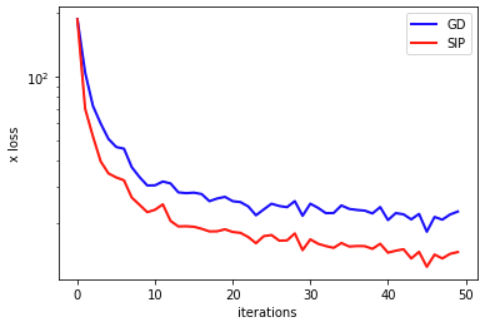
在的损失的对数尺度上,SIP版本的显著优势得到了很好的突出,表明了神经网络训练的收敛性显著改善。这纯粹是由于通过代理损失函数提供给物理学的更好信号所致。如loss_function()所示,两个变体都使用基于反向传播的更新方法来改变神经网络的权重。改进纯粹来自通过逆模拟器计算的空间中的高阶步骤。
出于好奇,我们还可以比较这两个版本在输出空间的差异方面的比较。
fig = plt.figure().gca()
pltx = range(len(loss_gd_y))
import scipy # for filtering
fig.plot(pltx, scipy.ndimage.filters.gaussian_filter1d(loss_gd_y,sigma=2) , lw=2, color='blue', label="GD")
fig.plot(pltx, scipy.ndimage.filters.gaussian_filter1d(loss_sip_y ,sigma=2), lw=2, color='red', label="SIP")
plt.xlabel('iterations'); plt.ylabel('y loss'); plt.legend(); plt.yscale("log")

SIPs也有改进,但与空间相比,改进并不明显。幸运的是,重建是主要目标,因此对于当前的逆问题而言,它具有更高的重要性。
通过直接比较,误差方面的差异也非常明显。下面的单元格将GD和Adam的重建结果与SIP版本以及真实值进行对比。差异是显而易见的:SIP重建明显更锐利,且比GD版本包含更少的光晕。这是由于GD应用扩散到反向传播的梯度上,而不是与之相抵消的不良行为所导致的。
plt = vis.plot(x_gd.values.batch[0], x_sip.values.batch[0], data.values.batch[0], size=(15,4) )
plt.get_axes()[0].set_title("Adam"); plt.get_axes()[1].set_title("SIP"); plt.get_axes()[2].set_title("Reference");

20.9 下一步
- 针对此示例,值得尝试各种训练参数:延长训练时间,使用不同的学习速率和网络规模(甚至不同的体系结构)。
前几章的尺度不变物理更新(SIP)阐明了“反演”更新步骤方向(除了利用更高阶项)的重要性。现在我们将转向另一种实现反演的方法,即所谓的“半反演梯度”(HIG){cite}schnell2022hig。它们具有自己的优点和缺点,因此为基于物理的深度学习任务计算改进的更新步骤提供了有趣的替代方案。
与SIP不同,它们不需要解析反演求解器。HIG同时反演神经网络部分和物理模型。作为缺点,它们需要对大型雅可比矩阵进行奇异值分解。
更具体地说,HIGs(Hierarchical Inverse Graphics)不需要解析逆求解器(与SIPs相比),并且它们同时对神经网络部分和物理模型进行反演。作为一个缺点,HIGs需要对一个大的雅可比矩阵进行奇异值分解,并且基于一阶信息(类似于常规梯度)。然而,与常规梯度不同的是,它们使用完整的雅可比矩阵。因此,正如我们将在下面看到的,它们通常明显优于常规的梯度下降法(GD)和Adam算法。
21.1 推导
正如在{eq}quasi-newton-update中推导逆模拟器更新时所提到的,对于常规的牛顿步骤,更新使用了逆Hessian矩阵。如果我们将其更新重写为损失的情况下,我们得到了Gauss-Newton(GN)方法:
对于满秩雅可比矩阵 ,其转置雅可比矩阵抵消,方程简化为:
这看起来更简单,但仍然需要我们求解雅可比矩阵的逆。这个雅可比矩阵通常是非方阵,并且具有导致求逆过程中出现问题的小奇异值。简单地应用高斯-牛顿等方法可能会迅速失效。然而,由于我们处理的是在训练环节中有物理求解器的情况,这些小奇异值通常与物理有关。因此,我们不希望仅仅丢弃学习信号中的这部分内容,而是尽可能保留其中的许多部分。
这激发了HIG更新方法,它采用了部分和截断的逆形式。
在这一步骤中,通过奇异值分解计算的平方根,并表示为半逆。即对于矩阵,我们通过奇异值分解计算其半逆,如,其中包含奇异值。 在这一步中,我们还可以处理小奇异值形式的数值噪声。将中小于阈值的所有元素设为零。
截断与夹紧:一开始,将奇异值夹紧到一个小值,而不是通过将其设为零来丢弃它们,可能看起来很有吸引力。然而,与这些小奇异值相对应的奇异向量恰恰是潜在不可靠的向量。一个小的τ在求逆过程中会产生很大的贡献,因此当进行夹紧时,这些奇异向量会引发问题。因此,通过将它们的奇异值设为零来丢弃它们的内容是一个更好的主意。
使用的部分逆代替的完全逆有助于防止小特征值在更新步骤中产生过大的贡献。这是受Adam方法的启发,后者通过而非对搜索方向进行归一化,其中是雅可比矩阵的对角线。对于Adam,由于对角线的粗略近似,这种折中是必要的。对于HIGs,我们使用完整的雅可比矩阵,因此可以进行适当的逆运算。然而,正如原始论文{cite}schnell2022hig所述,半逆运算规范化了逆运算,并为学习提供了实质性的改进,同时降低了梯度爆炸的风险。
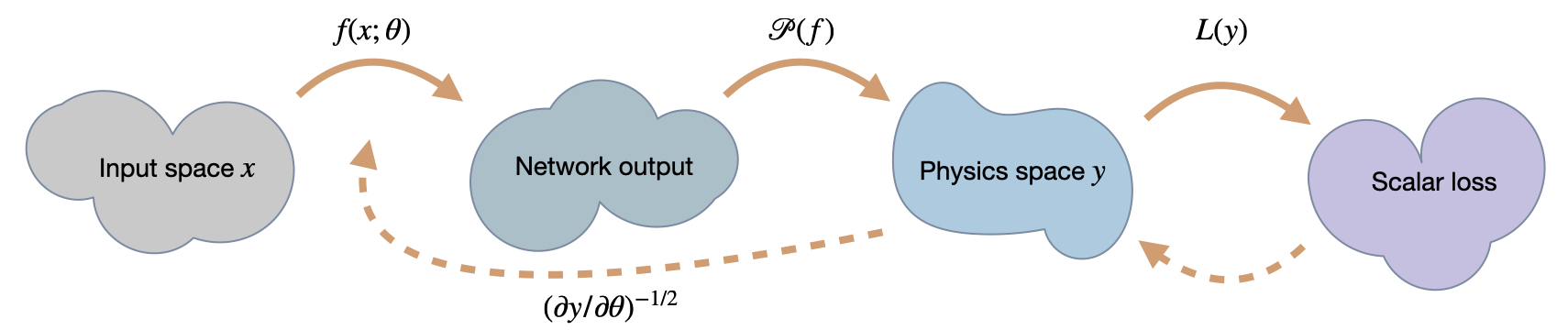
21.2 构造雅可比矩阵
上述公式隐藏了HIG的一个重要方面:我们计算的搜索方向不仅考虑了神经网络和物理的缩放,还可以结合mini-batch中所有样本的信息。这样做的优点是可以找到最优的方向(在意义下)来最小化损失,而不是像GD或Adam一样对方向进行平均。
为了实现这一点,将的Jacobian矩阵从mini-batch中每个样本的个别Jacobian拼接而成。设分别表示mini-batch中第个样本的输入和输出,则最终的Jacobian通过所有的构建而成。
使用的符号也清楚地表明了雅可比矩阵的所有部分是根据相应的输入状态进行评估的。与常规优化不同,其中较大的批次通常由于平均效果而不会有太大回报,而HIG对批次大小有更强的依赖性。它们通常从更大的小批量大小中获益。
总结一下,计算HIG更新需要评估批次的各个雅可比矩阵,对组合雅可比矩阵进行奇异值分解,截断和半逆奇异值,并通过重新组装半逆雅可比矩阵来计算更新方向。

21.3 通过 Toy 示例说明性质
这是一个展示前文提到的性质的好时机,我们将通过一个真实的例子来说明。作为学习目标,我们将考虑一个简单的二维情境,其中包含函数。
以及一个缩放的损失函数
这里的和分别表示的第一和第二个分量(与上面的小批量条目的下标相对应)。注意,通过进行的缩放只应用于损失的第二个分量。这模拟了在物理模拟设置中常遇到的两个分量的不均匀缩放,其量可以通过选择。
我们将使用一个由7个神经元组成的单隐藏层的小型神经网络,其激活函数为tanh(),目标是学习。
21.4 良好条件
让我们首先看一下在的情况下,条件良好的情况。在下面的图像中,我们将比较Adam作为最流行的梯度下降代表、高斯-牛顿(GN)作为“经典”方法以及HIGs。这些方法将根据三个方面进行评估:首先,观察损失的演变是很有趣的。此外,我们还将考虑神经网络状态的神经元激活分布(稍后详细介绍)。最后,观察优化如何影响神经网络产生的目标状态(在空间中)。请注意,下面的空间图表仅显示一个单一但相当代表性的对。其他两个图表显示了更大一组验证输入的数量。
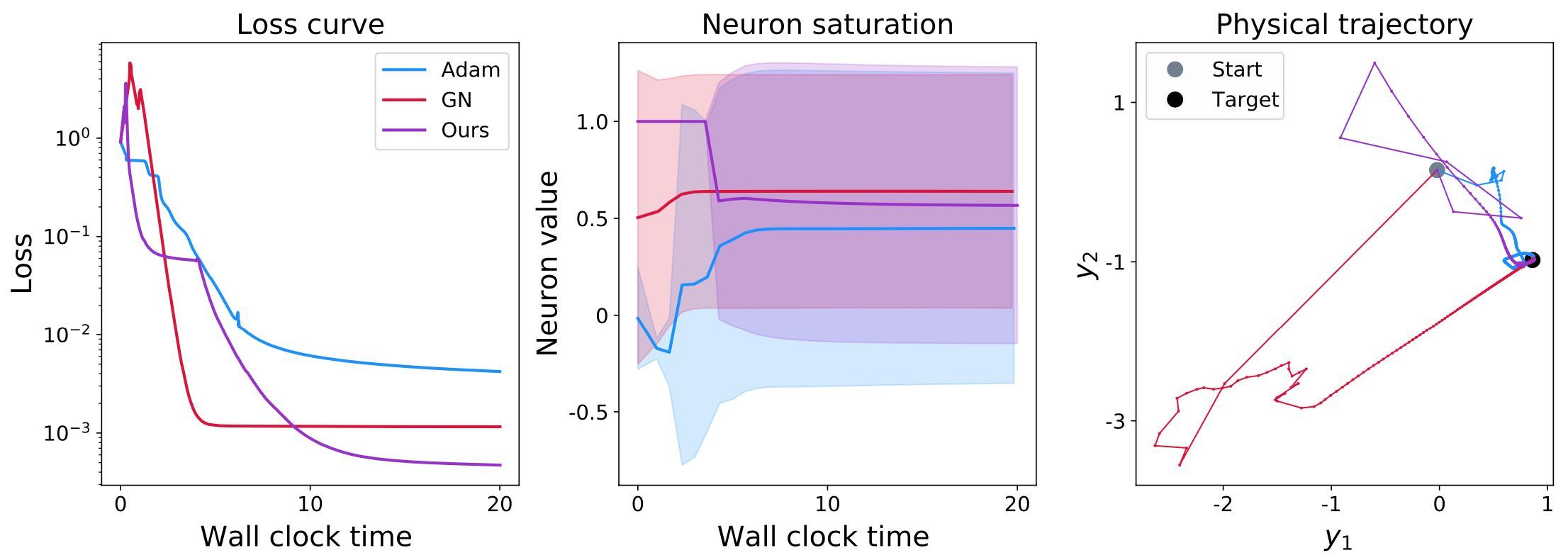
如图所示,在条件良好的情况下,所有三种方法在各个方面表现都还可以:损失降低到约和左右。
此外,神经元的激活情况(以均值和标准差表示)显示出一系列广泛的数值范围(由表示标准差的实心阴影区域表示)。这意味着所有三个网络的神经元产生了广泛的数值范围。虽然在这里很难解释具体的数值,但不同的输入产生不同的数值是一个好迹象。如果不是这种情况,即不同的输入产生恒定的数值(尽管目标显然不同),那将是一个非常不好的迹象。这通常是由于完全饱和的神经元状态被过大的更新步骤“破坏”造成的。但对于这个条件良好的示例,这种饱和现象并没有出现。
最后,右侧的第三个图显示了一个输入-输出对的演变过程。初始网络状态的起点显示为浅灰色,而地面真实目标显示为一个黑点。最重要的是,所有三种方法最终都能达到黑点。对于这个简单的示例,看到这一点并不令人过分惊讶。然而,有趣的是,GN和HIG在学习过程的初始阶段(离开灰点的前几个部分)都存在较大的跳跃。这是由于初始状态相当糟糕以及反演引起的,导致了神经网络状态及其输出的显著变化。相比之下,Adam的动量项减少了这种跳跃性:浅蓝色线条的初始跳跃比其他两种方法小。
总体而言,所有三种方法的行为基本符合我们的预期:虽然损失肯定可以进一步降低,而且中的一些步骤似乎暂时朝着错误的方向发展,但这三种方法在这种情况下都表现得相当好。毫不奇怪,当使用小的导致条件更差的雅可比矩阵时,情况将会发生变化。
21.5 病态条件
现在我们考虑一个条件较差的情况,其中。在实际的PDE求解器中,情况可能会更糟,但有趣的是,这个的因子足以说明实践中出现的问题。以下是同一组3张图的条件较差的情况:
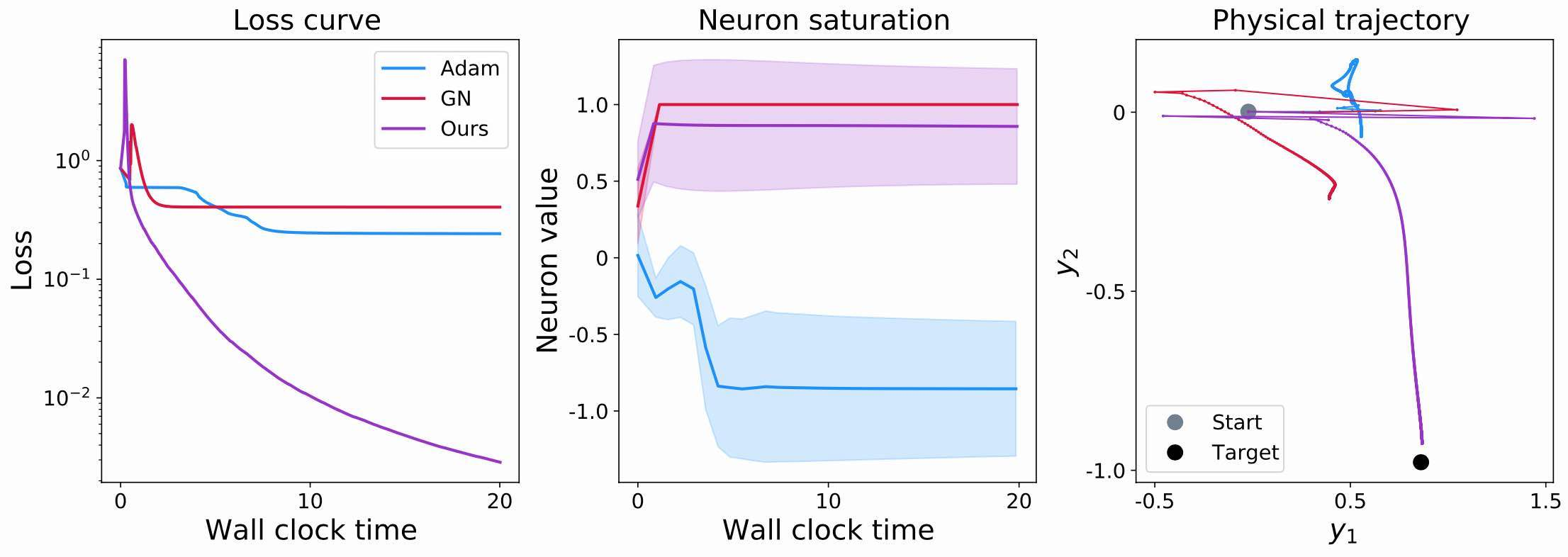
现在的损失曲线显示出不同的行为:Adam和GN都无法将损失降低到约0.2的水平以下(与之前的0.01及更好相比)。Adam在分量的不良缩放方面存在显著问题,无法正确收敛。对于GN来说,雅可比矩阵的完全反转会导致梯度爆炸,破坏反转的积极效果。更糟糕的是,它们会导致神经网络有效地卡住。
这在中间的图表中变得更加清晰,它显示了激活统计数据。GN的红色曲线很快饱和在1处,没有显示任何方差。因此,所有的神经元都饱和了,不再产生有意义的信号。这不仅意味着目标函数没有被很好地逼近,而且意味着未来的梯度将有效地为零,并且这些神经元将在所有未来的学习迭代中丢失。因此,这是一种高度不可取的情况,我们希望在实践中避免。值得指出的是,这并不总是发生在GN上。然而,它经常发生,例如当批次中的个别样本导致雅可比矩阵中的向量线性相关(或非常接近)时,从而使GN成为次优选择。
右侧图{numref}hig-toy-example-bad的第三个图表显示了输出的结果。正如损失值所示,Adam和GN都没有达到目标(黑点)。有趣的是,它们在方向上遇到了更多的问题,我们用它来引起不良条件:它们都在图表的x轴()上取得了一些进展,但在朝向目标值方向上没有太多的移动。这说明了上面的讨论:GN由于饱和的神经元而卡住,而Adam则难以撤销的缩放。
21.6 半逆梯度小结
请注意,到目前为止,我们已经改进了前几章中的可微物理(DP)训练的所有示例。也就是说,我们专注于神经网络和PDE求解算子的组合。后者需要在常规GD训练和HIG训练中可微分。
相反,对于使用SIPs(来自{doc}physgrad-nn)进行训练,我们甚至需要提供完整的反演求解器。正如在那里所示,这具有优势,但将SIP与DP和HIG区分开来。因此,HIG与例如{doc}diffphys-code-sol和{doc}diffphys-code-control的相似之处更多,而不是示例{doc}physgrad-code。
现在是时候给出一个具体的代码示例,展示如何使用HIG训练物理神经网络:我们将看一个经典案例,即一组耦合振子系统。
在本笔记本中,我们将通过一个实际例子来比较半反梯度(HIGs)与其他用于训练具有物理损失函数的神经网络的方法。具体而言,我们将比较以下几种方法:
- Adam:作为标准的基于梯度下降(GD)的网络优化器,
- 尺度不变物理学:先前描述的完全反演物理学的算法,
- 半逆梯度:在局部和联合反演物理学和网络。
22.1 反问题设置
学习任务是找到控制函数来控制耦合振荡器系统的动力学。这是物理学中的一个经典问题,也是一个评估HIGs的好案例,因为它的规模较小。我们使用两个质点,因此对于两个质点的位置和速度,我们只有四个自由度(相对于例如仅具有32个单元格沿x和y的“小”流体模拟,我们将获得个未知数)。
尽管如此,振荡器是一个高度非平凡的案例:我们的目标是应用控制,使得在选择的时间间隔后再次达到初始状态。我们将使用24步四阶Runge-Kutta方案,因此NN必须学习如何在所有时间步骤中最好地“推动”两个质点,使它们在正确的时间以正确的速度到达所需的位置。
一个由个耦合振子组成的系统可以用以下哈密顿量描述:
它为下面的 RK 4 时间积分提供了基础。
22.2 问题描述
更具体地说,我们考虑一组不同的物理输入()。通过使用相应的控制函数(),我们可以影响我们的物理系统的时间演化并获得一个输出状态():
如果我们想将给定的初始状态()演化为给定的目标状态(),我们就会得到一个控制函数()的反问题。期望目标状态()与接收到的目标状态()之间的质量由损失函数()来衡量。
如果我们使用一个神经网络(参数化为)来学习一组输入/输出对()上的控制函数,我们将上述物理优化任务转化为一个学习问题。
在设置物理求解器之前,我们导入必要的库(本例使用TensorFlow),并定义主要的全局变量MODE,它在_Adam_('GD')、尺度不变物理('SIP')和_半反梯度_('HIG')之间切换。
import numpy as np
import tensorflow as tf
import time, os
# main switch for the three methods:
MODE = 'HIG' # HIG | SIP | GD
22.3 耦合线性振子模拟
对于物理模拟,我们将解决一个耦合线性振子系统带有控制项的微分方程。时间积分使用四阶龙格-库塔方案。
下面,我们首先定义一些全局常量:Nx:振子的数量,Nt:时间演化步数,以及DT:一个时间步长的长度。然后我们定义一个帮助函数来设置一个拉普拉斯模板,名为coupled_oscillators_batch()的函数计算整个小批量值的模拟,最后是solver()函数,它使用给定的控制信号运行所需的时间步数。
Nx = 2
Nt = 24
DT = 0.5
def build_laplace(n,boundary='0'):
if n==1:
return np.zeros((1,1),dtype=np.float32)
d1 = -2 * np.ones((n,),dtype=np.float32)
d2 = 1 * np.ones((n-1,),dtype=np.float32)
lap = np.zeros((n,n),dtype=np.float32)
lap[range(n),range(n)]=d1
lap[range(1,n),range(n-1)]=d2
lap[range(n-1),range(1,n)]=d2
if boundary=='0':
lap[0,0]=lap[n-1,n-1]=-1
return lap
@tf.function
def coupled_oscillators_batch( x, control):
'''
ODE of type: x' = f(x)
:param x_in: position and velocities, shape: (batch, 2 * number of osc) order second index: x_i , v_i
:param control: control function, shape: (batch,)
:return:
'''
#print('coupled_oscillators_batch')
n_osc = x.shape[1]//2
# natural time evo
a1 = np.array([[0,1],[-1,0]],dtype=np.float32)
a2 = np.eye(n_osc,dtype=np.float32)
A = np.kron(a1,a2)
x_dot1 = tf.tensordot(x,A,axes = (1,1))
# interaction term
interaction_strength = 0.2
b1 = np.array([[0,0],[1,0]],dtype=np.float32)
b2 = build_laplace(n_osc)
B = interaction_strength * np.kron(b1,b2)
x_dot2 = tf.tensordot(x,B, axes=(1, 1))
# control term
control_vector = np.zeros((n_osc,),dtype=np.float32)
control_vector[-1] = 1.0
c1 = np.array([0,1],dtype=np.float32)
c2 = control_vector
C = np.kron(c1,c2)
x_dot3 = tf.tensordot(control,C, axes=0)
#all terms
x_dot = x_dot1 + x_dot2 +x_dot3
return x_dot
@tf.function
def runge_kutta_4_batch(x_0, dt, control, ODE_f_batch):
f_0_0 = ODE_f_batch(x_0, control)
x_14 = x_0 + 0.5 * dt * f_0_0
f_12_14 = ODE_f_batch(x_14, control)
x_12 = x_0 + 0.5 * dt * f_12_14
f_12_12 = ODE_f_batch(x_12, control)
x_34 = x_0 + dt * f_12_12
terms = f_0_0 + 2 * f_12_14 + 2 * f_12_12 + ODE_f_batch(x_34, control)
x1 = x_0 + dt * terms / 6
return x1
@tf.function
def solver(x0, control):
x = x0
for i in range(Nt):
x = runge_kutta_4_batch(x, DT, control[:,i], coupled_oscillators_batch)
return x
22.4 训练设置
神经网络本身非常简单:它由四个密集层组成(中间的每个层有20个神经元),并使用tanh激活函数。
act = tf.keras.activations.tanh
model = tf.keras.models.Sequential([
tf.keras.layers.InputLayer(input_shape=(2*Nx)),
tf.keras.layers.Dense(20, activation=act),
tf.keras.layers.Dense(20, activation=act),
tf.keras.layers.Dense(20, activation=act),
tf.keras.layers.Dense(Nt, activation='linear')
])
作为损失函数, 我们将使用 损失:
@tf.function
def loss_function(a,b):
diff = a-b
loss_batch = tf.reduce_sum(diff**2,axis=1)
loss = tf.reduce_sum(loss_batch)
return loss
作为训练的数据集,我们简单地创建了4k个随机位置值,这些位置值是振荡器在模拟开始时的初始状态(X_TRAIN),并且在模拟结束时应该返回到这些初始状态(Y_TRAIN)。由于它们应该返回到初始状态,我们有X_TRAIN=Y_TRAIN。
N = 2**12
X_TRAIN = np.random.rand(N, 2 * Nx).astype(np.float32)
Y_TRAIN = X_TRAIN # the target states are identical
22.5 训练
神经网络训练的优化过程需要设置一些全局参数。下一个单元格初始化了适合三种方法的一些合适值。这些值是根据经验确定的,对于每种方法都能够发挥最佳效果。如果我们尝试为所有方法使用相同的设置,这将不可避免地使其中一些方法的比较不公平。
-
Adam:这是最广泛使用的神经网络优化器,我们在这里使用它作为GD家族的代表。请注意,截断参数对Adam没有意义。
-
SIP:指定的优化器是用于网络优化的。物理反演是通过高斯-牛顿完成的,并且对应于精确反演,因为物理优化景观是二次的。对于高斯-牛顿中的雅可比矩阵反演,我们可以指定截断参数。
-
HIG:要获得HIG算法,必须将优化器设置为SGD。对于雅可比矩阵的半反演,我们可以指定截断参数。最佳批量大小通常比其他两种方法要低,学习率为1通常非常有效。
最大训练时间以秒为单位通过下面的 MAX_TIME 设置。
if MODE=='HIG': # HIG training
OPTIMIZER = tf.keras.optimizers.SGD
BATCH_SIZE = 32 # larger batches make HIGs unnecessariy slow...
LR = 1.0
TRUNC = 10**-10
elif MODE=='SIP': # SIP training
OPTIMIZER = tf.keras.optimizers.Adam
BATCH_SIZE = 256
LR = 0.001 # for the internal step with Adam
TRUNC = 0 # not used
else: # Adam Training (as GD representative)
MODE = 'GD'
OPTIMIZER = tf.keras.optimizers.Adam
BATCH_SIZE = 256
LR = 0.001
TRUNC = 0 # not used
# global parameters for all three methods
MAX_TIME = 100 # [s]
print("Running variant: "+MODE)
输出结果:
Running variant: HIG
下一个函数HIG_pinv()是一个关键函数:它用于构建给定HIGs矩阵的半逆。它计算SVD,取奇异值的平方根,然后重新组装矩阵。
from tensorflow.python.framework import ops
from tensorflow.python.framework import tensor_shape
from tensorflow.python.ops import array_ops
from tensorflow.python.ops import math_ops
from tensorflow.python.util import dispatch
from tensorflow.python.util.tf_export import tf_export
from tensorflow.python.ops.linalg.linalg_impl import _maybe_validate_matrix,svd
# partial inversion of the Jacobian via SVD:
# this function is adopted from tensorflow's SVD function, and published here under its license: Apache-2.0 License , https://github.com/tensorflow/tensorflow/blob/master/LICENSE
@tf_export('linalg.HIG_pinv')
@dispatch.add_dispatch_support
def HIG_pinv(a, rcond=None,beta=0.5, validate_args=False, name=None):
with ops.name_scope(name or 'pinv'):
a = ops.convert_to_tensor(a, name='a')
assertions = _maybe_validate_matrix(a, validate_args)
if assertions:
with ops.control_dependencies(assertions):
a = array_ops.identity(a)
dtype = a.dtype.as_numpy_dtype
if rcond is None:
def get_dim_size(dim):
dim_val = tensor_shape.dimension_value(a.shape[dim])
if dim_val is not None:
return dim_val
return array_ops.shape(a)[dim]
num_rows = get_dim_size(-2)
num_cols = get_dim_size(-1)
if isinstance(num_rows, int) and isinstance(num_cols, int):
max_rows_cols = float(max(num_rows, num_cols))
else:
max_rows_cols = math_ops.cast(
math_ops.maximum(num_rows, num_cols), dtype)
rcond = 10. * max_rows_cols * np.finfo(dtype).eps
rcond = ops.convert_to_tensor(rcond, dtype=dtype, name='rcond')
[ singular_values, left_singular_vectors, right_singular_vectors, ] = svd(
a, full_matrices=False, compute_uv=True)
cutoff = rcond * math_ops.reduce_max(singular_values, axis=-1)
singular_values = array_ops.where_v2(
singular_values > array_ops.expand_dims_v2(cutoff, -1), singular_values**beta,
np.array(np.inf, dtype))
a_pinv = math_ops.matmul(
right_singular_vectors / array_ops.expand_dims_v2(singular_values, -2),
left_singular_vectors,
adjoint_b=True)
if a.shape is not None and a.shape.rank is not None:
a_pinv.set_shape(a.shape[:-2].concatenate([a.shape[-1], a.shape[-2]]))
return a_pinv
现在我们已经准备好运行训练了。下一个单元格定义了一个Python类来组织神经网络优化。它接收物理求解器、网络模型、损失函数和数据集,并在给定的时间限制MAX_TIME内运行尽可能多的周期。
根据选择的优化方法,小批量更新有所不同:
- Adam:计算损失梯度,然后应用Adam更新。
- PG:计算损失梯度和物理雅可比矩阵,逐个数据点地求逆,通过代理损失和Adam计算网络更新。
- HIG:计算损失梯度和网络-物理雅可比矩阵,然后联合计算半求逆,并使用得到的步长更新网络参数。
优化器类的mini_batch_update()方法实现了这三种变体。
class Optimization():
def __init__(self,model,solver,loss_function,x_train,y_train):
self.model = model
self.solver = solver
self.loss_function = loss_function
self.x_train = x_train
self.y_train = y_train
self.y_dim = y_train.shape[1]
self.weight_shapes = [weight_tensor.shape for weight_tensor in self.model.trainable_weights]
def set_params(self,batch_size,learning_rate,optimizer,max_time,mode,trunc):
self.number_of_batches = N // batch_size
self.max_time = max_time
self.batch_size = batch_size
self.learning_rate = learning_rate
self.optimizer = optimizer(learning_rate)
self.mode = mode
self.trunc = trunc
def computation(self,x_batch, y_batch):
control_batch = self.model(y_batch)
y_prediction_batch = self.solver(x_batch,control_batch)
loss = self.loss_function(y_batch,y_prediction_batch)
return loss
@tf.function
def gd_get_derivatives(self,x_batch, y_batch):
with tf.GradientTape(persistent=True) as tape:
tape.watch(self.model.trainable_variables)
loss = self.computation(x_batch,y_batch)
loss_per_dp = loss / self.batch_size
grad = tape.gradient(loss_per_dp, self.model.trainable_variables)
return grad
@tf.function
def pg_get_physics_derivatives(self,x_batch, y_batch): # physics gradient for SIP
with tf.GradientTape(persistent=True) as tape:
control_batch = self.model(y_batch)
tape.watch(control_batch)
y_prediction_batch = self.solver(x_batch,control_batch)
loss = self.loss_function(y_batch,y_prediction_batch)
loss_per_dp = loss / self.batch_size
jacy = tape.batch_jacobian(y_prediction_batch,control_batch)
grad = tape.gradient(loss_per_dp, y_prediction_batch)
return jacy,grad,control_batch
@tf.function
def pg_get_network_derivatives(self,x_batch, y_batch,new_control_batch): #physical grads
with tf.GradientTape(persistent=True) as tape:
tape.watch(self.model.trainable_variables)
control_batch = self.model(y_batch)
loss = self.loss_function(new_control_batch,control_batch)
#y_prediction_batch = self.solver(x_batch,control_batch)
#loss = self.loss_function(y_batch,y_prediction_batch)
loss_per_dp = loss / self.batch_size
network_grad = tape.gradient(loss_per_dp, self.model.trainable_variables)
return network_grad
@tf.function
def hig_get_derivatives(self,x_batch,y_batch):
with tf.GradientTape(persistent=True) as tape:
tape.watch(self.model.trainable_variables)
control_batch = self.model(y_batch)
y_prediction_batch = self.solver(x_batch,control_batch)
loss = self.loss_function(y_batch,y_prediction_batch)
loss_per_dp = loss / self.batch_size
jacy = tape.jacobian(y_prediction_batch, self.model.trainable_variables, experimental_use_pfor=True)
loss_grad = tape.gradient(loss_per_dp, y_prediction_batch)
return jacy, loss_grad
def mini_batch_update(self,x_batch, y_batch):
if self.mode=="GD":
grad = self.gd_get_derivatives(x_batch, y_batch)
self.optimizer.apply_gradients(zip(grad, self.model.trainable_weights))
elif self.mode=="SIP":
jacy,grad,control_batch = self.pg_get_physics_derivatives(x_batch, y_batch)
grad_e = tf.expand_dims(grad,-1)
pinv = tf.linalg.pinv(jacy,rcond=10**-5)
delta_control_label_batch = (pinv@grad_e)[:,:,0]
new_control_batch = control_batch - delta_control_label_batch
network_grad = self.pg_get_network_derivatives(x_batch, y_batch,new_control_batch)
self.optimizer.apply_gradients(zip(network_grad, self.model.trainable_weights))
elif self.mode =='HIG':
jacy, grad = self.hig_get_derivatives(x_batch, y_batch)
flat_jacy_list = [tf.reshape(jac, (self.batch_size * self.y_dim, -1)) for jac in jacy]
flat_jacy = tf.concat(flat_jacy_list, axis=1)
flat_grad = tf.reshape(grad, (-1,))
inv = HIG_pinv(flat_jacy, rcond=self.trunc)
processed_derivatives = tf.tensordot(inv, flat_grad, axes=(1, 0))
#processed_derivatives = self.linear_solve(flat_jacy, flat_grad)
update_list = []
l1 = 0
for k, shape in enumerate(self.weight_shapes):
l2 = l1 + np.prod(shape)
upd = processed_derivatives[l1:l2]
upd = np.reshape(upd, shape)
update_list.append(upd)
l1 = l2
self.optimizer.apply_gradients(zip(update_list, self.model.trainable_weights))
def epoch_update(self):
for batch_index in range(self.number_of_batches):
position = batch_index * self.batch_size
x_batch = self.x_train[position:position + self.batch_size]
y_batch = self.y_train[position:position + self.batch_size]
self.mini_batch_update(x_batch, y_batch)
def eval(self,epoch,wc_time,ep_dur):
train_loss = self.computation(self.x_train,self.y_train)
train_loss_per_dp = train_loss / N
if epoch<5 or epoch%20==0: print('Epoch: ', epoch,', wall clock time: ',wc_time,', loss: ', float(train_loss_per_dp) )
#print('TrainLoss:', train_loss_per_dp)
#print('Epoch: ', epoch,' WallClockTime: ',wc_time,' EpochDuration: ',ep_dur )
return train_loss_per_dp
def start_training(self):
init_loss = self.eval(0,0,0)
init_time = time.time()
time_list = [init_time]
loss_list = [init_loss]
epoch=0
wc_time = 0
while wc_time<self.max_time:
duration = time.time()
self.epoch_update()
duration = time.time()-duration
epoch += 1
wc_time += duration
loss = self.eval(epoch,wc_time,duration)
time_list.append(duration)
loss_list.append(loss)
time_list = np.array(time_list)
loss_list = np.array(loss_list)
time_list[0] = 0
return time_list, loss_list
剩下的就是使用选择的全局参数开始训练,并将结果收集在time_list和loss_list中。
opt = Optimization(model, solver, loss_function, X_TRAIN, Y_TRAIN)
opt.set_params(BATCH_SIZE, LR, OPTIMIZER, MAX_TIME, MODE, TRUNC)
time_list, loss_list = opt.start_training()
Epoch: 0 , wall clock time: 0 , loss: 1.4401766061782837
Epoch: 1 , wall clock time: 28.06755018234253 , loss: 5.44398972124327e-05
Epoch: 2 , wall clock time: 31.38792371749878 , loss: 1.064436037268024e-05
Epoch: 3 , wall clock time: 34.690271854400635 , loss: 3.163525434501935e-06
Epoch: 4 , wall clock time: 37.9914448261261 , loss: 1.1857609933940694e-06
22.6 评估
现在我们可以评估培训过程随时间的收敛情况。以下图表显示了损失随时间(以秒为单位)的演变。
import matplotlib.pyplot as plt
plt.plot(np.cumsum(time_list),loss_list)
plt.yscale('log')
plt.xlabel('Wall clock time [s]'); plt.ylabel('Loss')
plt.title('Linear chain - '+MODE+' with '+str(OPTIMIZER.__name__))
plt.show()
对于这三种方法,你会看到一个很大的线性步骤,就在开始时。由于我们正在公平地测量整个运行时间,因此这个第一步包括了所有TensorFlow初始化步骤,对于HIG和SIP而言,这些步骤显著更为复杂。Adam在初始化方面要快得多,并且每个训练迭代也同样更快。
这三种方法本身都能降低损失。更有趣的是看它们如何比较。为此,下一个单元格会存储训练演变,并且需要使用这三种方法中的每一种运行一次来生成最终的比较图。
path = '/home/'
namet = 'time'
namel = 'loss'
np.savetxt(path+MODE+namet+'.txt',time_list)
np.savetxt(path+MODE+namel+'.txt',loss_list)
在使用每种方法进行运行后,我们可以将它们并列显示:
from os.path import exists
# if previous runs are available, compare all 3
if exists(path+'HIG'+namet+'.txt') and exists(path+'HIG'+namel+'.txt') and exists(path+'SIP'+namet+'.txt') and exists(path+'SIP'+namel+'.txt') and exists(path+'GD'+namet+'.txt') and exists(path+'GD'+namel+'.txt'):
lt_hig = np.loadtxt(path+'HIG'+namet+'.txt')
ll_hig = np.loadtxt(path+'HIG'+namel+'.txt')
lt_sip = np.loadtxt(path+'SIP'+namet+'.txt')
ll_sip = np.loadtxt(path+'SIP'+namel+'.txt')
lt_gd = np.loadtxt(path+'GD'+namet+'.txt')
ll_gd = np.loadtxt(path+'GD'+namel+'.txt')
plt.plot(np.cumsum(lt_gd),ll_gd, label="GD")
plt.plot(np.cumsum(lt_sip),ll_sip, label="SIP")
plt.plot(np.cumsum(lt_hig),ll_hig, label="HIG")
plt.yscale('log')
plt.xlabel('Wall clock time [s]'); plt.ylabel('Training loss'); plt.legend()
plt.title('Linear chain comparison ')
plt.show()
else:
print("Run this notebook three times with MODE='HIG|SIP|GD' to produce the final graph")
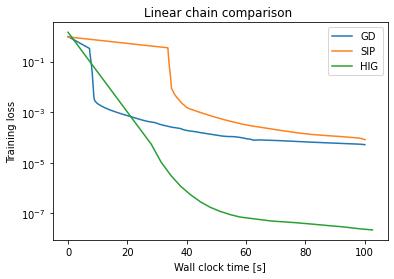
这个图表清晰地显示了收敛方面的显著差异:Adam(蓝色“GD”曲线)执行了大量的更新,但其对黑塞矩阵的粗略近似不足以收敛到高精度,它停滞在高损失水平上。
在这种情况下,SIP更新并没有超越Adam。这是由于相对简单的物理(线性振荡器)以及SIP更高的运行时成本所致。如果您在这个例子中运行得更久一些,SIP实际上会超过Adam,但开始受到完全反演的数值问题的影响。
HIGs的表现比另外两种方法要好得多:尽管每次迭代相对较慢,但半反演产生了非常好的更新,使得训练能够非常快速地收敛到非常低的损失值。HIGs达到的精度比其他两种方法高四个数量级左右。
22.7 下一步
这个笔记本有许多有趣的方向可以进行进一步的测试和修改:
- 最重要的是,到目前为止,我们实际上只看了训练表现!这使得笔记本保持了相对较短的长度,但这显然是不好的做法。虽然我们声称HIGs同样适用于_真实_测试数据,但这是使用这个笔记本的一个很好的下一步:分配适当的测试样本,并在测试数据上重新运行三种方法的评估。
- 此外,您可以改变物理行为:使用更多的振荡器来延长或缩短时间跨度,甚至包括非线性力(如HIG论文中所用)。请注意:对于后者,SIP版本将需要一个新的逆求解器。
在这一点上,现在是时候再退一步,评估迄今为止引入的不同方法。对于深度学习应用,我们可以广泛区分三种方法:常规可微物理(DP)训练,半逆梯度(HIGs)训练以及使用尺度不变的物理更新(SIPs)。不幸的是,我们不能简单地放弃其中两种方法,而将所有未来努力都集中在一种方法上。然而,讨论优缺点可以揭示物理基础深度学习的一些基本方面。

23.1 解决缩放问题
首先,改进更新的核心动机之一是解决学习问题的规模扩展问题。这并不是一个全新的问题:已经提出了许多深度学习算法来解决训练神经网络时的这些问题。然而,将神经网络与物理模拟相结合带来了新的挑战,同时也提供了解决这个问题的新角度。从负面方面来看,我们有来自PDE模型的额外非线性算子。从积极的方面来看,这些算子在学习过程中通常没有自由参数,因此可以用不同的定制方法处理。
这正是HIGs和SIPs的作用所在:它们不像其他神经网络一样处理物理模拟(这是DP方法),而是展示了使用定制的逆求解器(SIPs)或定制的数值逆转(HIGs)可以实现多大程度的训练尺度不变性。
23.2 计算资源
这两种情况通常导致更复杂和资源密集的训练。然而,假设在训练完成后我们可以多次重复使用已训练好的模型,在许多应用领域中,这样做往往能够迅速收回成本:尽管与其他训练方法获得的运行时相同,经过训练的神经网络通常能够显著提高准确性。使用常规的Adam和基于DP的训练方法很难达到类似的准确性水平。
当这样的训练好的神经网络被用作反问题的代理模型时,它可能会被大量执行,而提高的准确性可以在后续阶段节省大量的计算资源。一个很好的潜在例子是流体中浸泡体的阻力减小的形状优化 {cite}chen2021numerical。

23.3 总结
总之,本章展示了反演的重要性。一个重要的启示是,在涉及到偏微分方程时,神经网络训练的常规梯度并不是最佳选择。在这些情况下,我们可以获得比常规梯度提供的局部一阶信息更好的优化指导信息。
即使仅对物理模拟组件进行反演(如SIPs),也可以大大改善学习过程。自定义反演求解器允许我们在训练中使用更高阶的信息。
✅ 赞成 SIP:
- 对物理模拟提供非常准确的“梯度”信息。
- 通常可以显著改进收敛性和模型性能。
❌ 反对 SIP:
- 需要逆模拟器 (至少是局部的)。
- 仅使物理组件具有尺度不变性。
另一方面,HIGs回溯到雅可比形式的一阶信息。它们展示了即使没有任何高阶项,反演也可以有多么有用。同时,它们利用了神经网络和物理的组合反演,考虑了一个小批量样本的所有样本,计算出最优的一阶方向。
✅ 赞成 HIG:
- 针对物理模型和神经网络的扩展问题进行了强健处理。
- 改善了收敛性和模型性能。
❌ 反对 HIG:
- 需要对可能很大的雅可比矩阵进行奇异值分解(SVD)。
- 这在运行时间和内存方面可能代价高昂。
在这两种情况下,由此产生的神经网络可以获得我们通过更简单的差分隐私或监督方法训练更长时间无法获得的性能。因此,如果我们计划经常评估这些模型,例如在应用中使用它们,这种增加的一次性成本将在长期内得到回报。
这一章对基于物理的神经网络的改进学习方法进行了总结。这显然是一个活跃的研究领域,还有很多新方法的空间,但这里的算法已经表明了为物理问题量身定制的学习算法的潜力。这也结束了对数值模拟作为深度学习组件的关注。在下一章中,我们将转而关注一个不同的统计视角,即不确定性的包含。
我们应该牢记,在所有的测量、模型和离散化中,都存在着不确定性。对于测量和观测来说,这通常以测量误差的形式出现。而模型方程通常只包含我们感兴趣系统的部分(将其余部分作为不确定性),而对于数值模拟,我们本质上引入了离散化误差。因此,一个非常重要的问题是,我们如何确信我们得到的答案是正确的。从统计学家的角度来看,我们想知道后验概率分布,这是一个捕捉我们对模型或数据可能存在的不确定性的分布。
24.1 不确定性
在机器学习的背景下,这变得更加困难:我们通常面临着近似复杂和未知函数的任务。从概率的角度来看,训练神经网络的标准过程会产生网络参数的最大似然估计(MLE)。然而,这种MLE观点并没有考虑到上述任何不确定性:对于深度学习训练,我们同样有数值优化,因此存在学习表示的近似误差和不确定性。理想情况下,我们应该重新制定学习过程,使其考虑到自身的不确定性,并使后验推断成为可能,即学习如何产生完整的输出分布。然而,这被证明是一项极其困难的任务。
这就是所谓的贝叶斯神经网络(BNN)方法发挥作用的地方。它们通过对网络的各个参数的概率分布做出假设,允许进行后验推理。这给出了参数的分布,我们可以评估网络多次以获得不同版本的输出,并以此方式对输出的分布进行采样。
尽管如此,任务仍然非常具有挑战性。训练BNN通常比训练常规NN要困难得多。这并不奇怪,因为我们在这里试图学习的是根本不同的东西:完整的概率分布,而不是点估计。(所有之前的章节“只是”处理这样的点估计,而任务仍然远非微不足道。)
随机不确定性和认知不确定性
尽管本书不会详细介绍,但许多作品区分了两种不确定性,这里需要提到:
- Aleatoric 不确定性表示数据内部的不确定性,例如测量中的噪声。
- 另一方面,Epistemic 不确定性描述了模型内部的不确定性,例如训练的神经网络。
在接下来的内容中,我们将主要通过后验推断来研究 Epistemic 不确定性。但是,需要注意的是:如果它们一起出现,不同类型的不确定性(上述两种类型并不详尽)在实践中非常难以区分。

24.2 贝叶斯神经网络简介
为了将后验推断与神经网络相结合,我们可以使用贝叶斯建模中的标准技术,并将其与深度学习机制相结合。在贝叶斯建模中,我们的目标是学习模型参数的分布,而不是这些固定点估计。对于神经网络,模型参数是权重和偏置,由神经网络的总结。因此,我们的目标是从数据中学习所谓的后验分布,该分布捕捉我们在观察数据后对网络权重和偏置的不确定性。这个后验分布是这里的核心量:如果我们可以合理地估计它,我们可以用它来做出好的预测,但也可以评估与这些预测相关的不确定性。为了实现这两个目标,必须对后验分布进行边际化,即对其进行积分。例如,可以通过以下方式获得输入的单个预测:
同样地,可以计算标准差来评估对预测的不确定度度量。
24.3 先验分布
为了获得所需的后验分布,在贝叶斯建模中,首先必须定义一个先验分布,用于描述网络参数。这个先验分布应该包含我们在训练模型之前对网络权重的了解。例如,我们知道神经网络的权重通常非常小,可以是正数和负数。因此,中心正态分布是一个标准选择,具有一些小方差参数。为了计算简单起见,它们通常也被假定为彼此独立。当观察数据时,根据贝叶斯规则,权重的先验分布将被更新为后验分布:
这是我们在观察数据后更新先验知识的过程,即我们从数据中“学习”。贝叶斯更新所需的计算通常很复杂,特别是在处理复杂的网络结构时。因此,后验分布会被一个易于评估的变分分布近似,其中是参数化的。通常,对于每个权重,使用独立的正态分布。因此,参数包含这些正态分布的所有均值和方差参数。优化的目标是找到一个接近真实后验分布的分布。
评估这种接近程度的一种方法是KL散度,这是一种广泛应用于实践中用于衡量两个分布相似性的方法。
24.4 证据下界
我们无法直接最小化近似后验分布和真实后验分布之间的KL散度,因为我们无法获取真实后验分布。然而,可以证明我们可以等价地最大化所谓的证据下界(ELBO),这是一种在变分推断中广为人知的量:
ELBO(或负ELBO,如果更喜欢最小化而不是最大化)是BNN的优化目标。第一项是数据的期望对数似然。最大化它意味着尽可能好地解释数据。在实践中,对数似然通常是像均方误差这样的传统损失函数(注意,MSE可以被视为具有单位方差的正常噪声的负对数似然)。第二项是近似后验与先验之间的负KL散度。对于适当的先验和近似后验选择(例如上面的选择),可以通过解析方法计算这个项。最大化它意味着鼓励近似网络权重分布保持接近先验分布。从这个意义上讲,ELBO的两个术语具有相反的目标:第一个术语鼓励模型尽可能好地解释数据,而第二个术语鼓励模型保持接近(随机的)先验分布,这意味着随机性和正则化。
对数似然的期望通常无法以解析形式获得,但可以通过多种方式进行近似。例如,可以使用蒙特卡罗采样,并从中绘制个样本。然后通过来近似期望。在实践中,即使是单个样本,即也足够了。此外,对数似然的期望通常不是在整个数据集上评估的,而是通过数据批次进行近似,这使得可以使用批次随机梯度下降。
24.5 训练循环
当时,训练循环的一次迭代包括以下步骤:
- 抽取一个数据批次;
- 从中抽取网络权重和偏置;
- 根据抽取的权重将数据批次通过网络;
- 计算ELBO;
- 反向传播ELBO并更新。
如果,则需要重复步骤2和3 次以计算ELBO。从这个意义上讲,训练变分BNN与训练传统NN非常相似:我们仍然使用SGD和前向-后向传递来优化我们的损失函数。只是现在我们是在分布上进行优化,而不是单个值。如果您想知道如何通过分布进行反向传播,可以参考这里,并且在Y. Gals thesis的第2章和第3章中可以找到更详细的介绍贝叶斯神经网络。
24.5 替代方法Dropout
先前的研究表明,使用dropout等同于对概率深度高斯过程进行近似。此外,对于特定的先验条件(满足所谓的KL条件)和特定的近似后验选择(伯努利分布的乘积),使用dropout和L2正则化训练神经网络以及训练变分BNN会得到等效的优化过程。换句话说,dropout神经网络是贝叶斯神经网络的一种形式。
获得不确定性估计与训练传统神经网络并扩展dropout相当简单,而dropout通常仅在训练阶段使用,现在将其扩展到预测阶段。这将导致预测结果具有随机性(因为dropout会随机丢弃一些激活),从而使我们能够计算数据集中单个样本的平均值和标准差统计量,就像变分BNN的情况一样。
在学术界,关于变分方法和基于dropout的方法哪种更可取,仍存在持续的讨论。
24.6 一个实际例子
作为变分贝叶斯神经网络(Variational BNNs)后验推断的第一个真实示例,让我们重新审视一下空气动力学中的湍流绕流翼型案例,参考{doc}supervised-airfoils。然而,与本节中学习的点估计不同,我们现在的目标是学习完整的后验分布。
25.1 概述
我们正在考虑与笔记本《监督型机翼》中相同的设置:研究翼型周围的湍流气流,希望了解在不同雷诺数和攻角下的平均运动和压力分布。在早期的笔记本中,我们通过完全绕过任何物理求解器,而是训练一个神经网络来学习感兴趣的量来解决这个问题。现在,我们想将这种方法扩展到前一节中的变分贝叶斯神经网络(BNNs)。与传统网络不同,传统网络为每个权重值学习一个单点估计值,而BNNs的目标是学习每个权重参数上的分布(例如,具有均值和方差的高斯分布)。在前向传递过程中,网络中的每个参数都从相应的近似后验分布中抽样。从这个意义上讲,网络参数本身是随机变量,每次前向传递都是随机的,因为对于给定的输入,预测结果会在每次前向传递中变化。这可以用来评估网络的“不确定性”:如果预测结果变化很大,我们认为网络对其输出结果不确定。
[在colab中运行] ( https://colab.research.google.com/github/tum-pbs/pbdl-book/blob/main/bayesian-code.ipynb )
25.1.1 读取数据
与之前的笔记本一样,我们将跳过数据生成过程。这个示例改编自Deep-Flow-Prediction代码库,您可以查看详细信息。在这里,我们将简单地下载一小部分使用OpenFOAM中的Spalart-Almaras RANS模拟生成的训练数据。
import numpy as np
import os.path, random
# get training data: as in the previous supervised example, either download or use gdrive
dir = "./"
if True:
if not os.path.isfile('data-airfoils.npz'):
import requests
print("Downloading training data (300MB), this can take a few minutes the first time...")
with open("data-airfoils.npz", 'wb') as datafile:
resp = requests.get('https://dataserv.ub.tum.de/s/m1615239/download?path=%2F&files=dfp-data-400.npz', verify=False)
datafile.write(resp.content)
else: # cf supervised airfoil code:
from google.colab import drive
drive.mount('/content/gdrive')
dir = "./gdrive/My Drive/"
npfile=np.load(dir+'data-airfoils.npz')
print("Loaded data, {} training, {} validation samples".format(len(npfile["inputs"]),len(npfile["vinputs"])))
print("Size of the inputs array: "+format(npfile["inputs"].shape))
# reshape to channels_last for convencience
X_train = np.moveaxis(npfile["inputs"],1,-1)
y_train = np.moveaxis(npfile["targets"],1,-1)
X_val = np.moveaxis(npfile["vinputs"],1,-1)
y_val = np.moveaxis(npfile["vtargets"],1,-1)
Downloading training data (300MB), this can take a few minutes the first time...
Loaded data, 320 training, 80 validation samples
Size of the inputs array: (320, 3, 128, 128)
25.1.2 查看数据
现在我们有一些训练数据。我们可以使用在原始笔记本中所用的代码来查看它。
import pylab
from matplotlib import cm
# helper to show three target channels: normalized, with colormap, side by side
def showSbs(a1,a2, bottom="NN Output", top="Reference", title=None):
c=[]
for i in range(3):
b = np.flipud( np.concatenate((a2[...,i],a1[...,i]),axis=1).transpose())
min, mean, max = np.min(b), np.mean(b), np.max(b);
b -= min; b /= (max-min)
c.append(b)
fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
axes.set_xticks([]); axes.set_yticks([]);
im = axes.imshow(np.concatenate(c,axis=1), origin='upper', cmap='magma')
pylab.colorbar(im); pylab.xlabel('p, ux, uy'); pylab.ylabel('%s %s'%(bottom,top))
if title is not None: pylab.title(title)
NUM=40
print("\nHere are all 3 inputs are shown at the top (mask,in x, in y) \nSide by side with the 3 output channels (p,vx,vy) at the bottom:")
showSbs( X_train[NUM],y_train[NUM], bottom="Target Output", top="Inputs", title="Training data sample")
Here are all 3 inputs are shown at the top (mask,in x, in y)
Side by side with the 3 output channels (p,vx,vy) at the bottom:

不出所料, 数据看起来仍然相同。有关详细信息, 请查看{doc} supervised-airfoils 中的描述。
25.1.3 神经网络定义
现在让我们来看看如何实现BNNs(贝叶斯神经网络)。与PyTorch不同,我们将使用TensorFlow,特别是TensorFlow Probability扩展,它具有易于实现的概率层。与另一个笔记本类似,我们使用一个由具有跳跃连接的卷积块组成的U-Net结构。目前,我们只想将解码器设置为贝叶斯部分,也就是U-Net的第二部分。为此,我们将利用TensorFlow的flipout层(特别是卷积实现)。
在前向传播中,这些层会自动从当前后验分布中进行采样,并将先验与后验之间的KL散度存储在_model.losses_中。如果希望使用非正态分布以外的其他先验和近似后验分布,可以指定所需的散度度量(通常是KL散度)并进行修改。除此之外,flipout层可以像顺序结构中的常规层一样使用。下面的代码实现了U-Net的单个卷积块:
import tensorflow as tf
import tensorflow_probability.python.distributions as tfd
from tensorflow.keras import Sequential
from tensorflow.keras.initializers import RandomNormal
from tensorflow.keras.layers import Input, Conv2D, Conv2DTranspose,UpSampling2D, BatchNormalization, ReLU, LeakyReLU, SpatialDropout2D, MaxPooling2D
from tensorflow_probability.python.layers import Convolution2DFlipout
from tensorflow.keras.models import Model
def tfBlockUnet(filters=3, transposed=False, kernel_size=4, bn=True, relu=True, pad="same", dropout=0., flipout=False,
kdf=None, name=''):
block = Sequential(name=name)
if relu:
block.add(ReLU())
else:
block.add(LeakyReLU(0.2))
if not transposed:
block.add(Conv2D(filters=filters, kernel_size=kernel_size, padding=pad,
kernel_initializer=RandomNormal(0.0, 0.02), activation=None,strides=(2,2)))
else:
block.add(UpSampling2D(interpolation = 'bilinear'))
if flipout:
block.add(Convolution2DFlipout(filters=filters, kernel_size=(kernel_size-1), strides=(1, 1), padding=pad,
data_format="channels_last", kernel_divergence_fn=kdf,
activation=None))
else:
block.add(Conv2D(filters=filters, kernel_size=(kernel_size-1), padding=pad,
kernel_initializer=RandomNormal(0.0, 0.02), strides=(1,1), activation=None))
block.add(SpatialDropout2D(rate=dropout))
if bn:
block.add(BatchNormalization(axis=-1, epsilon=1e-05,momentum=0.9))
return block
接下来,我们使用这些模块定义完整的网络结构,其结构与之前的笔记本几乎完全相同。我们手动定义了名为kdf的核散度函数,并用一个名为kl_scaling的因子对其进行了缩放。这样做有两个原因:
首先,如果我们要使用正确的损失(如在{doc}bayesian-intro中介绍的),我们应该每个周期只应用一次KL散度。由于我们将使用基于批次的训练,因此需要将KL散度按批次数量进行缩放,以便在每次参数更新中,只有kdf / num_batches被添加到损失中。在一个周期内,会执行num_batches次参数更新,并使用“完整的”KL散度。这个批次缩放值通过在稍后实例化Bayes_DfpNet 神经网络时,通过kl_scaling传递给网络初始化。
其次,通过调整损失函数中的KL散度部分的比例,我们可以调整网络中允许的随机性程度:如果完全忽略KL散度,我们将只是最小化常规损失(例如MSE或MAE),就像在传统神经网络中一样。如果我们忽略负对数似然,我们将优化网络,以便从先验分布中获得随机抽样。通过对KL散度的缩放进行平衡,可以调整这些极端情况,但实践中很困难。
def Bayes_DfpNet(input_shape=(128,128,3),expo=5,dropout=0.,flipout=False,kl_scaling=10000):
channels = int(2 ** expo + 0.5)
kdf = (lambda q, p, _: tfd.kl_divergence(q, p) / tf.cast(kl_scaling, dtype=tf.float32))
layer1=Sequential(name='layer1')
layer1.add(Conv2D(filters=channels,kernel_size=4,strides=(2,2),padding='same',activation=None,data_format='channels_last'))
layer2=tfBlockUnet(filters=channels*2,transposed=False,bn=True, relu=False,dropout=dropout,name='layer2')
layer3=tfBlockUnet(filters=channels*2,transposed=False,bn=True, relu=False,dropout=dropout,name='layer3')
layer4=tfBlockUnet(filters=channels*4,transposed=False,bn=True, relu=False,dropout=dropout,name='layer4')
layer5=tfBlockUnet(filters=channels*8,transposed=False,bn=True, relu=False,dropout=dropout,name='layer5')
layer6=tfBlockUnet(filters=channels*8,transposed=False,bn=True, relu=False,dropout=dropout,kernel_size=2,pad='valid',name='layer6')
layer7=tfBlockUnet(filters=channels*8,transposed=False,bn=True, relu=False,dropout=dropout,kernel_size=2,pad='valid',name='layer7')
# note, kernel size is internally reduced by one for the decoder part
dlayer7=tfBlockUnet(filters=channels*8,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf, kernel_size=2,pad='valid',name='dlayer7')
dlayer6=tfBlockUnet(filters=channels*8,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf, kernel_size=2,pad='valid',name='dlayer6')
dlayer5=tfBlockUnet(filters=channels*4,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer5')
dlayer4=tfBlockUnet(filters=channels*2,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer4')
dlayer3=tfBlockUnet(filters=channels*2,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer3')
dlayer2=tfBlockUnet(filters=channels ,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer2')
dlayer1=Sequential(name='outlayer')
dlayer1.add(ReLU())
dlayer1.add(Conv2DTranspose(3,kernel_size=4,strides=(2,2),padding='same'))
# forward pass
inputs=Input(input_shape)
out1 = layer1(inputs)
out2 = layer2(out1)
out3 = layer3(out2)
out4 = layer4(out3)
out5 = layer5(out4)
out6 = layer6(out5)
out7 = layer7(out6)
# ... bottleneck ...
dout6 = dlayer7(out7)
dout6_out6 = tf.concat([dout6,out6],axis=3)
dout6 = dlayer6(dout6_out6)
dout6_out5 = tf.concat([dout6, out5], axis=3)
dout5 = dlayer5(dout6_out5)
dout5_out4 = tf.concat([dout5, out4], axis=3)
dout4 = dlayer4(dout5_out4)
dout4_out3 = tf.concat([dout4, out3], axis=3)
dout3 = dlayer3(dout4_out3)
dout3_out2 = tf.concat([dout3, out2], axis=3)
dout2 = dlayer2(dout3_out2)
dout2_out1 = tf.concat([dout2, out1], axis=3)
dout1 = dlayer1(dout2_out1)
return Model(inputs=inputs,outputs=dout1)
让我们定义超参数并创建一个 TensorFlow 数据集来组织输入和目标。由于训练集中有 320 个观测值,对于批次大小为 10,我们应该将 KL 散度按比例缩放为 320/10=32,以便每个周期只应用一次完整的 KL 散度。此外,我们还将通过一个名为 KL_PREF=5000 的因子进一步将 KL 散度缩小,该因子在实践中已经被证明效果良好。
此外,我们将定义一个实现学习率衰减的函数。直观地说,这使得优化在后续epoch中更精确(通过更小的步长),同时在前几个epoch中仍然能够快速进展(通过更大的步长)。
import math
import matplotlib.pyplot as plt
BATCH_SIZE=10
LR=0.001
EPOCHS = 120
KL_PREF = 5000
dataset = tf.data.Dataset.from_tensor_slices((X_train, y_train)).shuffle(len(X_train),
seed=46168531, reshuffle_each_iteration=False).batch(BATCH_SIZE, drop_remainder=False)
def compute_lr(i, epochs, minLR, maxLR):
if i < epochs * 0.5:
return maxLR
e = (i / float(epochs) - 0.5) * 2.
# rescale second half to min/max range
fmin = 0.
fmax = 6.
e = fmin + e * (fmax - fmin)
f = math.pow(0.5, e)
return minLR + (maxLR - minLR) * f
我们可以可视化学习率衰减:我们从一个恒定的学习率开始,在 EPOCHS 的一半之后,我们开始指数衰减学习率,直到达到原始学习率的一半。
lrs=[compute_lr(i, EPOCHS, 0.5*LR,LR) for i in range(EPOCHS)]
plt.plot(lrs)
plt.xlabel('Iteration')
plt.ylabel('Learning Rate')
让我们初始化网络。在这里, 我们最终通过 KL_PREF 和批量大小计算 kl_scaling 因子。
from tensorflow.keras.optimizers import RMSprop, Adam
model=Bayes_DfpNet(expo=4,flipout=True,kl_scaling=KL_PREF*len(X_train)/BATCH_SIZE)
optimizer = Adam(learning_rate=LR, beta_1=0.5,beta_2=0.9999)
num_params = np.sum([np.prod(v.get_shape().as_list()) for v in model.trainable_variables])
print('The Bayesian U-Net has {} parameters.'.format(num_params))
一般来说,与其传统对应物相比,翻转层的参数是两倍,因为不仅需要学习高斯后验权重的均值和方差参数,还需要学习单点估计。由于这里我们只对解码器部分使用了翻转层, 生成的模型具有 846787 个参数,而传统 NN 具有 585667 个参数。
25.2 训练
现在我们准备开始训练!请注意,这可能需要一些时间(通常约为4小时),因为与常规层相比,翻转层的训练速度较慢。
from tensorflow.keras.losses import mae
import math
kl_losses=[]
mae_losses=[]
total_losses=[]
mae_losses_vali=[]
for epoch in range(EPOCHS):
# compute learning rate - decay is implemented
currLr = compute_lr(epoch,EPOCHS,0.5*LR,LR)
if currLr < LR:
tf.keras.backend.set_value(optimizer.lr, currLr)
# iterate through training data
kl_sum = 0
mae_sum = 0
total_sum=0
for i, traindata in enumerate(dataset, 0):
# forward pass and loss computation
with tf.GradientTape() as tape:
inputs, targets = traindata
prediction = model(inputs, training=True)
loss_mae = tf.reduce_mean(mae(prediction, targets))
kl=sum(model.losses)
loss_value=kl+tf.cast(loss_mae, dtype='float32')
# backpropagate gradients and update parameters
gradients = tape.gradient(loss_value, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
# store losses per batch
kl_sum += kl
mae_sum += tf.reduce_mean(loss_mae)
total_sum+=tf.reduce_mean(loss_value)
# store losses per epoch
kl_losses+=[kl_sum/len(dataset)]
mae_losses+=[mae_sum/len(dataset)]
total_losses+=[total_sum/len(dataset)]
# validation
outputs = model.predict(X_val)
mae_losses_vali += [tf.reduce_mean(mae(y_val, outputs))]
if epoch<3 or epoch%20==0:
print('Epoch {}/{}, total loss: {:.3f}, KL loss: {:.3f}, MAE loss: {:.4f}, MAE loss vali: {:.4f}'.format(epoch, EPOCHS, total_losses[-1], kl_losses[-1], mae_losses[-1], mae_losses_vali[-1]))
Epoch 0/120, total loss: 4.265, KL loss: 4.118, MAE loss: 0.1464, MAE loss vali: 0.0872
Epoch 1/120, total loss: 4.159, KL loss: 4.089, MAE loss: 0.0706, MAE loss vali: 0.0691
Epoch 2/120, total loss: 4.115, KL loss: 4.054, MAE loss: 0.0610, MAE loss vali: 0.0589
Epoch 20/120, total loss: 3.344, KL loss: 3.315, MAE loss: 0.0291, MAE loss vali: 0.0271
Epoch 40/120, total loss: 2.495, KL loss: 2.471, MAE loss: 0.0245, MAE loss vali: 0.0242
Epoch 60/120, total loss: 1.712, KL loss: 1.689, MAE loss: 0.0228, MAE loss vali: 0.0208
Epoch 80/120, total loss: 1.190, KL loss: 1.169, MAE loss: 0.0212, MAE loss vali: 0.0200
Epoch 100/120, total loss: 0.869, KL loss: 0.848, MAE loss: 0.0208, MAE loss vali: 0.0203
BNN已经训练完毕!让我们来看一下损失。由于损失由两个独立的部分组成,监控这两个部分(MAE和KL)是很有帮助的。
fig,axs=plt.subplots(ncols=3,nrows=1,figsize=(20,4))
axs[0].plot(kl_losses,color='red')
axs[0].set_title('KL Loss (Train)')
axs[1].plot(mae_losses,color='blue',label='train')
axs[1].plot(mae_losses_vali,color='green',label='val')
axs[1].set_title('MAE Loss'); axs[1].legend()
axs[2].plot(total_losses,label='Total',color='black')
axs[2].plot(kl_losses,label='KL',color='red')
axs[2].plot(mae_losses,label='MAE',color='blue')
axs[2].set_title('Total Train Loss'); axs[2].legend()
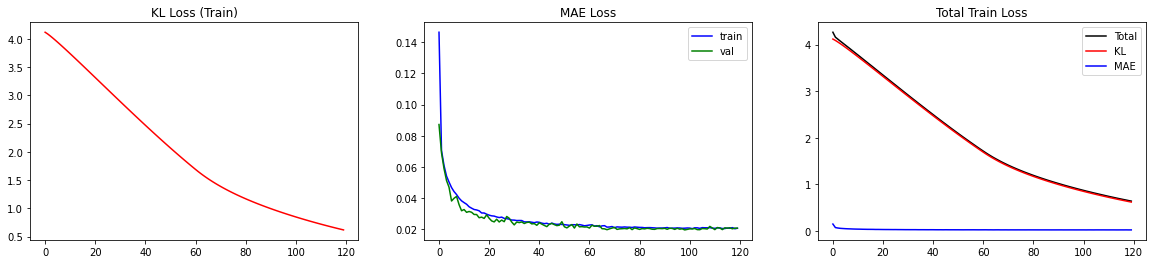
这样,我们可以进行双重检查,以确定减小损失的一个部分是否以增加另一个部分为代价。对于我们的情况,我们观察到两个部分都在平稳下降。特别是,MAE损失对于验证集而言并没有增加,这表明我们没有过拟合。
双重检查添加了多少层KL损失是一个好的实践。我们可以检查_model.losses来了解。由于解码器由6个连续块和flipout层组成,我们预计_model.losses中会有6个条目。
# there should be 6 entries in model.losses since we have 6 blocks with flipout layers in our model
print('There are {} entries in model.losses'.format(len(model.losses)))
print(model.losses)
There are 6 entries in model.losses
[<tf.Tensor: shape=(), dtype=float32, numpy=0.03536303>, <tf.Tensor: shape=(), dtype=float32, numpy=0.06506929>, <tf.Tensor: shape=(), dtype=float32, numpy=0.2647468>, <tf.Tensor: shape=(), dtype=float32, numpy=0.09337218>, <tf.Tensor: shape=(), dtype=float32, numpy=0.0795429>, <tf.Tensor: shape=(), dtype=float32, numpy=0.075103864>]
现在让我们来可视化一下BNN在验证集中的未知数据上的性能。理想情况下,我们希望将参数积分掉,即进行边缘化以获得预测结果。由于这在分析上很难实现,通常会通过从后验中进行采样来近似积分:
在实践中,这意味着对于每个输入,执行次前向传递,并计算平均值,其中每个是从中抽取的。以同样的精神,可以通过标准差来衡量不确定性:
请注意,和仍然具有形状,即均值和方差计算是按像素进行的(但可能在之后聚合为全局度量)。
REPS=20
preds=np.zeros(shape=(REPS,)+X_val.shape)
for rep in range(REPS):
preds[rep,:,:,:,:]=model.predict(X_val)
preds_mean=np.mean(preds,axis=0)
preds_std=np.std(preds,axis=0)
在检查前一个单元格中计算出的平均值和标准偏差之前,让我们可视化BNN的一个输出。在下面的图中,第一行显示输入,而第二行说明单次前向传递的结果。
NUM=16
# show a single prediction
showSbs(y_val[NUM],preds[0][NUM], top="Inputs", bottom="Single forward pass")
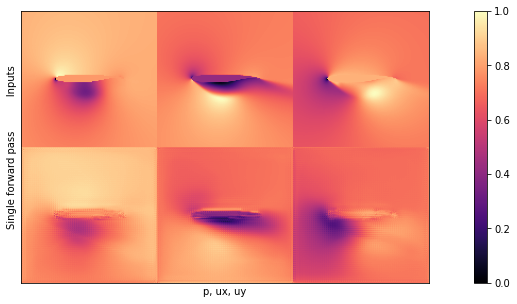
如果你将这个图像与{doc}supervised-airfoils中的输出进行比较,你会发现乍一看它们并没有太大的区别。这是一个好兆头,似乎网络已经学会了生成压力和速度场的内容。
然而,更重要的是,我们现在可以通过检查后验分布中的几个样本以及给定输入的标准差,更清楚地可视化预测的不确定性。下面是一个用于准确可视化的函数代码(为了突出与之前的非贝叶斯笔记本的差异,不确定性使用了不同的颜色映射)。
# plot repeated samples from posterior for some observations
def plot_BNN_predictions(target, preds, pred_mean, pred_std, num_preds=5,channel=0):
if num_preds>len(preds):
print('num_preds was set to {}, but has to be smaller than the length of preds. Setting it to {}'.format(num_preds,len(preds)))
num_preds = len(preds)
# transpose and concatenate the frames that are to plot
to_plot=np.concatenate((target[:,:,channel].transpose().reshape(128,128,1),preds[0:num_preds,:,:,channel].transpose(),
pred_mean[:,:,channel].transpose().reshape(128,128,1),pred_std[:,:,channel].transpose().reshape(128,128,1)),axis=-1)
fig, axs = plt.subplots(nrows=1,ncols=to_plot.shape[-1],figsize=(20,4))
for i in range(to_plot.shape[-1]):
label='Target' if i==0 else ('Avg Pred' if i == (num_preds+1) else ('Std Dev (normalized)' if i == (num_preds+2) else 'Pred {}'.format(i)))
colmap = cm.viridis if i==to_plot.shape[-1]-1 else cm.magma
frame = np.flipud(to_plot[:,:,i])
min=np.min(frame); max = np.max(frame)
frame -= min; frame /=(max-min)
axs[i].imshow(frame,cmap=colmap)
axs[i].axis('off')
axs[i].set_title(label)
OBS_IDX=5
plot_BNN_predictions(y_val[OBS_IDX,...],preds[:,OBS_IDX,:,:,:],preds_mean[OBS_IDX,...],preds_std[OBS_IDX,...])

我们正在查看通道0,也就是压力。可以观察到在不同的预测中,暗区和亮区变化相当大。令人欣慰的是,至少从视觉检查来看,平均(边缘)预测比大多数单次正向传递更接近目标。
还需要注意的是,每个帧都经过了归一化处理以进行可视化。因此,当观察不确定性帧时,我们可以推断出网络在哪些地方不确定,但不能确定其绝对值的不确定程度。为了评估不确定性的全局度量,我们可以计算验证集中所有样本的平均标准差。
# Average Prediction with total uncertainty
uncertainty_total = np.mean(np.abs(preds_std),axis=(0,1,2))
preds_mean_global = np.mean(np.abs(preds),axis=(0,1,2,3))
print("\nAverage pixel prediction on validation set: \n pressure: {} +- {}, \n ux: {} +- {},\n uy: {} +- {}".format(np.round(preds_mean_global[0],3),np.round(uncertainty_total[0],3),np.round(preds_mean_global[1],3),np.round(uncertainty_total[1],3),np.round(preds_mean_global[2],3),np.round(uncertainty_total[2],3)))
Average pixel prediction on validation set:
pressure: 0.025 +- 0.009,
ux: 0.471 +- 0.019,
uy: 0.081 +- 0.016
对于使用标准设置的运行,三个场的不确定性大约在0.01的数量级上。由于压力场的均值较小,相对而言其不确定性更大。这是有道理的,因为众所周知,压力场比两个速度分量更难预测。
25.3 测试评估
就像对于传统神经网络一样,现在让我们来看一下合适的测试样本,也就是OOD样本,对于这些样本,我们将使用新的翼型。这些翼型是网络在任何训练样本中都没有见过的,因此它可以告诉我们网络对新形状的泛化能力如何。
由于这些样本至少在某种程度上属于OOD,我们可以得出关于网络泛化能力的结论,而这是验证数据无法告诉我们的。特别是,我们想要调查神经网络在处理OOD数据时是否更加不确定。与之前一样,我们首先下载测试样本...
if not os.path.isfile('data-airfoils-test.npz'):
import urllib.request
url="https://physicsbaseddeeplearning.org/data/data_test.npz"
print("Downloading test data, this should be fast...")
urllib.request.urlretrieve(url, 'data-airfoils-test.npz')
nptfile=np.load('data-airfoils-test.npz')
print("Loaded {}/{} test samples".format(len(nptfile["test_inputs"]),len(nptfile["test_targets"])))
Downloading test data, this should be fast...
Loaded 10/10 test samples
...然后重复上述步骤,对测试样本进行BNN评估,并计算边缘化的预测和不确定性。
X_test = np.moveaxis(nptfile["test_inputs"],1,-1)
y_test = np.moveaxis(nptfile["test_targets"],1,-1)
REPS=10
preds_test=np.zeros(shape=(REPS,)+X_test.shape)
for rep in range(REPS):
preds_test[rep,:,:,:,:]=model.predict(X_test)
preds_test_mean=np.mean(preds_test,axis=0)
preds_test_std=np.std(preds_test,axis=0)
test_loss = tf.reduce_mean(mae(preds_test_mean, y_test))
print("\nAverage test error: {}".format(test_loss))
Average test error: 0.023046530292471824
# Average Prediction with total uncertainty
uncertainty_test_total = np.mean(np.abs(preds_test_std),axis=(0,1,2))
preds_test_mean_global = np.mean(np.abs(preds_test),axis=(0,1,2,3))
print("\nAverage pixel prediction on test set: \n pressure: {} +- {}, \n ux: {} +- {},\n uy: {} +- {}".format(np.round(preds_test_mean_global[0],3),np.round(uncertainty_test_total[0],3),np.round(preds_test_mean_global[1],3),np.round(uncertainty_test_total[1],3),np.round(preds_test_mean_global[2],3),np.round(uncertainty_test_total[2],3)))
Average pixel prediction on test set:
pressure: 0.03 +- 0.012,
ux: 0.466 +- 0.024,
uy: 0.091 +- 0.02
这是令人欣慰的:在具有新形状的OOD测试集上,不确定性至少略高于验证集。
25.3.1 可视化
下面的图表可视化了这些度量结果:它将验证集和测试集的平均绝对误差并排显示,同时使用误差线表示预测的不确定性:
# plot per channel MAE with uncertainty
val_loss_c, test_loss_c = [], []
for channel in range(3):
val_loss_c.append( tf.reduce_mean(mae(preds_mean[...,channel], y_val[...,channel])) )
test_loss_c.append( tf.reduce_mean(mae(preds_test_mean[...,channel], y_test[...,channel])) )
fig, ax = plt.subplots()
ind = np.arange(len(val_loss_c)); width=0.3
bars1 = ax.bar(ind - width/2, val_loss_c, width, yerr=uncertainty_total, capsize=4, label="validation")
bars2 = ax.bar(ind + width/2, test_loss_c, width, yerr=uncertainty_test_total, capsize=4, label="test")
ax.set_ylabel("MAE & Uncertainty")
ax.set_xticks(ind); ax.set_xticklabels(('P', 'u_x', 'u_y'))
ax.legend(); plt.tight_layout()
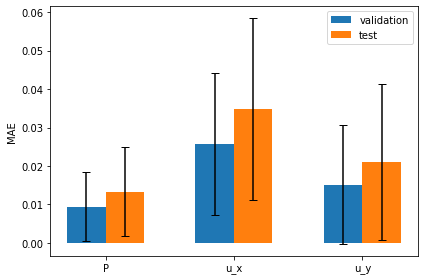
平均误差显然更大,而预测的稍大不确定性也通过误差线呈现出来。
一般来说,获得校准的不确定性估计是困难的,但由于我们处理的是一个相当简单的问题,BNN能够相当好地估计不确定性。
下一个图表展示了测试集中单个案例的BNN预测差异(使用与上述验证样本相同的样式):
OBS_IDX=5
plot_BNN_predictions(y_test[OBS_IDX,...],preds_test[:,OBS_IDX,:,:,:],preds_test_mean[OBS_IDX,...],preds_test_std[OBS_IDX,...])
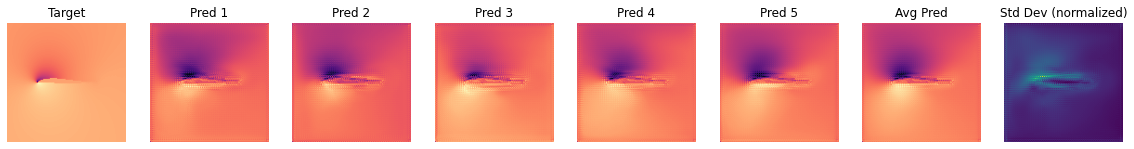
我们还可以将测试集中的几个形状与相应的边缘化预测和不确定性一起进行可视化。
IDXS = [1,3,8]
CHANNEL = 0
fig, axs = plt.subplots(nrows=len(IDXS),ncols=3,sharex=True, sharey = True, figsize = (9,len(IDXS)*3))
for i, idx in enumerate(IDXS):
axs[i][0].imshow(np.flipud(X_test[idx,:,:,CHANNEL].transpose()), cmap=cm.magma)
axs[i][1].imshow(np.flipud(preds_test_mean[idx,:,:,CHANNEL].transpose()), cmap=cm.magma)
axs[i][2].imshow(np.flipud(preds_test_std[idx,:,:,CHANNEL].transpose()), cmap=cm.viridis)
axs[0][0].set_title('Shape')
axs[0][1].set_title('Avg Pred')
axs[0][2].set_title('Std. Dev')
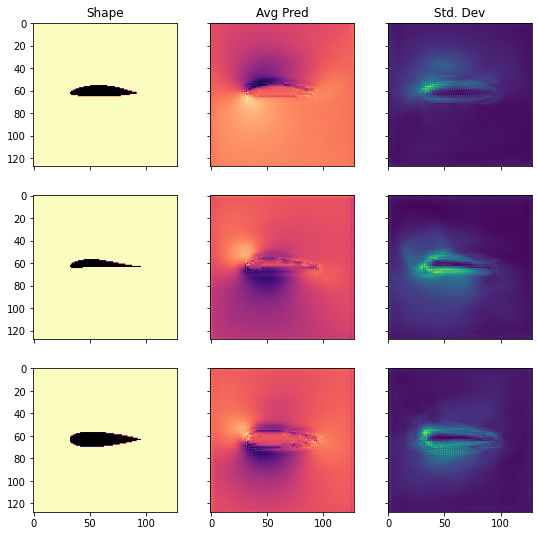
正如我们所看到的,测试集中的形状彼此之间有很大的差异。然而,不确定性估计相对合理地分布。它在翼型周围的边界层和低压区域尤为明显。
25.3.2 讨论
尽管这些结果令人鼓舞,贝叶斯神经网络仍存在一些问题,限制了它们在许多实际应用中的使用。其中一个严重的缺点是需要对KL损失进行额外的缩放,而且目前还没有令人信服的理由说明为什么这是必要的(详见这里 或 这里)。
此外,一些人认为将独立正态分布作为后验的变分近似是一种过度简化,因为在实践中,权重实际上是高度相关的(参考论文)。而其他一些人则认为,只要使用的网络足够深,这可能并不是一个问题(参考论文)。此外,还有关于BNN的许多其他方面的研究,例如使用不同的先验(如重尾分布)等。
25.4 下一步
现在是时候自己进行贝叶斯神经网络的实验了。
-
一个有趣的方面是观察我们的贝叶斯神经网络在调整KL预乘因子后的行为变化。在上面的训练循环中,我们将其设置为5000,但没有进一步的理由解释。你可以尝试使用理论建议的值1来替代5000,看看会发生什么变化。根据我们的实现,这样做应该使网络更具"贝叶斯"特性,因为我们赋予KL散度更大的重要性。
-
到目前为止,我们只使用了通过TensorFlow概率层来实现的变分贝叶斯神经网络。回想一下,还有一种更简单的方法来获得不确定性估计:不仅在训练时使用dropout,而且在推断时也使用dropout。你可以观察一下在这种情况下输出的变化。为了实现这个,你可以在网络规范中设置一个非零的dropout率,并将上面的预测阶段从_model.predict(...)更改为_model(..., training=True)。设置_training=True标志将告诉TensorFlow将输入视为训练数据,因此会应用dropout。请注意,training=True标志也会影响网络的其他特性。例如,批归一化在训练和预测模式下的工作方式是不同的。只要我们处理的数据差异不大,并且使用足够大的批量大小,这不会引入较大的误差。开始尝试的合理dropout率可能在0.1左右。
接下来的部分将简要介绍与基于物理的深度学习相关的其他高度有趣的主题。这些主题(目前)没有附带可执行的笔记本,但我们仍然会提到每个主题的现有开源实现。

具体而言,我们将关注以下内容:
-
模型简化和时间序列预测,即使用深度学习在潜在空间中预测物理系统的演化。这通常取代了数值求解器,并且我们可以利用深度学习领域的特殊技术来处理时间序列。
-
生成模型在深度学习中也是一个独立的主题,特别是生成对抗网络已被证明是强大的工具。它们还代表了一种涉及分离神经网络的高度有趣的训练方法。
-
无网格方法和非结构化网格是经典模拟的重要主题。在这里,我们将介绍一种特定的拉格朗日方法,它在动态的、基于粒子的表示的背景下应用了学习。
-
最后,用于可靠评估测量和结果相似性质量的指标是所有数值方法的核心主题,无论它们是否使用学习。在最后一节中,我们将看看如何使用深度学习来学习专门的和改进的度量方法。{cite}
kohl2020lsim
对于许多实际的偏微分方程求解器来说,一个固有的挑战是问题的高维性。对于一个三维问题(其中表示每个轴上的样本数),我们的模型通常以的样本进行离散化,对于时变现象,我们还需要在时间上进行离散化。后者的规模通常与空间维度成比例。这总共导致了数量级的样本数量。毫不奇怪,在这些情况下,随着的增大(对于所有实际的高保真应用,我们希望尽可能大),工作量迅速增加。
降低复杂性的一种流行方法是将系统的空间状态映射到一个更低维的状态,其中。在这个潜在空间中,我们通过推断新状态来估计系统的演化,然后解码以获得。为了使这个方法奏效,关键是我们可以选择足够大的来捕捉解集中的所有重要结构,并且能够高效计算的时间预测,以便尽管有额外的编码和解码步骤,仍然能够提高性能。在实践中,常规模拟中未知数的爆炸增长(上述的)以及直接计算新状态的超线性复杂度使得这种方法非常昂贵,而使用潜在空间点很快就能在较小的上收到回报。
然而,编码器和解码器在降低问题维度方面的表现非常重要。这对于深度学习方法来说是一个非常好的任务。此外,我们还需要对潜在空间状态进行时间演化,而对于大多数实际的模型方程,我们无法找到闭合形式的解来演化。因此,这同样对深度学习提出了一个非常好的问题。总结一下,我们面临着两个挑战:学习良好的空间编码和解码,以及学习准确的时间演化。
在下面,我们将描述一种解决这个问题的方法,该方法遵循Wiewel等人的方法{cite}wiewel2019lss和{cite}wiewel2020lsssubdiv,而这些方法又采用了Kim等人的编码器/解码器{cite}bkim2019deep。
27.1 降阶模型
减少计算模型的维度和复杂性,通常被称为“降阶建模”(ROM)或“模型简化”,是计算领域的一个经典主题。传统技术通常使用主成分分析等技术来得到所选解空间的基础。然而,由于构造上的线性特性,这些方法在表示复杂的非线性解集时存在固有的局限性。在实践中,所有“有趣”的解都是高度非线性的,因此深度学习作为学习非线性表示的一种方法引起了相当大的关注。由于非线性性质,与传统方法相比,深度学习表示在降阶模型中可以以较少的自由度实现较高的精度。
用于降阶模型的经典神经网络是一个“自编码器”。这表示一个网络的唯一任务是在经过位于或接近神经网络层堆栈中间的瓶颈时重构给定的输入。瓶颈处的数据表示压缩的潜在空间表示。通往瓶颈的网络部分是编码器,而瓶颈之后的部分是解码器。结合起来,学习任务可以写成:
通过编码器(权重为)和解码器(权重为),我们可以实现这个学习目标。对于这个学习目标,我们只需要,不需要其他任何数据,因为它们既代表输入又代表参考输出。
自编码器网络通常由卷积层堆叠而成。虽然这些层的细节可以灵活选择,但所有自编码器架构的一个关键属性是编码器和解码器之间不能存在连接。因此,网络必须能够分离编码器和解码器。
这是合理的,因为编码器和解码器之间的任何连接(或信息共享)都将阻止以独立的方式使用编码器或解码器。例如,解码器必须能够仅通过潜在空间点来纯粹解码完整状态。
27.1.1 自动编码器变体
这里值得一提的是自编码器的一个受欢迎的变种:所谓的“变分自编码器”(Variational Autoencoders,简称VAEs)。这些自编码器遵循上述的结构,但额外采用了一个损失项来塑造潜在空间。其目标是让潜在空间遵循已知的分布。这使得在潜在空间中能够直接绘制样本,无需采取额外步骤,比如将样本投影到潜在空间中。
通常,我们使用正态分布作为目标,使得潜在空间成为一个维的单位立方体:每个维度应具有零均值和单位标准差。这种方法在解码器需要用作生成模型时特别有用。例如,我们可以直接生成样本,并对其进行解码以获取完整的状态。虽然这在构建人脸或其他类型的自然图像的生成模型等应用中非常有用,但在模拟环境中并不是非常关键。在这里,我们希望获得一个能够促进时间预测的潜在空间,而不是能够轻松从中生成样本。
27.2 时间序列
时间预测的目标是根据一个或多个先前的潜在空间状态,在时间计算出一个潜在空间状态。最直接的方式是形式化对应的最小化问题,
其中预测网络被表示为,以区别于上述的编码器和解码器。这已经意味着我们面临着一个循环任务:任何第步都是通过对进行次评估得到的,即。由于每次评估都存在固有的误差,通常需要对这个过程进行多步的训练,这样网络就能在随着时间推移产生的潜在空间状态漂移方面进行调整。
Koopman算子:在经典的动力系统文献中,对未来状态的数据驱动预测通常是以所谓的"Koopman算子"的形式来表述的,它通常采用矩阵的形式,即使用线性方法。传统的研究主要集中在获得良好的"Koopman算子",以及与基函数结合来覆盖解空间的方法。在上面概述的方法中,网络可以看作是一个非线性的Koopman算子。
为了使这种方法有效,我们需要适当的先前状态历史来唯一确定正确的下一个状态,或者我们的网络必须内部存储它所见过的先前状态历史。
对于前一种情况,预测网络接收多个。对于后一种情况,我们可以借助于循环神经网络(RNNs)子领域中的算法。已经提出了多种架构来编码和存储系统的时间状态,其中最流行的是长短期记忆(LSTM)网络、门控循环单元(GRUs)或最近的基于注意力的Transformer网络。
无论使用哪种变体,这些方法始终使用全连接层,因为潜在空间向量不具有任何空间结构,而通常表示为看似随机的值集合。由于全连接层,预测网络的参数数量迅速增长,因此需要相对较小的潜在空间维度。幸运的是,这与我们在前面概述的主要目标是一致的
27.3 端到端训练
在上述的表述中,我们明确地将编码/解码和时间预测部分进行了分离。然而,在实际应用中,通常更倾向于对涉及特定任务的所有网络进行端到端的训练,因为网络可以根据任务中涉及的其他组件来调整其行为。
对于时间预测,我们可以根据来制定目标,并在时间预测中使用编码器和解码器来计算损失:
理想情况下,这一步骤还会随着时间的推移进行展开,以稳定时间上的演化。由此产生的训练将更加昂贵,因为需要一次性训练更多的权重,并且需要处理更多的中间状态。然而,增加的成本通常会以降低整体推断误差的方式得到回报。
总结一下,深度学习使我们能够从线性子空间转向非线性流形,并为在生成的潜在空间中执行复杂步骤(如时间演化)提供了基础。
27.4 源代码
为了在深度学习领域进行实际实验,我们推荐使用以下两个开源代码库:潜空间模拟代码和学习模型简化代码。
这些代码库实现了端到端的训练,包括编码和预测。它们使用TensorFlow和mantaflow作为深度学习和流体模拟框架。这些代码库旨在关注编码和解码方面的内容。
机器学习中的一个基本问题是充分表示所考虑变量的所有可能状态,即捕捉其完整分布。为了解决这个问题,生成对抗网络(GANs)被证明是深度学习中强大的工具。当数据存在模棱两可的解,并且没有可微分的物理模型可以消除数据的歧义时,GANs尤为重要。在这种情况下,使用监督学习会导致不希望的平均化结果,而采用GANs方法可以避免这种情况发生。

28.1 最大似然估计
为了训练生成对抗网络(GAN),我们需要简要介绍分类问题。对于这些问题,学习目标的形式与{doc}overview-equations中的方程{eq}learn-l2中的回归目标略有不同:我们现在希望最大化学习表示对于给定权重的输入的概率。这导致了以下形式的最大化问题:
经典的最大似然估计(MLE)方法。实际上,通常将其转化为负对数似然之和作为学习目标:
对于这个基本表达式有许多等价的观点,例如,它可以被视为最小化经验分布与学习分布之间的KL散度。它同样表示了对训练数据定义的期望的最大化,即。这又可以等同于分类问题中的经典交叉熵损失,即使用Sigmoid作为激活函数的分类器。在这里的要点是,广泛使用的通过交叉熵进行训练的方法实际上是对输入概率的最大似然估计,如方程{eq}mle-prob所定义。
28.2 对抗训练
MLE是GAN中的一个关键组成部分:在这里,我们有一个生成器(generator),通常类似于一个解码器网络,例如,来自{doc}others-timeseries的自编码器的后半部分。对于常规的GAN,生成器接收一个随机输入向量,并从中生成所需的输出。
然而,我们并不直接训练生成器,而是使用第二个网络作为生成器的损失函数。这个第二个网络称为鉴别器(discriminator),它有一个分类任务:区分生成的样本和“真实”的样本。真实的样本通常以训练数据集的形式提供,下文中将用表示这些样本
对于常规的GAN训练,鉴别器的分类任务通常被表述为:
正如前面所述,这是对于真实样本和生成样本的标准二元交叉熵训练。根据上述公式,鉴别器被训练为对于真实样本产生输出为1,对于生成样本产生输出为0,以最大化损失。
生成器损失的关键在于利用鉴别器,并生成被鉴别器认定为真实的样本:
通常情况下,这种训练是交替进行的,先进行一步的训练,然后进行一步的训练。这样一来,网络保持不变,并为提供梯度,以引导朝着正确的方向生成与真实样本无法区分的样本。由于也是一个神经网络,它在构建时是可微的,能够提供必要的梯度。
28.3 正则化
由于耦合的交替训练,GAN的训练在实践中被认为是棘手的。与单一的非线性优化问题不同,现在我们有了两个相互耦合的问题,需要找到一个脆弱的平衡点。(否则,我们将面临可怕的“模式崩溃”问题:一旦其中一个网络“崩溃”为一个平凡解,耦合训练就会崩溃。)
为了缓解这个问题,正则化通常是实现稳定训练的关键。在最简单的情况下,我们可以为生成器添加一个关于参考数据的正则化项,且系数较小。沿着这个思路,以监督方式预训练生成器可以帮助以一个稳定的状态开始。(然而,通常情况下,鉴别器也需要一定程度的预训练来保持平衡。)
28.4 条件 GAN
对于物理问题来说,传统的生成对抗网络(GAN)从上述随机化的潜空间 生成解并不是特别有用。相反,我们通常会有诸如参数、边界条件或部分解决方案等输入,这些输入应该用于推断输出。这种情况下使用的是条件GAN,也就是说,我们现在有的是 而不是 ,其中 表示输入数据。
条件生成对抗网络(conditional GANs)在超分辨率网络中扮演了重要角色:这些网络的任务是根据稀疏或低分辨率的输入解决方案来计算高分辨率的输出。
28.5 模糊解
GAN的主要优势之一是可以避免模糊数据的不良平均化。例如,考虑超分辨率的情况:一个作为输入的低分辨率观测通常有无限多个可能的高分辨率解,这些解都可以适应低分辨率输入。
如果数据集包含多个这样的情况,并且我们采用监督训练,网络将可靠地学习平均值。这种平均解通常是明显不理想的,与计算它的个别解之一完全不同。这就是多模态问题,即不同模式作为问题的等效解存在的情况。对于流体来说,这可能发生在我们面临分叉的情况下,如{doc}intro-teaser中所讨论的那样。
下面的图片清楚地展示了GAN如何很好地解决这个问题:

28.6 时空超分辨率
当然,GAN的方法并不仅限于空间分辨率。先前的工作已经证明,学习的自我监督概念可以扩展到时空解,例如,在流体模拟的超分辨率背景下 {cite}xie2018tempoGan。
下面的例子将比较不同解的时间导数:

如图所示,经过时空自我监督训练的GAN(从右数第二个)与参考解(最右边)非常接近。在这种情况下,鉴别器接收到随时间变化的参考解(以三元组的形式),从而可以学习判断生成解的时间演化是否与参考解相匹配。
28.7 物理生成模型
最后一个例子是,研究表明GAN也能够准确地捕捉由物理参数参数化的偏微分方程(PDEs)的解流形 {cite}chu2021physgan。在这项工作中,通过改变浮力、涡度含量、边界条件和障碍物几何形状来参数化Navier-Stokes方程的解被神经网络学习到。
这是一个极具挑战性的解决方案流形,需要一种扩展的 "循环 "GAN 方法,推动判别器考虑所有物理参数。该方法可推动判别器将所有物理参数考虑在内。有趣的是,尽管生成器是纯粹根据数据进行训练的,即不需要任何帮助,但它仍能学习生成现实而准确的解。尽管是纯粹根据数据进行训练,即没有可微分物理求解器设置的明确帮助,生成器仍能学习生成真是而准确的解。
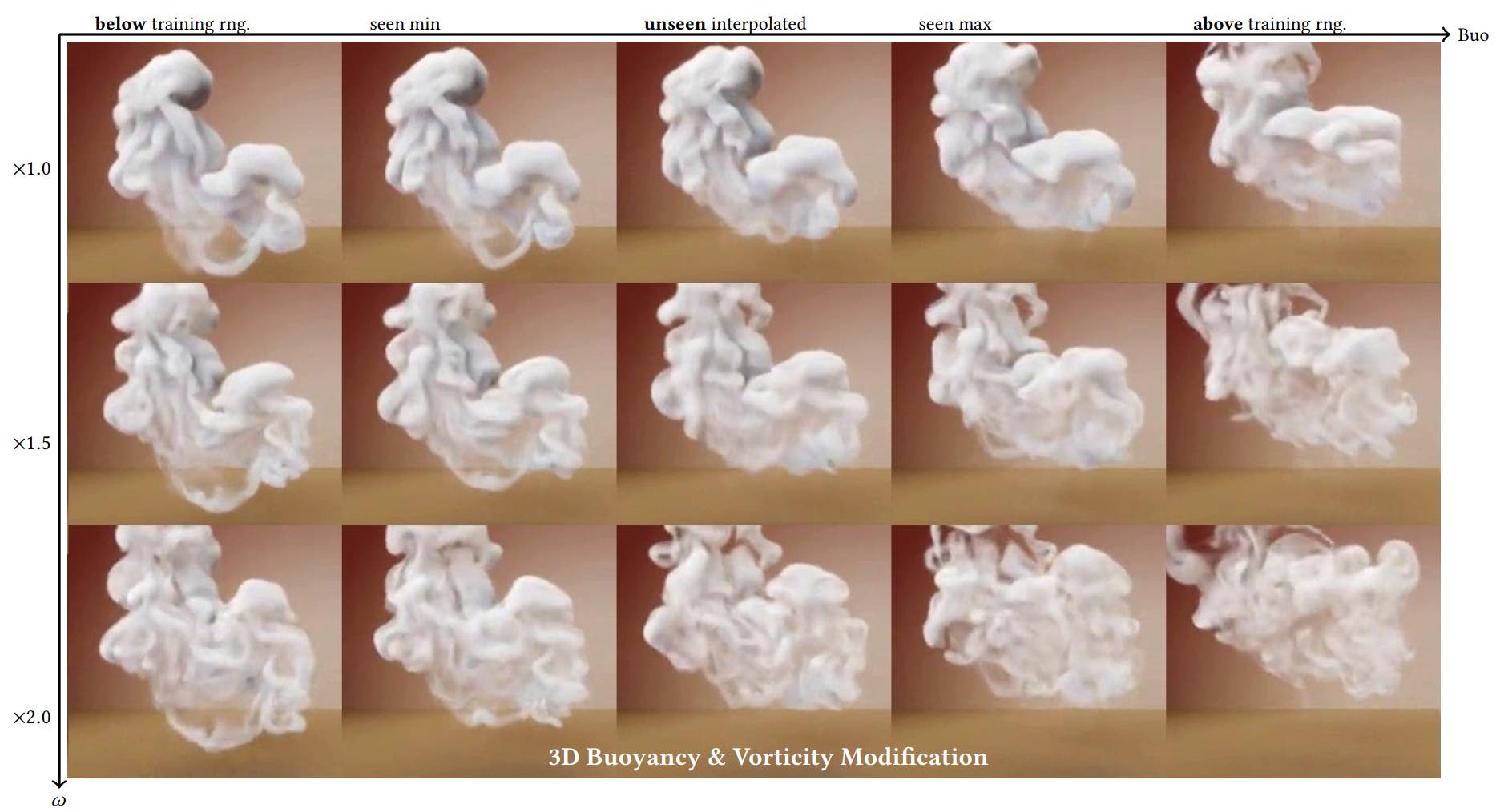
28.8 讨论
GAN是一种强大的学习工具。需要注意的是,鉴别器实际上只是一个学习到的损失函数:一旦生成器完全训练好了,我们在推断阶段可以完全舍弃它。因此,它所需的资源并不是非常关键。
然而,尽管GAN是非常强大的工具,但在我们可以获得合理的PDE模型时,它是否有意义还存在疑问(根据当前的最新技术)。如果我们可以离散化模型方程并将其与可微分的物理(DP)训练结合起来(参见{doc}diffphys),那么这很可能会比使用鉴别器逼近PDE模型获得更好的结果。DP训练可以获得与GAN训练类似的好处:通过离散化的模拟器获得局部梯度,并以此方式防止对样本进行不良的平均化。因此,DP训练与GAN的组合在孤立应用时也不会表现得比它们中的任何一种更好。
话虽如此,当由于没有梯度的黑盒求解器而无法进行DP训练时,GAN仍然可能是一种有吸引力的选择。
28.9 源代码
由于训练设置的复杂性,我们只参考外部开源实现来进行物理生成对抗网络的实际实验。例如,可以在https://github.com/thunil/tempoGAN上找到{xie2018tempoGan}的时空生成对抗网络。
该实现还包括一些用于稳定性的扩展,如L1正则化和生成器-判别器平衡。
对于所有基于计算机的方法,我们需要找到一个适合的“离散”表示方式。对于仅由整数组成的数据,这是很简单的,但对于像房间温度这样不断变化的数量来说,就更具挑战性了。尽管之前的例子侧重于离散化之外的方面(并使用笛卡尔网格作为占位符),但下一章将针对动态变化和自适应离散化具有优势的情境进行学习。
29.1 计算网格类型
一般而言,我们可以区分三种常见的计算网格(或“网格”),用于离散化的方式如下:
-
结构化网格:结构化网格具有样本点的规则排列和隐式定义的连通性。在最简单的情况下,它是一个密集的笛卡尔网格。
-
非结构化网格:另一方面,非结构化网格可以具有任意的连通性和排列方式。这种灵活性通常会增加计算成本。
-
无网格或基于粒子的网格最终与非结构化网格共享样本点的任意排列方式,但通过邻域(即适当的距离度量)隐式定义连通性。
由于结构化网格与图像数据类似,因此在深度学习算法中目前对结构化网格的支持非常好,这通常简化了实现并允许使用稳定、成熟的深度学习组件(尤其是常规卷积层)。然而,对于目标函数在平滑和复杂区域之间呈不均匀混合的情况,其他两种网格类型可能具有优势。

29.2 非结构化网格和图神经网络
在计算科学中,生成更好的网格结构是一个具有挑战性且持续不断的工作。多年来,为了研究机翼周围的流动,提出了许多H型、C型和O型网格,这是一个很好的例子。
非结构化网格在网格划分方面提供了最大的灵活性,但当然需要模拟器的支持。有趣的是,非结构化网格与图神经网络(GNNs)共享许多属性,它将经典的深度学习思想扩展到图结构上的笛卡尔网格。尽管有越来越多的支持,但使用GNNs通常会增加实现的复杂性,而任意的连接性要求在图的节点之间进行“消息传递”方法。这种“消息传递”通常是通过全连接层实现的,而不是卷积层。
因此,在接下来的内容中,我们将重点介绍一种基于粒子的方法(参考文献:Ummerhofer et al., 2019),该方法在空间适应性方面与GNNs具有相同的灵活性。以前,GNNs已被用于实现非常相似的目标(参考文献:Sanchez et al., 2020),然而,下面的这种方法可以实现真正的卷积运算符,从而学习物理关系。
29.3 无网格和基于粒子的方法
在动态情况下,明确组织连接性尤其具有挑战性,例如,对于描述移动材料的拉格朗日表示,其中连接性会随时间迅速过时。在这种情况下,依赖于灵活的、重新计算的连接性的方法是一个不错的选择。操作是根据采样位置(也称为“粒子”或者只是“点”)周围的空间邻域定义的,由于缺乏显式的网格结构,这些方法也被称为“非网格”方法。可以说,不同的非结构化、图形和非网格变体通常可以相互转换,但是上述粗略区分仍然为方法的工作方式提供了一个指示。
接下来,我们将讨论一个以飞溅液体为目标的例子,这是一个特别具有挑战性的情况。对于这些模拟,流体材料的运动非常显著,并且通常分布非常不均匀。
学习的基于粒子的模拟的一般概述类似于在笛卡尔网格上工作的深度学习方法:我们存储在特定位置的数据,如速度,然后重复执行卷积操作,在每个位置创建一个潜空间。每个卷积操作在其支持范围内读取潜空间内容并生成结果,该结果通过适当的非线性函数(如ReLU)进行激活。这个过程同时进行多次,以产生一个潜空间向量,而每个位置的潜空间向量作为下一阶段卷积的输入。在几个层次上扩展潜空间的大小后,再次收缩以产生所需的结果,例如加速度。
29.4 连续卷积
一个通用的、离散的卷积运算符用于计算函数和之间的卷积,其形式为:
其中,表示偏移向量,定义了滤波函数(通常为)的支持。
我们将这个思想应用于粒子和点云,通过在围绕的径向邻域中对一组个位置进行卷积来进行评估。这里,表示卷积应该具有支持的半径。 我们根据Ummerhofer等人(2019)的方法定义了卷积的连续版本:
在这里,映射起着核心作用:它表示从单位球到单位立方体的映射,这使我们可以使用简单的网格来表示卷积核中的未知量。这极大地简化了卷积核的构建和处理,并在下图中进行:

在物理环境中,例如流体动力学的模拟中,我们可以额外引入一个径向加权函数,如下所示表示为,以确保卷积核具有平滑的衰减。这产生了:
这里,表示归一化因子。对于来说,有相当大的灵活性,但在下面我们将使用以下加权函数:
这样可以确保学习到的影响在每个单独的卷积中平滑地降至零。
为了实现精简的架构,可以为每个卷积添加一个小型全连接层,以处理目标粒子本身的内容。这使得可以使用相对较小、且尺寸均匀的卷积核,例如的尺寸(Ummerhofer等人,2019)。
29.5 学习液体动力学
上述的架构可以使用基于粒子的Navier-Stokes求解器的随机参考数据集进行训练。得到的网络模型具有很小且高效的特点,同时提供了很好的准确性。与基于图神经网络的方法相比,连续卷积需要的权重数量更少且评估速度更快。
有趣的是,对于这样一个学习求解器来说,特别具有挑战性的情况是一个应该静止下来的液体容器。如果训练数据没有经过特别设计以包含许多这样的情况,网络在训练时只会接收到相对较少的这类情况。此外,模拟通常需要许多步骤才能达到静止状态(比训练时展开的步骤要多得多)。因此网络并没有明确训练来重现这种行为。
尽管如此, 构建上具有经过训练的神经网络的这种液体模拟的一个有趣的副作用, 提供了一个可微分的求解器。基于预训练网络, 学习求解器然后支持通过梯度下降进行优化, 例如, 针对诸如黏度之类的输入参数。
然而,通过训练神经网络进行液体模拟的一个有趣的副作用是,它提供了一个可微分的求解器。基于预训练的网络,学习到的求解器可以通过梯度下降进行优化,例如针对粘度等输入参数进行优化。

29.6 源代码
对于连续卷积的实际应用,另一个重要步骤是快速收集 的相邻粒子。一个高效的实施示例可以在https://github.com/intel-isl/DeepLagrangianFluids、以及学习液体动力学的训练代码。如上图所示。
尽管我们进行了漫长的讨论并提供了许多示例,但在基于物理的深度学习的背景下,我们只是触及到了问题的表面,对于可能性还只是皮毛而已。
最重要的是,前一章所解释的技术具有巨大的潜力,能够影响未来几十年的所有计算方法。正如代码示例多次证明的那样,其中并没有什么神奇的东西,但深度学习为我们提供了非常强大的工具,用于表示和逼近非线性函数。而且深度学习绝不会使现有的数值方法变得过时,相反,两者是一个理想的组合。
迄今为止,我们完全没有涉及的一个问题是,我们的目标当然是提高人类对世界的理解。在这里,将神经网络视为“黑匣子”的观点显然已经过时。它只是另一种人类可以采用的数值方法,网络预测的物理场与传统模拟的结果一样可解释。然而,进一步改进分析学习网络的工具,并提取网络在解决方案空间中发现的模式和规律的精简表达是很重要的。

30.1 一些具体方向
除了这个长期的展望外,还有许多有趣且即时的步骤。虽然使用Burgers方程和Navier-Stokes求解器的示例显然是非平凡的,但本书的技术可以应用于各种其他潜在的偏微分方程模型。以下只是来自其他领域的几个有前景的
-
化学反应的偏微分方程常常因多种物种的相互作用而表现出复杂的行为。在这里,尤其有趣的方向是训练模型,快速学习预测实验或机器的演变,并调整控制参数以稳定它,即在线的"控制"设置。
-
等离子体模拟与基于液体的涡度公式有很多共同之处,但同时引入了处理材料内部的电磁相互作用的项。同样,等离子体聚变实验和发生器的控制器是一个具有丰富的潜力,可以利用可微分物理的深度学习进行研究。
-
最后,天气和气候是人类非常重要的主题,涉及到液体流动与地球表面上多种现象的高度复杂系统。准确地对所有这些相互作用的系统建模并预测它们的长期行为,展示了深度学习方法与数值模拟相结合的巨大潜力。
30.2 结束语
因此,总的来说,还有很多令人兴奋的研究工作要做--未来几年和几十年肯定不会无聊。

- [AAC+19] Ilge Akkaya, Marcin Andrychowicz, Maciek Chociej, Mateusz Litwin, Bob McGrew, and others. Solving rubik's cube with a robot hand. arXiv: 1910.07113, 2019.
- [CCHT 21]Li-Wei Chen, Berkay A Cakal, Xiangyu Hu, and Nils Thuerey. Numerical investigation of minimum drag profiles in laminar flow using deep learning surrogates. Journal of Fluid Mechanics, 2021. URL: https://ge.in.tum.de/publications/2020-chen-dl-surrogates/.
- [CT 21]Li-Wei Chen and Nils Thuerey. Towards high-accuracy deep learning inference of compressible turbulent flows over aerofoils. In arXiv. 2021. URL: https://ge.in.tum.de/publications/.
- [CTS+21]Mengyu Chu, Nils Thuerey, Hans-Peter Seidel, Christian Theobalt, and Rhaleb Zayer. Learning Meaningful Controls for Fluids. ACM Trans. Graph., 2021. URL: https://people.mpi-inf.mpg.de/~mchu/gvv-den2vel/den2vel.html.
- [Gol 90]H Goldstine. A history of scientific computing. ACM, 1990. ^c6019b
- [HKT 19]Philipp Holl, Vladlen Koltun, and Nils Thuerey. Learning to control pdes with differentiable physics. In International Conference on Learning Representations. 2019. URL: https://ge.in.tum.de/publications/2020-iclr-holl/.
- [HKT 21]Philipp Holl, Vladlen Koltun, and Nils Thuerey. Physical gradients and scale-invariant physics for deep learning. In arXiv: 2109.15048. 2021. URL: https://arxiv.org/abs/2109.15048.
- [KAT+19]Byungsoo Kim, Vinicius C Azevedo, Nils Thuerey, Theodore Kim, Markus Gross, and Barbara Solenthaler. Deep Fluids: A Generative Network for Parameterized Fluid Simulations. Comp. Grap. Forum, 38 (2): 12, 2019. URL: http://www.byungsoo.me/project/deep-fluids/.
- [KB 14]Diederik P Kingma and Jimmy Ba. Adam: a method for stochastic optimization. arXiv: 1412.6980, 2014.
- [KSA+21]Dmitrii Kochkov, Jamie A Smith, Ayya Alieva, Qing Wang, Michael P Brenner, and Stephan Hoyer. Machine learning–accelerated computational fluid dynamics. Proceedings of the National Academy of Sciences, 2021.
- [KUT 20]Georg Kohl, Kiwon Um, and Nils Thuerey. Learning similarity metrics for numerical simulations. International Conference on Machine Learning, 2020. URL: https://ge.in.tum.de/publications/2020-lsim-kohl/.
- [KSH 12]Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems. 2012.
- [LCT 22]Bjoern List, Liwei Chen, and Nils Thuerey. Learned turbulence modelling with differentiable fluid solvers. In arXiv: 2202.06988. 2022. URL: https://ge.in.tum.de/publications/.
- [MLA+19]Rajesh Maingi, Arnold Lumsdaine, Jean Paul Allain, Luis Chacon, SA Gourlay, and others. Summary of the fesac transformative enabling capabilities panel report. Fusion Science and Technology, 75 (3):167–177, 2019. ^5502d2
- [OMalleyBK+16]Peter JJ O’Malley, Ryan Babbush, Ian D Kivlichan, Jonathan Romero, Jarrod R McClean, Rami Barends, Julian Kelly, Pedram Roushan, Andrew Tranter, Nan Ding, and others. Scalable quantum simulation of molecular energies. Physical Review X, 6 (3): 031007, 2016. ^a41ddb
- [Qur 19]Mohammed Al Quraishi. Alphafold at casp 13. Bioinformatics, 35 (22):4862–4865, 2019.
- [RWC+19]Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language models are unsupervised multitask learners. OpenAI blog, 1 (8): 9, 2019.
- [RPK 19]Maziar Raissi, Paris Perdikaris, and George Karniadakis. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019.
- [SGGP+20]Alvaro Sanchez-Gonzalez, Jonathan Godwin, Tobias Pfaff, Rex Ying, Jure Leskovec, and Peter Battaglia. Learning to simulate complex physics with graph networks. In International Conference on Machine Learning, 8459–8468. 2020.
- [SHT 22]Patrick Schnell, Philipp Holl, and Nils Thuerey. Half-inverse gradients for physical deep learning. In ICLR. 2022. URL: https://github.com/tum-pbs/half-inverse-gradients.
- [SML+15]John Schulman, Philipp Moritz, Sergey Levine, Michael Jordan, and Pieter Abbeel. High-dimensional continuous control using generalized advantage estimation. arXiv: 1506.02438, 2015.
- [SWD+17]John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. arXiv: 1707.06347, 2017.
- [SSS+17]David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, and others. Mastering the game of Go without human knowledge. Nature, 2017.
- [Sto 14]Thomas Stocker. Climate change 2013: the physical science basis: Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge university press, 2014. ^49388b
- [SB 18]Richard S Sutton and Andrew G Barto. Reinforcement learning: An introduction. MIT press, 2018.
- [TWPH 20]Nils Thuerey, Konstantin Weissenow, Lukas Prantl, and Xiangyu Hu. Deep learning methods for reynolds-averaged navier–stokes simulations of airfoil flows. AIAA Journal, 58 (1):25–36, 2020. URL: https://ge.in.tum.de/publications/2018-deep-flow-pred/.
- [TSSP 17]Jonathan Tompson, Kristofer Schlachter, Pablo Sprechmann, and Ken Perlin. Accelerating eulerian fluid simulation with convolutional networks. In Proceedings of Machine Learning Research, 3424–3433. 2017.
- [UBH+20]Kiwon Um, Robert Brand, Philipp Holl, Raymond Fei, and Nils Thuerey. Solver-in-the-loop: learning from differentiable physics to interact with iterative pde-solvers. Advances in Neural Information Processing Systems, 2020. URL: https://ge.in.tum.de/publications/2020-um-solver-in-the-loop/.
- [UPTK 19]Benjamin Ummenhofer, Lukas Prantl, Nils Thuerey, and Vladlen Koltun. Lagrangian fluid simulation with continuous convolutions. In International Conference on Learning Representations. 2019. URL: https://ge.in.tum.de/publications/2020-ummenhofer-iclr/.
- [WBT 19]Steffen Wiewel, Moritz Becher, and Nils Thuerey. Latent-space Physics: Towards Learning the Temporal Evolution of Fluid Flow. Comp. Grap. Forum, 38 (2): 12, 2019. URL: https://ge.in.tum.de/publications/latent-space-physics/.
- [WKA+20]Steffen Wiewel, Byungsoo Kim, Vinicius C Azevedo, Barbara Solenthaler, and Nils Thuerey. Latent space subdivision: stable and controllable time predictions for fluid flow. Symposium on Computer Animation, 2020. URL: https://ge.in.tum.de/publications/2020-lssubdiv-wiewel/.
- [XFCT18]You Xie, Erik Franz, Mengyu Chu, and Nils Thuerey. tempoGAN: A Temporally Coherent, Volumetric GAN for Super-resolution Fluid Flow. ACM Trans. Graph., 2018. URL: https://ge.in.tum.de/publications/tempogan/.
数学符号
| Symbol | Meaning |
|---|---|
| 矩阵 | |
| 学习率或步长 | |
| 计算域 的边界 | |
| 要近似的通用函数,通常是未知的。 | |
| 的近似版本 | |
| 计算区域 | |
| 连续/理想物理模型 | |
| 离散物理模型 | |
| 神经网络参数 | |
| 时间维度 | |
| 矢量速度 | |
| 神经网络输入或空间坐标 | |
| 神经网络输出 | |
| 学习目标:基本事实、参考或观察数据 |
重要缩写的摘要
| ABbreviation | Meaning |
|---|---|
| BNN | 贝叶斯神经网络 |
| CNN | 卷积神经网络 |
| DL | 深度学习 |
| GD | 梯度下降 |
| MLP | 多层感知机,一种具有全连接层的神经网络 |
| NN | 神经网络(通用网络,与 CNN 或 MLP 等网络不同) |
| PDE | 偏微分方程 |
| PBDL | 基于物理的深度学习 |
| SGD | 随机梯度下降 |
数学符号
| Symbol | Meaning |
|---|---|
| matrix | |
| learning rate or step size | |
| boundary of computational domain | |
| generic function to be approximated, typically unknown | |
| approximate version of | |
| computational domain | |
| continuous/ideal physical model | |
| discretized physical model, PDE | |
| neural network params | |
| time dimension | |
| vector-valued velocity | |
| neural network input or spatial coordinate | |
| neural network output | |
| learning targets: ground truth, reference or observation data |
重要缩写的摘要
| ABbreviation | Meaning |
|---|---|
| BNN | Bayesian neural network |
| CNN | Convolutional neural network |
| DL | Deep Learning |
| GD | (steepest) Gradient Descent |
| MLP | Multi-Layer Perceptron, a neural network with fully connected layers |
| NN | Neural network (a generic one, in contrast to, e.g., a CNN or MLP) |
| PDE | Partial Differential Equation |
| PBDL | Physics-Based Deep Learning |
| SGD | Stochastic Gradient Descent |