在本笔记本中，我们将通过一个实际例子来比较半反梯度（HIGs）与其他用于训练具有物理损失函数的神经网络的方法。具体而言，我们将比较以下几种方法：

Adam：作为标准的基于梯度下降（GD）的网络优化器，
尺度不变物理学：先前描述的完全反演物理学的算法，
半逆梯度：在局部和联合反演物理学和网络。

22.1 反问题设置

学习任务是找到控制函数来控制耦合振荡器系统的动力学。这是物理学中的一个经典问题，也是一个评估HIGs的好案例，因为它的规模较小。我们使用两个质点，因此对于两个质点的位置和速度，我们只有四个自由度（相对于例如仅具有32个单元格沿x和y的“小”流体模拟，我们将获得 $32 \times 32 \times 2$ 个未知数）。

尽管如此，振荡器是一个高度非平凡的案例：我们的目标是应用控制，使得在选择的时间间隔后再次达到初始状态。我们将使用24步四阶Runge-Kutta方案，因此NN必须学习如何在所有时间步骤中最好地“推动”两个质点，使它们在正确的时间以正确的速度到达所需的位置。

一个由 $N$ 个耦合振子组成的系统可以用以下哈密顿量描述：

$H (x_{i}, p_{i}, t) = i \sum (\frac{x _{i}^{2}}{2} + \frac{p _{i}^{2}}{2} + α \cdot (x_{i} - x_{i + 1})^{4} + u (t) \cdot x_{i} \cdot c_{i})$

它为下面的 RK 4 时间积分提供了基础。

22.2 问题描述

更具体地说，我们考虑一组不同的物理输入（ $x_{i}$ ）。通过使用相应的控制函数（ $u_{i}$ ），我们可以影响我们的物理系统 $P$ 的时间演化并获得一个输出状态（ $y_{i}$ ）：

$y_{i} = P (x_{i}; u_{i})$

如果我们想将给定的初始状态（ $x_{i}$ ）演化为给定的目标状态（ $y_{i}^{*}$ ），我们就会得到一个控制函数（ $u_{i}$ ）的反问题。期望目标状态（ $y_{i}^{*}$ ）与接收到的目标状态（ $y_{i}$ ）之间的质量由损失函数（ $L$ ）来衡量。

$arg min_{u_{i}} L (y_{i}^{*}, P (x_{i}; u_{i}))$

如果我们使用一个神经网络（ $f$ 参数化为 $θ$ ）来学习一组输入/输出对（ $x_{i}, y_{i}^{*}$ ）上的控制函数，我们将上述物理优化任务转化为一个学习问题。

$arg min_{θ} i \sum L (y_{i}^{*}, P (x_{i}; f (x_{i}, y_{i}; θ)))$

在设置物理求解器 $P$ 之前，我们导入必要的库（本例使用TensorFlow），并定义主要的全局变量MODE，它在_Adam_('GD')、尺度不变物理('SIP')和_半反梯度_('HIG')之间切换。


import numpy as np
import tensorflow as tf
import time, os

# main switch for the three methods:
MODE = 'HIG'  # HIG | SIP | GD

22.3 耦合线性振子模拟

对于物理模拟，我们将解决一个耦合线性振子系统带有控制项的微分方程。时间积分使用四阶龙格-库塔方案。

下面，我们首先定义一些全局常量：Nx：振子的数量，Nt：时间演化步数，以及DT：一个时间步长的长度。然后我们定义一个帮助函数来设置一个拉普拉斯模板，名为coupled_oscillators_batch()的函数计算整个小批量值的模拟，最后是solver()函数，它使用给定的控制信号运行所需的时间步数。


Nx = 2
Nt = 24
DT = 0.5

def build_laplace(n,boundary='0'):
    if n==1:
        return np.zeros((1,1),dtype=np.float32)
    d1 = -2 * np.ones((n,),dtype=np.float32)
    d2 = 1 * np.ones((n-1,),dtype=np.float32)
    lap = np.zeros((n,n),dtype=np.float32)
    lap[range(n),range(n)]=d1
    lap[range(1,n),range(n-1)]=d2
    lap[range(n-1),range(1,n)]=d2
    if boundary=='0':
        lap[0,0]=lap[n-1,n-1]=-1

    return lap

@tf.function
def coupled_oscillators_batch( x, control):
    '''
    ODE of type:    x' = f(x)
    :param x_in:    position and velocities, shape: (batch, 2 * number of osc) order second index: x_i , v_i
    :param control: control function, shape: (batch,)
    :return:
    '''
    #print('coupled_oscillators_batch')
    n_osc = x.shape[1]//2

    # natural time evo
    a1 = np.array([[0,1],[-1,0]],dtype=np.float32)
    a2 = np.eye(n_osc,dtype=np.float32)
    A = np.kron(a1,a2)
    x_dot1 = tf.tensordot(x,A,axes = (1,1))

    # interaction term
    interaction_strength = 0.2
    b1 = np.array([[0,0],[1,0]],dtype=np.float32)
    b2 = build_laplace(n_osc)
    B = interaction_strength * np.kron(b1,b2)
    x_dot2 = tf.tensordot(x,B, axes=(1, 1))

    # control term
    control_vector = np.zeros((n_osc,),dtype=np.float32)
    control_vector[-1] = 1.0
    c1 = np.array([0,1],dtype=np.float32)
    c2 = control_vector
    C = np.kron(c1,c2)
    x_dot3 = tf.tensordot(control,C, axes=0)

    #all terms
    x_dot = x_dot1 + x_dot2 +x_dot3
    return x_dot

@tf.function
def runge_kutta_4_batch(x_0, dt, control, ODE_f_batch):

    f_0_0 = ODE_f_batch(x_0, control)
    x_14 = x_0 + 0.5 * dt * f_0_0

    f_12_14 = ODE_f_batch(x_14, control)
    x_12 = x_0 + 0.5 * dt * f_12_14

    f_12_12 = ODE_f_batch(x_12, control)
    x_34 = x_0 + dt * f_12_12

    terms = f_0_0 + 2 * f_12_14 + 2 * f_12_12 + ODE_f_batch(x_34, control)
    x1 = x_0 + dt * terms / 6

    return x1

@tf.function
def solver(x0, control):
    x = x0
    for i in range(Nt):
        x = runge_kutta_4_batch(x, DT, control[:,i], coupled_oscillators_batch)
    return x

22.4 训练设置

神经网络本身非常简单：它由四个密集层组成（中间的每个层有20个神经元），并使用tanh激活函数。


act = tf.keras.activations.tanh
model = tf.keras.models.Sequential([
    tf.keras.layers.InputLayer(input_shape=(2*Nx)),
    tf.keras.layers.Dense(20, activation=act),
    tf.keras.layers.Dense(20, activation=act),
    tf.keras.layers.Dense(20, activation=act),
    tf.keras.layers.Dense(Nt, activation='linear')
    ])

作为损失函数, 我们将使用 $L^{2}$ 损失:


@tf.function
def loss_function(a,b):
    diff = a-b
    loss_batch = tf.reduce_sum(diff**2,axis=1)
    loss = tf.reduce_sum(loss_batch)
    return loss

作为训练的数据集，我们简单地创建了4k个随机位置值，这些位置值是振荡器在模拟开始时的初始状态（X_TRAIN），并且在模拟结束时应该返回到这些初始状态（Y_TRAIN）。由于它们应该返回到初始状态，我们有X_TRAIN=Y_TRAIN。


N = 2**12
X_TRAIN = np.random.rand(N, 2 * Nx).astype(np.float32)
Y_TRAIN = X_TRAIN # the target states are identical

22.5 训练

神经网络训练的优化过程需要设置一些全局参数。下一个单元格初始化了适合三种方法的一些合适值。这些值是根据经验确定的，对于每种方法都能够发挥最佳效果。如果我们尝试为所有方法使用相同的设置，这将不可避免地使其中一些方法的比较不公平。

Adam：这是最广泛使用的神经网络优化器，我们在这里使用它作为GD家族的代表。请注意，截断参数对Adam没有意义。
SIP：指定的优化器是用于网络优化的。物理反演是通过高斯-牛顿完成的，并且对应于精确反演，因为物理优化景观是二次的。对于高斯-牛顿中的雅可比矩阵反演，我们可以指定截断参数。
HIG：要获得HIG算法，必须将优化器设置为SGD。对于雅可比矩阵的半反演，我们可以指定截断参数。最佳批量大小通常比其他两种方法要低，学习率为1通常非常有效。

最大训练时间以秒为单位通过下面的 MAX_TIME 设置。


if MODE=='HIG': # HIG training
  OPTIMIZER = tf.keras.optimizers.SGD
  BATCH_SIZE = 32 # larger batches make HIGs unnecessariy slow...
  LR = 1.0
  TRUNC = 10**-10

elif MODE=='SIP': # SIP training
  OPTIMIZER = tf.keras.optimizers.Adam
  BATCH_SIZE = 256
  LR = 0.001  # for the internal step with Adam
  TRUNC = 0   # not used

else: #  Adam Training (as GD representative)
  MODE = 'GD' 
  OPTIMIZER = tf.keras.optimizers.Adam
  BATCH_SIZE = 256
  LR = 0.001
  TRUNC = 0 # not used

# global parameters for all three methods
MAX_TIME = 100 # [s]
print("Running variant: "+MODE)

输出结果：


Running variant: HIG

下一个函数HIG_pinv()是一个关键函数：它用于构建给定HIGs矩阵的半逆。它计算SVD，取奇异值的平方根，然后重新组装矩阵。


from tensorflow.python.framework import ops
from tensorflow.python.framework import tensor_shape
from tensorflow.python.ops import array_ops
from tensorflow.python.ops import math_ops
from tensorflow.python.util import dispatch
from tensorflow.python.util.tf_export import tf_export
from tensorflow.python.ops.linalg.linalg_impl import _maybe_validate_matrix,svd

# partial inversion of the Jacobian via SVD:
# this function is adopted from tensorflow's SVD function, and published here under its license: Apache-2.0 License , https://github.com/tensorflow/tensorflow/blob/master/LICENSE
@tf_export('linalg.HIG_pinv')
@dispatch.add_dispatch_support
def HIG_pinv(a, rcond=None,beta=0.5, validate_args=False, name=None):

  with ops.name_scope(name or 'pinv'):
    a = ops.convert_to_tensor(a, name='a')

    assertions = _maybe_validate_matrix(a, validate_args)
    if assertions:
      with ops.control_dependencies(assertions):
        a = array_ops.identity(a)

    dtype = a.dtype.as_numpy_dtype

    if rcond is None:

      def get_dim_size(dim):
        dim_val = tensor_shape.dimension_value(a.shape[dim])
        if dim_val is not None:
          return dim_val
        return array_ops.shape(a)[dim]

      num_rows = get_dim_size(-2)
      num_cols = get_dim_size(-1)
      if isinstance(num_rows, int) and isinstance(num_cols, int):
        max_rows_cols = float(max(num_rows, num_cols))
      else:
        max_rows_cols = math_ops.cast(
            math_ops.maximum(num_rows, num_cols), dtype)
      rcond = 10. * max_rows_cols * np.finfo(dtype).eps

    rcond = ops.convert_to_tensor(rcond, dtype=dtype, name='rcond')

    [ singular_values, left_singular_vectors, right_singular_vectors, ] = svd(
        a, full_matrices=False, compute_uv=True)

    cutoff = rcond * math_ops.reduce_max(singular_values, axis=-1)
    singular_values = array_ops.where_v2(
        singular_values > array_ops.expand_dims_v2(cutoff, -1), singular_values**beta,
        np.array(np.inf, dtype))

    a_pinv = math_ops.matmul(
        right_singular_vectors / array_ops.expand_dims_v2(singular_values, -2),
        left_singular_vectors,
        adjoint_b=True)

    if a.shape is not None and a.shape.rank is not None:
      a_pinv.set_shape(a.shape[:-2].concatenate([a.shape[-1], a.shape[-2]]))

    return a_pinv

现在我们已经准备好运行训练了。下一个单元格定义了一个Python类来组织神经网络优化。它接收物理求解器、网络模型、损失函数和数据集，并在给定的时间限制MAX_TIME内运行尽可能多的周期。

根据选择的优化方法，小批量更新有所不同：

Adam：计算损失梯度，然后应用Adam更新。
PG：计算损失梯度和物理雅可比矩阵，逐个数据点地求逆，通过代理损失和Adam计算网络更新。
HIG：计算损失梯度和网络-物理雅可比矩阵，然后联合计算半求逆，并使用得到的步长更新网络参数。

优化器类的mini_batch_update()方法实现了这三种变体。


class Optimization():
    def __init__(self,model,solver,loss_function,x_train,y_train):
        self.model = model
        self.solver = solver
        self.loss_function = loss_function
        self.x_train = x_train
        self.y_train = y_train
        self.y_dim = y_train.shape[1]
        self.weight_shapes = [weight_tensor.shape for weight_tensor in self.model.trainable_weights]

    def set_params(self,batch_size,learning_rate,optimizer,max_time,mode,trunc):
        self.number_of_batches = N // batch_size
        self.max_time = max_time
        self.batch_size = batch_size
        self.learning_rate = learning_rate
        self.optimizer = optimizer(learning_rate)
        self.mode = mode
        self.trunc = trunc


    def computation(self,x_batch, y_batch):
        control_batch = self.model(y_batch)
        y_prediction_batch = self.solver(x_batch,control_batch)
        loss = self.loss_function(y_batch,y_prediction_batch)
        return loss


    @tf.function
    def gd_get_derivatives(self,x_batch, y_batch):

        with tf.GradientTape(persistent=True) as tape:
            tape.watch(self.model.trainable_variables)
            loss = self.computation(x_batch,y_batch)
            loss_per_dp = loss / self.batch_size
        grad = tape.gradient(loss_per_dp, self.model.trainable_variables)
        return grad


    @tf.function
    def pg_get_physics_derivatives(self,x_batch, y_batch): # physics gradient for SIP

        with tf.GradientTape(persistent=True) as tape:
            control_batch = self.model(y_batch)
            tape.watch(control_batch)
            y_prediction_batch = self.solver(x_batch,control_batch)
            loss = self.loss_function(y_batch,y_prediction_batch)
            loss_per_dp = loss / self.batch_size

        jacy = tape.batch_jacobian(y_prediction_batch,control_batch)
        grad = tape.gradient(loss_per_dp, y_prediction_batch)
        return jacy,grad,control_batch

    @tf.function
    def pg_get_network_derivatives(self,x_batch, y_batch,new_control_batch): #physical grads

        with tf.GradientTape(persistent=True) as tape:
            tape.watch(self.model.trainable_variables)
            control_batch = self.model(y_batch)
            loss = self.loss_function(new_control_batch,control_batch)
            #y_prediction_batch = self.solver(x_batch,control_batch)
            #loss = self.loss_function(y_batch,y_prediction_batch)
            loss_per_dp = loss / self.batch_size

        network_grad = tape.gradient(loss_per_dp, self.model.trainable_variables)
        return network_grad

    @tf.function
    def hig_get_derivatives(self,x_batch,y_batch):

        with tf.GradientTape(persistent=True) as tape:
            tape.watch(self.model.trainable_variables)
            control_batch = self.model(y_batch)
            y_prediction_batch = self.solver(x_batch,control_batch)
            loss = self.loss_function(y_batch,y_prediction_batch)
            loss_per_dp = loss / self.batch_size

        jacy = tape.jacobian(y_prediction_batch, self.model.trainable_variables, experimental_use_pfor=True)
        loss_grad = tape.gradient(loss_per_dp, y_prediction_batch)
        return jacy, loss_grad


    def mini_batch_update(self,x_batch, y_batch):
        if self.mode=="GD":
            grad = self.gd_get_derivatives(x_batch, y_batch)
            self.optimizer.apply_gradients(zip(grad, self.model.trainable_weights))

        elif self.mode=="SIP":
            jacy,grad,control_batch = self.pg_get_physics_derivatives(x_batch, y_batch)
            grad_e = tf.expand_dims(grad,-1)
            pinv = tf.linalg.pinv(jacy,rcond=10**-5)
            delta_control_label_batch = (pinv@grad_e)[:,:,0]
            new_control_batch = control_batch - delta_control_label_batch
            network_grad = self.pg_get_network_derivatives(x_batch, y_batch,new_control_batch)
            self.optimizer.apply_gradients(zip(network_grad, self.model.trainable_weights))

        elif self.mode =='HIG':
            jacy, grad = self.hig_get_derivatives(x_batch, y_batch)
            flat_jacy_list = [tf.reshape(jac, (self.batch_size * self.y_dim, -1)) for jac in jacy]
            flat_jacy = tf.concat(flat_jacy_list, axis=1)
            flat_grad = tf.reshape(grad, (-1,))
            inv = HIG_pinv(flat_jacy, rcond=self.trunc)
            processed_derivatives = tf.tensordot(inv, flat_grad, axes=(1, 0))
            #processed_derivatives = self.linear_solve(flat_jacy, flat_grad)
            update_list = []
            l1 = 0
            for k, shape in enumerate(self.weight_shapes):
                l2 = l1 + np.prod(shape)
                upd = processed_derivatives[l1:l2]
                upd = np.reshape(upd, shape)
                update_list.append(upd)
                l1 = l2
            self.optimizer.apply_gradients(zip(update_list, self.model.trainable_weights))


    def epoch_update(self):
        for batch_index in range(self.number_of_batches):
            position = batch_index * self.batch_size
            x_batch = self.x_train[position:position + self.batch_size]
            y_batch = self.y_train[position:position + self.batch_size]
            self.mini_batch_update(x_batch, y_batch)

    def eval(self,epoch,wc_time,ep_dur):
        train_loss = self.computation(self.x_train,self.y_train)
        train_loss_per_dp = train_loss / N
        if epoch<5 or epoch%20==0: print('Epoch: ', epoch,', wall clock time: ',wc_time,', loss: ', float(train_loss_per_dp) )
        #print('TrainLoss:', train_loss_per_dp)
        #print('Epoch: ', epoch,' WallClockTime: ',wc_time,' EpochDuration: ',ep_dur )
        return train_loss_per_dp

    def start_training(self):
        init_loss = self.eval(0,0,0)
        init_time = time.time()
        time_list = [init_time]
        loss_list = [init_loss]

        epoch=0
        wc_time = 0

        while wc_time<self.max_time:
            
            duration = time.time()
            self.epoch_update()
            duration = time.time()-duration

            epoch += 1
            wc_time += duration

            loss = self.eval(epoch,wc_time,duration)
            time_list.append(duration)
            loss_list.append(loss)

        time_list = np.array(time_list)
        loss_list = np.array(loss_list)
        time_list[0] = 0
        return time_list, loss_list

剩下的就是使用选择的全局参数开始训练，并将结果收集在time_list和loss_list中。


opt = Optimization(model, solver, loss_function, X_TRAIN, Y_TRAIN)
opt.set_params(BATCH_SIZE, LR, OPTIMIZER, MAX_TIME, MODE, TRUNC)
time_list, loss_list = opt.start_training()


Epoch:  0 , wall clock time:  0 , loss:  1.4401766061782837
Epoch:  1 , wall clock time:  28.06755018234253 , loss:  5.44398972124327e-05
Epoch:  2 , wall clock time:  31.38792371749878 , loss:  1.064436037268024e-05
Epoch:  3 , wall clock time:  34.690271854400635 , loss:  3.163525434501935e-06
Epoch:  4 , wall clock time:  37.9914448261261 , loss:  1.1857609933940694e-06

22.6 评估

现在我们可以评估培训过程随时间的收敛情况。以下图表显示了损失随时间（以秒为单位）的演变。


import matplotlib.pyplot as plt

plt.plot(np.cumsum(time_list),loss_list)
plt.yscale('log')
plt.xlabel('Wall clock time [s]'); plt.ylabel('Loss')
plt.title('Linear chain - '+MODE+' with '+str(OPTIMIZER.__name__))
plt.show()

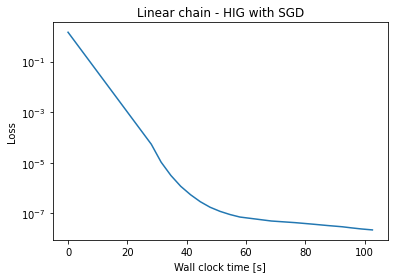
对于这三种方法，你会看到一个很大的线性步骤，就在开始时。由于我们正在公平地测量整个运行时间，因此这个第一步包括了所有TensorFlow初始化步骤，对于HIG和SIP而言，这些步骤显著更为复杂。Adam在初始化方面要快得多，并且每个训练迭代也同样更快。

这三种方法本身都能降低损失。更有趣的是看它们如何比较。为此，下一个单元格会存储训练演变，并且需要使用这三种方法中的每一种运行一次来生成最终的比较图。


path = '/home/'
namet = 'time'
namel = 'loss'
np.savetxt(path+MODE+namet+'.txt',time_list)
np.savetxt(path+MODE+namel+'.txt',loss_list)

在使用每种方法进行运行后，我们可以将它们并列显示：


from os.path import exists

# if previous runs are available, compare all 3
if exists(path+'HIG'+namet+'.txt') and exists(path+'HIG'+namel+'.txt') and exists(path+'SIP'+namet+'.txt') and exists(path+'SIP'+namel+'.txt') and exists(path+'GD'+namet+'.txt') and exists(path+'GD'+namel+'.txt'):
  lt_hig = np.loadtxt(path+'HIG'+namet+'.txt')
  ll_hig = np.loadtxt(path+'HIG'+namel+'.txt')

  lt_sip = np.loadtxt(path+'SIP'+namet+'.txt')
  ll_sip = np.loadtxt(path+'SIP'+namel+'.txt')

  lt_gd = np.loadtxt(path+'GD'+namet+'.txt')
  ll_gd = np.loadtxt(path+'GD'+namel+'.txt')

  plt.plot(np.cumsum(lt_gd),ll_gd,   label="GD")
  plt.plot(np.cumsum(lt_sip),ll_sip, label="SIP")
  plt.plot(np.cumsum(lt_hig),ll_hig,   label="HIG")
  plt.yscale('log')
  plt.xlabel('Wall clock time [s]'); plt.ylabel('Training loss'); plt.legend()
  plt.title('Linear chain comparison ')
  plt.show()
else:
  print("Run this notebook three times with MODE='HIG|SIP|GD' to produce the final graph")

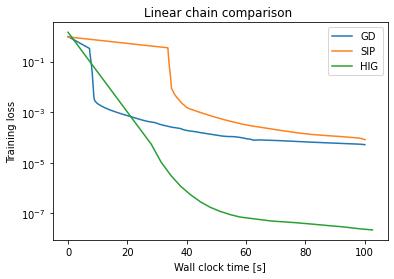
这个图表清晰地显示了收敛方面的显著差异：Adam（蓝色“GD”曲线）执行了大量的更新，但其对黑塞矩阵的粗略近似不足以收敛到高精度，它停滞在高损失水平上。

在这种情况下，SIP更新并没有超越Adam。这是由于相对简单的物理（线性振荡器）以及SIP更高的运行时成本所致。如果您在这个例子中运行得更久一些，SIP实际上会超过Adam，但开始受到完全反演的数值问题的影响。

HIGs的表现比另外两种方法要好得多：尽管每次迭代相对较慢，但半反演产生了非常好的更新，使得训练能够非常快速地收敛到非常低的损失值。HIGs达到的精度比其他两种方法高四个数量级左右。

22.7 下一步

这个笔记本有许多有趣的方向可以进行进一步的测试和修改：

最重要的是，到目前为止，我们实际上只看了训练表现！这使得笔记本保持了相对较短的长度，但这显然是不好的做法。虽然我们声称HIGs同样适用于_真实_测试数据，但这是使用这个笔记本的一个很好的下一步：分配适当的测试样本，并在测试数据上重新运行三种方法的评估。
此外，您可以改变物理行为：使用更多的振荡器来延长或缩短时间跨度，甚至包括非线性力（如HIG论文中所用）。请注意：对于后者，SIP版本将需要一个新的逆求解器。