前面的部分对不同优化方法的优缺点进行了许多评论。接下来，我们将通过一个实际例子展示这些特性实际上产生了多大的差异。

run in colab

18.1 问题描述

我们将考虑一个非常简单的设置，以清楚地说明发生了什么：我们有一个二维输入空间$\mathbf{x}$，一个同样具有两个维度的模拟“物理模型”$\mathbf{y}$，以及一个标量损失$L$，即$\mathbf{x}\in {\mathbb{R}}^2$，$\mathbf{y}:{\mathbb{R}}^2\to {\mathbb{R}}^2$，以及$L:{\mathbb{R}}^2\to \mathbb{R}$。向量$\mathbf{x}$的分量用$x_i$表示，并且为了与Python数组保持同步，索引从0开始。

具体而言，我们将使用以下$\mathbf{y}$和$L$：

\quad \mathbf{y}(\mathbf{x}) = \mathbf{y}(x_0, x_1) = \begin{bmatrix} x_0 \ x_1^2 \end{bmatrix}

即 $\mathbf{y}$ 仅对其输入的第二个分量进行平方，$L(\mathbf{y})=|\mathbf{y}{|}^2=y_0^2+y_1^2$ 表示一个简单的平方 $L^2$ 损失。作为一些示例优化的起点，我们将使用 \mathbf{x} = \begin{bmatrix} 3 \ 3 \end{bmatrix} 作为解决以下简单最小化问题的初始猜测：${\text{arg min}}_{\mathbf{x}}L(\mathbf{x})$。

对于我们人类来说，$[00{]}^T$ 是正确的答案，但让我们看看前面讨论的不同优化算法如何快速找到该解。

18.2 三个空间

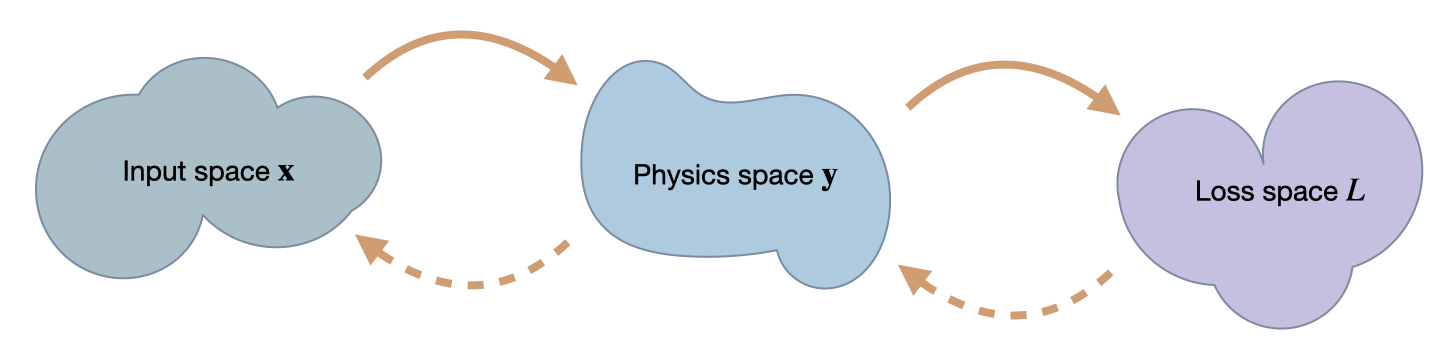
为了理解以下示例，重要的是要记住我们在这里处理的是三个“空间”之间的映射：$\mathbf{x}$、$\mathbf{y}$和$L$。常规前向传递通过$\mathbf{y}$将$\mathbf{x}$映射到$L$，而对于优化，我们需要将$L$中的值和变化与$\mathbf{x}$中的位置相关联。在这样做的同时，有趣的是看看在寻找$\mathbf{x}$的正确位置时，它是如何影响到在$\mathbf{y}$中形成的位置。

18.3 实现

在这个例子中，我们将使用JAX框架，它是一个有效地处理可微函数的良好选择。JAX还有一个很好的numpy封装，实现了大部分numpy的函数。下面我们将使用这个封装作为np，而将原始的numpy作为onp。

import jax
import jax.numpy as np
import numpy as onp

我们将首先定义$\mathbf{y}$和$L$函数，以及一个调用L和y的复合函数fun。对于许多JAX操作，拥有一个单一的本地Python函数是必要的。

# "physics" function y
def physics_y(x):
    return np.array( [x[0], x[1]*x[1]] )

# simple L2 loss
def loss_y(y):
    #return y[0]*y[0] + y[1]*y[1] # "manual version"
    return np.sum( np.square(y) )

# composite function with L & y , evaluating the loss for x
def loss_x(x):
    return loss_y(physics_y(x))


x = np.asarray([3,3], dtype=np.float32)
print("Starting point x = "+format(x) +"\n")

print("Some test calls of the functions we defined so far, from top to bottom, y, manual L(y), L(y):") 
physics_y(x) , loss_y( physics_y(x) ), loss_x(x) 

Starting point x = [3. 3.]
Some test calls of the functions we defined so far, from top to bottom, y, manual L(y), L(y):

现在我们可以通过jax.grad来评估我们函数的导数。例如，jax.grad(loss_y)(physics_y(x))评估了雅可比矩阵$\partial L/\partial \mathbf{y}$。下面的代码单元格评估了这个雅可比矩阵及其几个变体，并对$\mathbf{y}$的逆雅可比矩阵进行了一次合理性检查。

# this works:
print("Jacobian L(y): " + format(jax.grad(loss_y)(physics_y(x))) +"\n")

# the following would give an error as y (and hence physics_y) is not scalar
#jax.grad(physics_y)(x) 

# computing the jacobian of y is a valid operation:
J = jax.jacobian(physics_y)(x)
print( "Jacobian y(x): \n" + format(J) ) 

# the code below also gives error, JAX grad needs a single function object
#jax.grad( loss_y(physics_y) )(x) 

print( "\nSanity check with inverse Jacobian of y, this should give x again: " + format(np.linalg.solve(J, np.matmul(J,x) )) +"\n")

# instead use composite 'fun' from above
print("Gradient for full L(x): " + format( jax.grad(loss_x)(x) )  +"\n")

Jacobian L(y): [ 6. 18.]

Jacobian y(x): 
[[1. 0.]
 [0. 6.]]

Sanity check with inverse Jacobian of y, this should give x again: [3. 3.]

Gradient for full L(x): [  6. 108.]

最后一行值得仔细观察：在这里，我们打印初始位置的梯度$\partial L/\partial \mathbf{x}$。虽然我们知道我们应该沿对角线朝向原点移动（零向量是最小化器），但是这个梯度并不是非常对角线 - 它在$x_1$方向上有一个强烈的主导分量，其值为108。

让我们看看不同的方法如何应对这种情况。我们将比较以下三种方法：

• 一阶方法梯度下降（即常规的、非随机的、“最陡峭的梯度下降”）
• 牛顿法作为二阶方法的代表，
• 逆模拟器中的标度不变更新。

18.4 梯度下降

对于梯度下降法，在我们的设置中，基于简单梯度的更新方程（见公式{eq}GD-update）给出了如下关于 $\mathbf{x}$ 的更新步骤： $$\begin{array}{rl}\Delta {\mathbf{x}}_{\text{GD}}& =-\eta (J_L{J}_{\mathbf{y}}{)}^T\\ & =-\eta (\frac{\partial L}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{x}}{)}^T\end{array}$$ 其中 $\eta$ 表示步长参数。

让我们从$x=[3,3]$开始使用梯度下降进行优化，并使用$\eta =0.01$更新我们的解十次：

x = np.asarray([3.,3.])
eta = 0.01
historyGD = [x]; updatesGD = []

for i in range(10):
    G = jax.grad(loss_x)(x)
    x += -eta * G
    historyGD.append(x); updatesGD.append(G)
    print( "GD iter %d: "%i + format(x) )

GD iter 0: [2.94      1.9200001]
GD iter 1: [2.8812    1.6368846]
GD iter 2: [2.823576  1.4614503]
GD iter 3: [2.7671044 1.3365935]
GD iter 4: [2.7117622 1.2410815]
GD iter 5: [2.657527  1.1646168]
GD iter 6: [2.6043763 1.1014326]
GD iter 7: [2.5522888 1.0479842]
GD iter 8: [2.501243  1.0019454]
GD iter 9: [2.4512184  0.96171147]

在这里，我们已经打印出了$\mathbf{x}$中的结果位置，并且它们似乎在下降，即向正确的方向移动。最后一个点$[2.4510.962]$距离原点还有2.63的相当距离。

让我们来看一下迭代过程中的进展（演化已存储在上面的history列表中）。蓝色点表示GD迭代中$\mathbf{x}$中的位置，目标在原点处用细黑十字表示。

import matplotlib.pyplot as plt
axes = plt.figure(figsize=(4, 4), dpi=100).gca()
historyGD = onp.asarray(historyGD)
updatesGD = onp.asarray(updatesGD) # for later
axes.scatter(historyGD[:,0], historyGD[:,1], lw=0.5, color='#1F77B4', label='GD')
axes.scatter([0], [0], lw=0.25, color='black', marker='x') # target at 0,0
axes.set_xlabel('x0'); axes.set_ylabel('x1'); axes.legend()

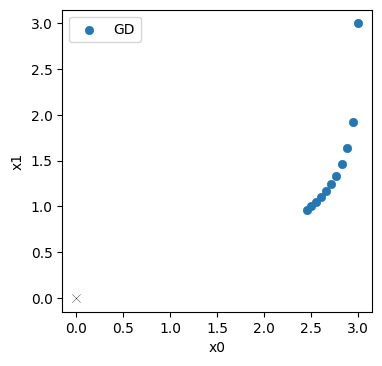
毫不意外的是：初始步骤大部分沿着$x_1$向下移动（在右上角），之后的更新向原点弯曲。但它们并没有走得很远。到达左下角的解仍然相当遥远。

18.5 牛顿法

对于牛顿法， 更新步骤给出 $$\begin{array}{rl}\Delta {\mathbf{x}}_{\text{QN}}& =-\eta {\left(\frac{{\partial }^{2}L}{\partial {\mathbf{x}}^2}\right)}^{-1}\frac{\partial L}{\partial \mathbf{x}}\\ & =-\eta H_L^{-1}(J_L{J}_{\mathbf{y}}{)}^T\end{array}$$ 因此，除了与GD相同的梯度外，我们现在需要评估和求Hessian矩阵$\frac{{\partial }^{2}L}{\partial {\mathbf{x}}^2}$的逆。

在JAX中，这非常简单：我们可以调用jax.jacobian两次，然后使用JAX版本的linalg.inv来反转得到的矩阵。

对于使用牛顿法的优化，我们将使用更大的步长$\eta =1/3$。对于这个例子和下一个例子，我们选择了步长，使得第一次更新步骤的大小大致与GD的大小相同。通过这种方式，我们可以相对于彼此比较所有三种方法的轨迹。请注意，这绝不意味着这里的方法的稳定性或上限的比较。稳定性和$\eta$的上限是分开的主题。这里我们专注于收敛性质。

在下一个单元格中，我们从相同的初始猜测开始应用十次Newton更新：

x = np.asarray([3.,3.])
eta = 1./3.
historyNt = [x]; updatesNt = []

Gx = jax.grad(loss_x)
Hx = jax.jacobian(jax.jacobian(loss_x))
for i in range(10):
    g = Gx(x)
    h = Hx(x)
    hinv = np.linalg.inv(h)
    
    x += -eta * np.matmul( hinv , g )
    historyNt.append(x); updatesNt.append( np.matmul( hinv , g) )
    print( "Newton iter %d: "%i + format(x) )

Newton iter 0: [2.        2.6666667]
Newton iter 1: [1.3333333 2.3703704]
Newton iter 2: [0.88888884 2.1069958 ]
Newton iter 3: [0.59259254 1.8728852 ]
Newton iter 4: [0.39506167 1.6647868 ]
Newton iter 5: [0.26337445 1.4798105 ]
Newton iter 6: [0.17558296 1.315387  ]
Newton iter 7: [0.1170553 1.1692328]
Newton iter 8: [0.07803687 1.0393181 ]
Newton iter 9: [0.05202458 0.92383826]

最后一行已经表明：牛顿法的效果要好得多。最后一个点$[0.0520.924]$到原点的距离只有0.925（相比于梯度下降法的2.63）。

下面，我们将牛顿法的轨迹以橙色绘制在梯度下降法的蓝色版本旁边。

axes = plt.figure(figsize=(4, 4), dpi=100).gca()
historyNt = onp.asarray(historyNt)
updatesNt = onp.asarray(updatesNt) 
axes.scatter(historyGD[:,0], historyGD[:,1], lw=0.5, color='#1F77B4', label='GD')
axes.scatter(historyNt[:,0], historyNt[:,1], lw=0.5, color='#FF7F0E', label='Newton')
axes.scatter([0], [0], lw=0.25, color='black', marker='x') # target at 0,0
axes.set_xlabel('x0'); axes.set_ylabel('x1'); axes.legend()

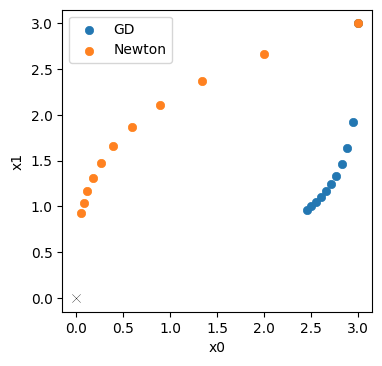
并不完全令人惊讶：对于这个简单的例子，我们可以可靠地评估Hessian矩阵，并且牛顿法从二阶信息中获益。它的轨迹更加沿对角线（这将是理想的、通往解的最短路径），并且不像梯度下降法那样减速明显。

18.6 逆模拟器

现在我们还使用了$\mathbf{y}$的解析逆来进行优化。它代表了我们之前章节中的逆模拟器${\mathcal{P}}^{-1}$：${\mathbf{y}}^{-1}(\mathbf{x})=[x_0{x}_1^{1/2}{]}^T$，用于计算下面所示的尺度不变更新（记为PG）。稍微预告一下下一节，我们将使用牛顿步骤来更新$L$，并将其与逆物理函数结合起来得到整体更新。这给出了一个更新步骤： $$\begin{array}{rl}\Delta {\mathbf{x}}_{\text{PG}}& ={\mathbf{y}}^{-1}\left(\mathbf{y}(\mathbf{x})-\eta {\left(\frac{{\partial }^{2}L}{\partial {\mathbf{y}}^2}\right)}^{-1}\frac{\partial L}{\partial \mathbf{y}}\right)-\mathbf{x}\end{array}$$

下面，我们定义了我们的逆函数physics_y_inv_analytic，然后使用PG更新方法对其进行了十步的优化评估：

x = np.asarray([3.,3.])
eta = 0.3
historyPG = [x]; historyPGy = []; updatesPG = []

def physics_y_inv(y):
    return np.array( [y[0], np.power(y[1],0.5)] )

Gy = jax.grad(loss_y)
Hy = jax.jacobian(jax.jacobian(loss_y))
for i in range(10):
    
    # Newton step for L(y)
    zForw = physics_y(x)
    g = Gy(zForw)
    h = Hy(zForw)
    hinv = np.linalg.inv(h)
    
    # step in y space
    zBack = zForw -eta * np.matmul( hinv , g)
    historyPGy.append(zBack)

    # "inverse physics" step via y-inverse
    x = physics_y_inv(zBack)
    historyPG.append(x)
    updatesPG.append( historyPG[-2] - historyPG[-1] )
    print( "PG iter %d: "%i + format(x) )

PG iter 0: [2.1       2.5099802]
PG iter 1: [1.4699999 2.1000001]
PG iter 2: [1.0289999 1.7569861]
PG iter 3: [0.72029996 1.47      ]
PG iter 4: [0.50421   1.2298902]
PG iter 5: [0.352947 1.029   ]
PG iter 6: [0.24706289 0.86092323]
PG iter 7: [0.17294402 0.7203    ]
PG iter 8: [0.12106082 0.60264623]
PG iter 9: [0.08474258 0.50421   ]

现在我们得到了$[0.0840.504]$作为最终位置，仅有0.51的距离！这显然比牛顿法和梯度下降法都要好。

让我们直接可视化一下与牛顿法（橙色）和梯度下降法（蓝色）相比，PGs（红色）的效果如何。

historyPG = onp.asarray(historyPG)
updatesPG = onp.asarray(updatesPG) 

axes = plt.figure(figsize=(4, 4), dpi=100).gca()
axes.scatter(historyGD[:,0], historyGD[:,1], lw=0.5, color='#1F77B4', label='GD')
axes.scatter(historyNt[:,0], historyNt[:,1], lw=0.5, color='#FF7F0E', label='Newton')
axes.scatter(historyPG[:,0], historyPG[:,1], lw=0.5, color='#D62728', label='PG')
axes.scatter([0], [0], lw=0.25, color='black', marker='x') # target at 0,0
axes.set_xlabel('x0'); axes.set_ylabel('x1'); axes.legend()

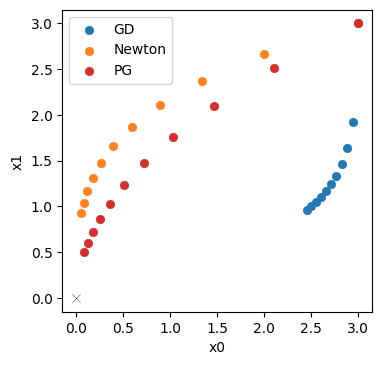
这说明反向模拟器变种红色的PG，甚至比橙色的牛顿法更好。它产生了一条与理想“对角线”轨迹更为一致的轨迹，并且其最终状态更接近原点。这里的一个关键因素是$\mathbf{y}$的反函数，它提供了比牛顿法的二阶近似更高阶的项。这改善了优化的尺度不变性。尽管问题很简单，牛顿法在找到正确的搜索方向方面存在问题。另一方面，反向模拟器更新利用了更高阶的信息，为优化提供了改进的方向。

这种差异也体现在每种方法的第一次更新步骤中：下面我们测量它与对角线的对齐程度。

def mag(x):
    return np.sqrt(np.sum(np.square(x)))

def one_len(x):
    return np.dot( x/mag(x), np.array([1,1])) 

print("Diagonal lengths (larger is better): GD %f, Nt %f, PG %f " % 
      (one_len(updatesGD[0]) , one_len(updatesNt[0]) , one_len(updatesPG[0])) )

Diagonal lengths (larger is better): GD 1.053930, Nt 1.264911, PG 1.356443 

PG 的最大值 1.356 证实了我们上面所看到的：PG 梯度是最接近从起点到原点的对角线方向的梯度。

18.7 y 空间

为了理解这些方法的行为和差异，重要的是要记住，我们不是在处理将$\mathbf{x}$映射到$L$的黑盒子，而是在处理中间的空间。在我们的情况下，我们只有一个$\mathbf{y}$空间，但对于深度学习设置，我们可能有许多潜在空间，我们对其具有一定控制权。我们很快就会回到神经网络，但现在让我们专注于$\mathbf{y}$。

首先要注意的是，对于PG，我们显式地从$L$映射到$\mathbf{y}$，然后继续映射到$\mathbf{x}$。因此，我们已经在$\mathbf{y}$空间中获得了轨迹，并且不巧的是，我们已经将其存储在上面的historyPGy列表中。

让我们直接看看逆模拟器在$\mathbf{y}$空间中做了什么：

historyPGy = onp.asarray(historyPGy)

axes = plt.figure(figsize=(4, 4), dpi=100).gca()
axes.set_title('y space')
axes.scatter(historyPGy[:,0], historyPGy[:,1], lw=0.5, color='#D62728', marker='*', label='PG')
axes.scatter([0], [0], lw=0.25, color='black', marker='*') 
axes.set_xlabel('z0'); axes.set_ylabel('z1'); axes.legend()

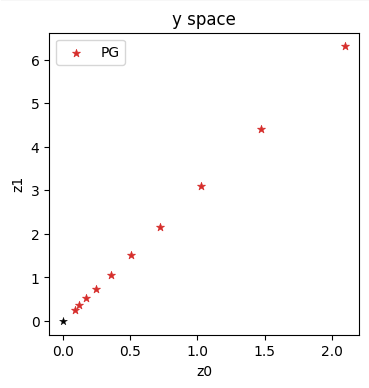
在这个变种中，我们在$\mathbf{y}$空间中采取明确的步骤，这些步骤沿着一条直对角线向原点前进（这也是$\mathbf{y}$空间中的解）。

有趣的是，无论是梯度下降法（GD）还是牛顿法都无法提供关于中间空间（如$\mathbf{y}$空间）进展的信息。

对于梯度下降法，我们正在连接雅可比矩阵，因此我们在局部应该沿着降低损失的方向移动。然而，$\mathbf{y}$的位置受到$\mathbf{x}$的影响，因此在我们确定在$\mathbf{y}$空间的具体点之前，我们不知道最终会到达哪里（对于神经网络来说，一般情况下，在进行梯度下降更新后，我们不知道在哪些潜在空间点上结束，直到我们实际计算出所有更新的权重）。

更具体地说，对于梯度下降法，我们有一个更新$-\eta \frac{\partial L}{\partial \mathbf{x}}$，这意味着我们在$\mathbf{y}$空间中到达$\mathbf{y}(\mathbf{x}-\eta \frac{\partial L}{\partial \mathbf{x}})$。使用$h=\eta \frac{\partial L}{\partial \mathbf{x}}$进行泰勒展开得到： $$\mathbf{y}(\mathbf{x}-h)=\mathbf{y}(\mathbf{x})-h\frac{\partial \mathbf{y}}{\partial \mathbf{x}}+\mathcal{O}(h^2)=\mathbf{y}(x)-\eta \frac{\partial L}{\partial \mathbf{y}}(\frac{\partial \mathbf{y}}{\partial x}{)}^2+\mathcal{O}(h^2)$$

而$\frac{\partial L}{\partial \mathbf{y}}(\frac{\partial \mathbf{y}}{\partial \mathbf{x}}{)}^2$显然与我们在直接优化$\mathbf{y}$时使用的$\frac{\partial L}{\partial \mathbf{y}}$不同。

牛顿法也不太好：我们首先计算像GD一样的一阶导数，然后计算完整过程的Hessian的二阶导数。但由于两者都是近似值，因此更新步骤产生的实际中间状态在评估完整链之前是未知的。在{doc}physgrad中，牛顿法的函数组合一致性段落中，Hessian的平方$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$项已经表明了这种依赖关系。

对于逆模拟器，我们没有这个问题：它们可以直接将$\mathbf{y}$空间中的点映射到$\mathbf{x}$空间中。因此，我们知道我们在$\mathbf{y}$空间中开始的位置，因为这个位置对于评估反演是至关重要的。

在本节的简单设置中，我们只有一个潜在空间，并且我们已经在优化过程中存储了所有的$\mathbf{x}$空间中的值（在history列表中）。因此，现在我们可以返回并重新评估physics_y以获取$\mathbf{y}$空间中的位置。

x = np.asarray([3.,3.])
eta = 0.01
historyGDy = []
historyNty = []

for i in range(1,10):
    historyGDy.append(physics_y(historyGD[i]))
    historyNty.append(physics_y(historyNt[i]))

historyGDy = onp.asarray(historyGDy)
historyNty = onp.asarray(historyNty)

axes = plt.figure(figsize=(4, 4), dpi=100).gca()
axes.set_title('y space')
axes.scatter(historyGDy[:,0], historyGDy[:,1], lw=0.5, marker='*', color='#1F77B4', label='GD')
axes.scatter(historyNty[:,0], historyNty[:,1], lw=0.5, marker='*', color='#FF7F0E', label='Newton')
axes.scatter(historyPGy[:,0], historyPGy[:,1], lw=0.5, marker='*', color='#D62728', label='PG')
axes.scatter([0], [0], lw=0.25, color='black', marker='*') 
axes.set_xlabel('z0'); axes.set_ylabel('z1'); axes.legend()

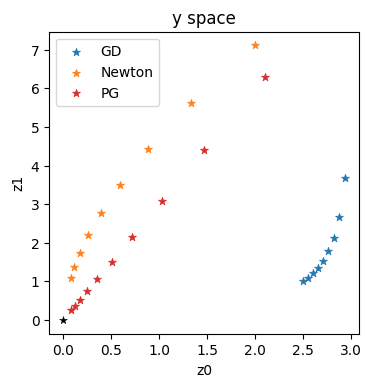
这些轨迹证实了前几节中所概述的直觉：蓝色的梯度下降在$\mathbf{y}$方向上给出了一个非常次优的轨迹。牛顿法（橙色）表现更好，但仍然明显弯曲。它不能很好地近似这个例子的高阶项。这与使用逆模拟器进行优化的直线和对角线红色轨迹形成对比。

当中间空间不仅仅是抽象的潜在空间，而是具有实际物理意义时，其行为变得尤为重要。

18.8 结论

尽管简单， 但这个例子已经显示出梯度下降、牛顿法和使用逆模拟器之间令人惊讶的大差异。

本节的主要要点如下。

• GD 很容易产生“不平衡”的更新， 并陷入僵局。
• 牛顿法做得更好， 但远非最优。
• 尽管只应用了部分 (我们上面仍然对 $L$ 使用了牛顿法)， 但逆模拟器的高阶信息优于两者。
• 此外，方法（一般来说是优化器的选择）对潜空间的研究进展也有很大影响，如上文𝑦 的情况所示。

在接下来的章节中， 我们可以基于这些观察结果， 通过可逆物理模型使用 PG 进行神经网络训练。

18.9 近似求逆

如果像上面的physics_y_inv_analytic这样的解析逆函数不容易得到，我们实际上可以采用优化方案，如牛顿法或BFGS，以数值方式获得局部逆函数。这是一个与不同优化方法的比较无关的主题，但可以基于上面的逆模拟器变体进行简单的说明。

下面，我们将使用scipy中的BFGS变体fmin_l_bfgs_b来计算逆函数。这并不是非常复杂，但我们将直接使用numpy和scipy，这使得代码有点混乱。

def physics_y_inv_opt(target_y, x_ini):
    # a bit ugly, we switch to pure scipy here inside each iteration for BFGS
    import numpy as np
    from scipy.optimize import fmin_l_bfgs_b
    target_y = onp.array(target_y)
    x_ini    = onp.array(x_ini)

    def physics_y_opt(x,target_y=[2,2]):
        y = onp.array( [x[0], x[1]*x[1]] ) # we cant use physics_y from JAX here
        ret = onp.sum( onp.square(y-target_y) )
        return ret
    
    ret = fmin_l_bfgs_b(lambda x: physics_y_opt(x,target_y), x_ini, approx_grad=True )
    #print( ret ) # return full BFGS details
    return ret[0]

print("BFGS optimization test run, find x such that y=[2,2]:")
physics_y_inv_opt([2,2], [3,3])

BFGS optimization test run, find x such that y=[2,2]:
array([2.00000003, 1.41421353])

尽管如此，我们现在可以使用这个数值反转的 $\mathbf{y}$ 函数来进行逆模拟器优化。除了调用 physics_y_inv_opt 函数外，其余代码保持不变。

x = np.asarray([3.,3.])
eta = 0.3
history = [x]; updates = []

Gy = jax.grad(loss_y)
Hy = jax.jacobian(jax.jacobian(loss_y))
for i in range(10):    
    # same as before, Newton step for L(y)
    y = physics_y(x)
    g = Gy(y)
    y += -eta * np.matmul( np.linalg.inv( Hy(y) ) , g)

    # optimize for inverse physics, assuming we dont have access to an inverse for physics_y
    x = physics_y_inv_opt(y,x)
    history.append(x)
    updates.append( history[-2] - history[-1] )
    print( "PG iter %d: "%i + format(x) )

PG iter 0: [2.09999967 2.50998022]
PG iter 1: [1.46999859 2.10000011]
PG iter 2: [1.02899871 1.75698602]
PG iter 3: [0.72029824 1.4699998 ]
PG iter 4: [0.50420733 1.22988982]
PG iter 5: [0.35294448 1.02899957]
PG iter 6: [0.24705997 0.86092355]
PG iter 7: [0.17294205 0.72030026]
PG iter 8: [0.12106103 0.60264817]
PG iter 9: [0.08474171 0.50421247]

这证实了近似求逆的有效性，与上述常规PG版本一致。没有太多意义来绘制这个，因为基本上是一样的，但我们可以测量差异。下面，我们计算了MAE，对于这个简单的例子，结果与我们的浮点精度相当。

historyPGa = onp.asarray(history)
updatesPGa = onp.asarray(updates) 

print("MAE difference between analytic PG and approximate inversion: %f" % (np.average(np.abs(historyPGa-historyPG))) )

MAE difference between analytic PG and approximate inversion: 0.000001

18.10 下一步

基于这个代码示例，你可以尝试以下修改：

• 用其他更复杂的函数替换上述简单的 L(y(x)) 函数。
• 用其他优化器替换简单的“常规”梯度下降，例如常用的 DL 优化器，如 AdaGrad、RmsProp 或 Adam。将现有版本与新轨迹进行比较。