前两节的讨论已经暗示了梯度反转是优化和学习的重要步骤。现在我们将把更新步骤整合到神经网络训练中,并详细介绍在之前的代码中已经使用的逆模拟器和牛顿步骤的双向过程。
如Scale-Invariance and Inversion中的 IG 部分所概述的,我们将重点放在下面的逆问题的神经网络求解上。这意味着我们有,我们的目标是训练一个神经网络表示,使得。这是一个比我们之前考虑的可微物理(DP)训练更为受限的设置。另外,由于我们现在的目标是优化算法,我们不会明确地表示DP方法:以下所有的变体都涉及物理模拟器,梯度下降(GD)版本以及其变体(如Adam)都使用DP训练。
需要记住的重要一点是:与前面的部分和{doc}
overview-equations相反,我们的目标是逆问题,因此是网络的输入:。相应地,它输出。
这给出了以下最小化问题,其中表示小批量的索引:
19.1 神经网络训练
为了将方程(24) 中的更新步骤整合到神经网络的训练过程中,我们考虑三个组成部分:神经网络本身、物理模拟器和损失函数。
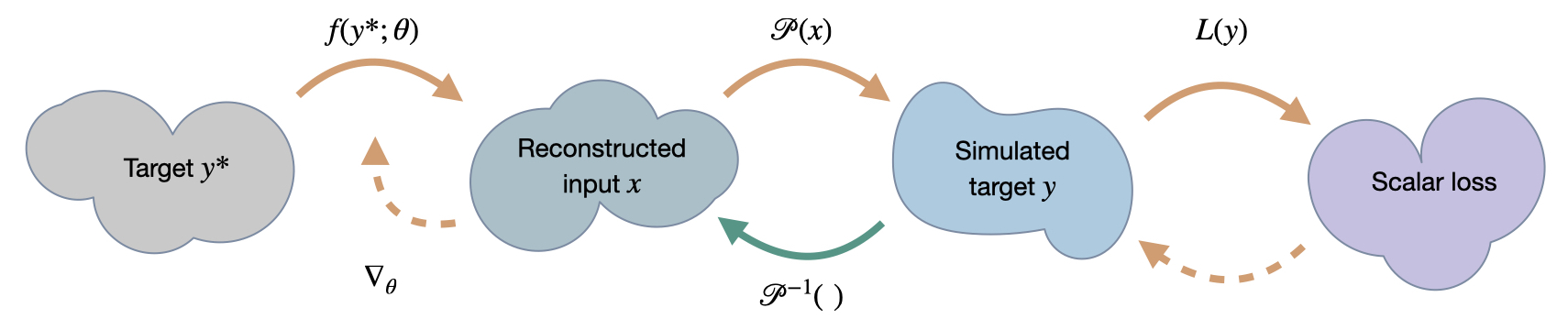
为了将这三个部分结合起来,我们使用以下算法。正如Holl等人在{cite}holl2021pg中介绍的那样,我们将把这个训练过程称为“尺度不变物理”(SIP)训练。
尺度不变物理 (SIP)训练:
为了更新神经网络的权重,我们执行以下更新步骤:
- 给定一组输入,通过前向传播计算神经网络的预测
- 通过前向模拟计算(),并调用(局部)逆模拟器获得步长,其中
- 计算网络损失,例如,其中,并进行牛顿步骤,将视为常数
- 使用梯度下降(或类似Adam的基于梯度下降的优化器)将的变化传播到网络权重,学习率为
该组合优化算法依赖于网络的学习率和上述步长,它影响到。一阶近似下,网络权重的有效学习率为。我们建议将设置为反向模拟器精度允许的最大值。在许多情况下,可以设置,否则应相应调整。这样可以最大限度地利用模拟器的非线性来调整优化方向。
该算法将反向模拟器与传统的神经网络训练方案相结合,以计算准确的高阶更新。这是一个有吸引力的特性,因为我们有一系列强大的神经网络训练方法,这些方法在这种方式下仍然适用。损失函数在神经网络和物理组件之间的处理在这里起着核心作用。

19.2 损失函数
在上述算法中,我们假设了一个损失,并且在没有进一步解释的情况下引入了牛顿步骤来传播逆模拟器步骤到神经网络。下面,我们将更详细地解释和证明这种处理方法。
引入牛顿步骤的核心原因是提高损失导数的准确性。与常规的牛顿方法或方程{eq}quasi-newton-update中的拟牛顿方法不同,我们不需要完整系统的Hessian矩阵。相反,Hessian矩阵仅对需要。这使得牛顿方法再次具有吸引力。更好的是,对于许多典型的函数,牛顿更新的解析形式是已知的。
例如,考虑最常见的监督学习目标函数 ,如上文所述。其中 表示预测值, 表示目标值。我们有 和 。使用方程 {eq}quasi-newton-update,我们得到 ,可以立即计算,无需评估任何额外的 Hessian 矩阵。
确定 后,可以使用逆模拟器 将梯度反向传播到 ,例如一个较早的时间。我们已经在 {doc}physgrad-comparison 中使用了这种损失的牛顿步骤和 PDE 的逆模拟器的组合。
这里的上的损失作为一个“代理”来嵌入逆模拟器的更新到网络训练流程中。它不应与传统的空间中的监督损失混淆。由于对预测的依赖性,它不会将空间中的多个解模式进行平均。为了证明这一点,考虑使用GD作为逆模拟的求解器的情况。然后,总损失纯粹在空间中定义,简化为常规的一阶优化。
因此,总结起来,我们在的损失中使用一个平凡的牛顿步骤,并在上使用一个代理损失,将逆物理和神经网络的计算图连接起来进行反向传播。下图可视化了不同的步骤。

19.3 迭代和时间依赖性
以上过程描述了优化使单个预测的神经网络的方法。这适用于在给出时系统状态的重构,或者估计一个在时满足特定条件的最佳初始状态。
然而,SIP方法也可以应用于涉及多个目标和不同时间点的多个网络交互的更复杂设置。这种情况常出现在控制任务中,其中网络在每个时间步骤诱导小力以达到时的特定物理状态。它也出现在校正任务中,网络试图通过在每个时间步骤执行校正来提高模拟质量。
在这些情况下,上述过程(损失的牛顿步骤,物理的逆模拟器步骤,神经网络的梯度下降)会迭代重复,例如在不同时间步骤中进行,导致中一系列加法项。 这通常使学习任务更加困难,因为我们需要反复反向传播物理求解器和神经网络的迭代,但上述SIP算法就像常规的梯度下降训练一样适用于这些情况。
19.4 SIP 训练实例
让我们通过一个示例来说明SIP训练的收敛行为以及它如何取决于的特性{cite}holl2021pg。我们考虑合成的二维函数:
其中表示旋转矩阵。参数和允许我们连续地改变系统的特性。的值决定了的条件,大的表示病态问题,而描述了和的耦合。当时,Hessian矩阵的非对角线元素消失,问题分解为两个独立的问题。
以下是,,的结果损失函数示例,显示了对于的正弦函数和的线性变化的交织:
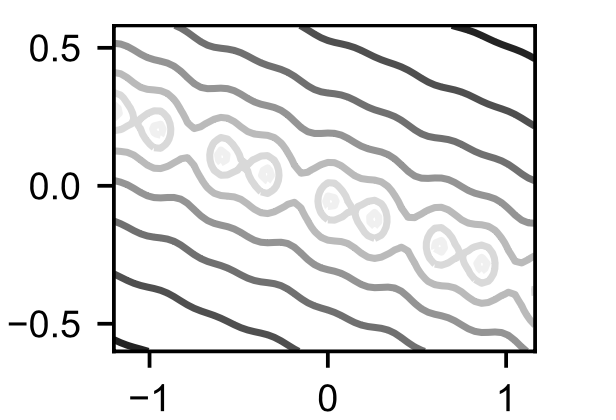
接下来,我们使用全连接神经网络通过方程{eq}eq:unsupervised-training来反演这个问题。我们将比较使用无鞍牛顿求解器的SIP训练和各种最先进的网络优化器。
为了公平起见,每个优化器都独立选择最佳学习率。当选择时,问题是完美的条件。在这种情况下,所有网络优化器都收敛,Adam略有优势。这在左图中显示:
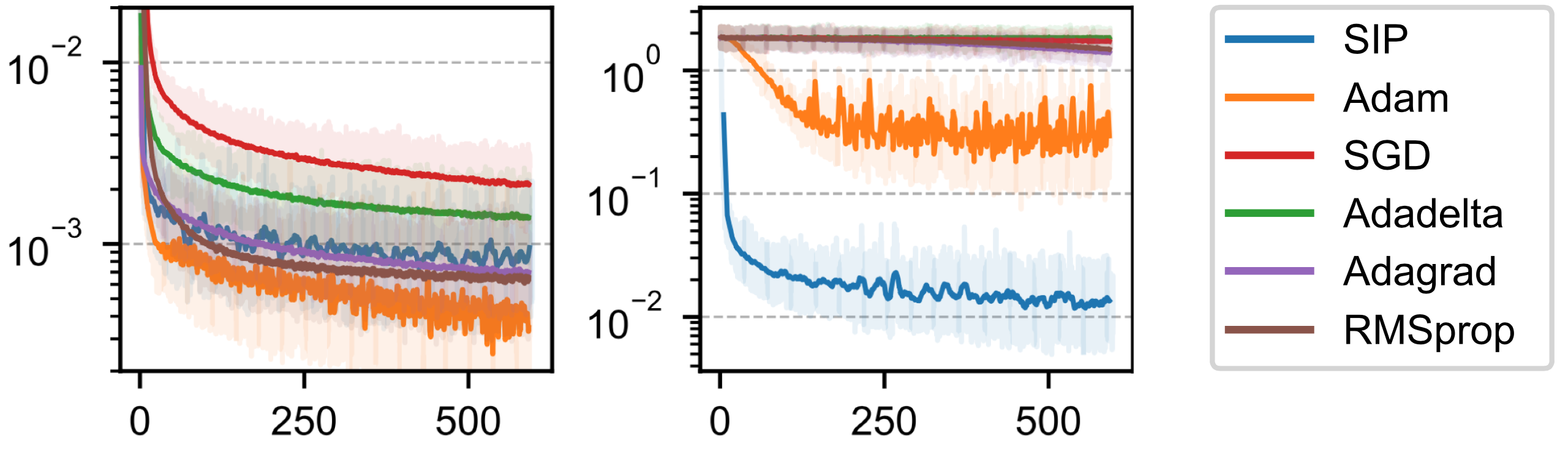
在时,我们有一个相当糟糕的条件情况,只有SIP和Adam成功地对网络进行了显著程度的优化,如右图所示。
请注意,上面的两个图显示了随时间的收敛情况。SIP的相对较慢收敛主要是因为每次迭代所需的时间明显比其他方法长,平均需要的时间是Adam的3倍。虽然Hessian矩阵的评估本质上需要更多的计算,但通过优化计算过程,SIP的每次迭代时间可能会显著减少。
通过增加而保持不变,我们可以展示条件不断影响不同方法的情况,如左图所示。
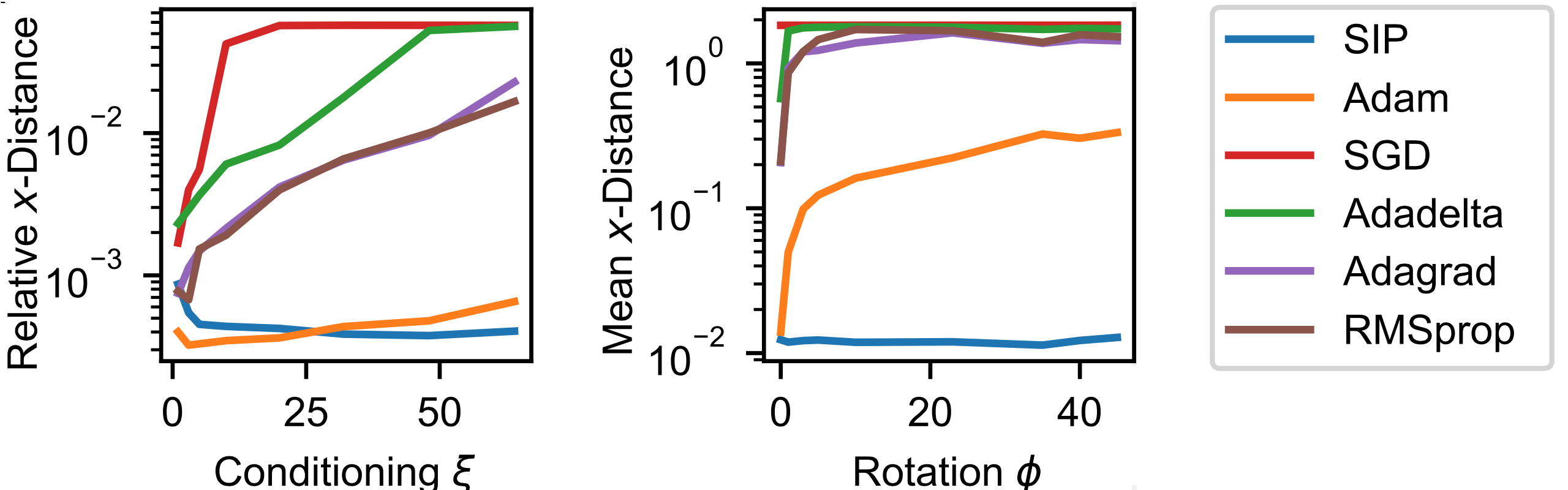
所有传统的网络优化器的准确性都会降低,因为梯度与中的成比例,导致在需要更精确值的方向上变得更长。SIP训练通过使用Hessian矩阵来避免这种情况,反转了缩放行为,并产生与中的平坦方向对齐的更新。这使得SIP训练在广泛的范围内保持相对准确性。即使对于Adam优化器,当变大时准确性也会变差。
通过仅变化,我们可以展示不同组件之间的交织如何影响优化器的行为。{numref}physgrad-sin-add-graphs的右图保持不变,变化。这揭示了Adam如何在病态设置中学习。当和处于不同尺度时,Adam通过对Hessian矩阵进行对角线近似来减小缩放效应,但当参数耦合时,缺少非对角线项阻止了这一点。在这种情况下,其性能下降了一个数量级以上。SIP训练对于耦合参数没有问题,因为其优化更新步骤使用了全秩Hessian矩阵。因此,SIP训练在这个示例设置提出的不同优化问题中产生了最佳结果。

19.5 对 SIP 训练的讨论
虽然我们目前只研究了较小的玩具问题,但我们将推进对SIP训练的讨论。下一章将通过一个更复杂的例子来说明这一点,但由于我们随后将直接切换到一个新的算法,因此下面是一个更好的地方来讨论SIP的性质。
总体而言,SIP训练的尺度不变性使其能够在许多物理问题上以指数级速度找到解决方案,同时保持相对较低的计算成本。当每次求解器评估都执行了足够的网络更新时,可以证明它能够收敛,并且可以证明它在广泛的物理实验中通过单个更新也能够收敛。
19.5.1 局限性
SIP训练可以找到更准确的解,但也有一些需要考虑的注意事项。
首先,需要一个大致尺度不变的物理求解器。在低维度的空间中,牛顿法是一个很好的选择,但在高维空间中需要其他形式的反演。有些方程可以在局部解析反演,但对于复杂问题,可能需要特定领域的知识,或者可以采用数值方法(即将要讨论的内容)。
其次,SIP侧重于对物理部分进行准确的反演,但使用传统的一阶优化器来确定。正如讨论过的,这些求解器在病态环境中表现不佳,这也会影响到SIP在网络输出在非常不同的尺度上的表现。因此,我们应该将反演NN作为目标。
第三,虽然SIP训练通常会导致更准确的解,但在空间中测量,对于损失来说并不总是如此。SIP训练平等地权衡所有示例,而不考虑它们的损失值。这可能是有用的,但在具有过度小或大曲率区域的示例中,会扭曲样本的重要性。在这些情况下,或者当空间中的准确性不重要时,例如在控制任务中,传统的训练方法可能比SIP训练表现更好。
19.5.2 与监督训练的相似之处
有趣的是,SIP训练类似于{doc}supervised中的监督方法。它有效地提供了一种可靠的更新方法,该方法在训练时实时计算。反向模拟器提供所需的反演,可能采用高阶方法,并避免了多模态解的平均化(参见{doc}intro-teaser)。
这是此设置的主要优点之一:预先计算的数据集无法考虑多模态性,因此一旦从输入到参考解的映射不唯一,就会不可避免地导致学习到次优解。同时,这也说明了{doc}diffphys中DP训练的一个困难之处:它产生的梯度没有得到适当的反演,并且很难通过预处理可靠地进行归一化。因此,在训练时可能会出现{doc}physgrad中讨论的缩放问题,并相应地给出消失和爆炸梯度。这些问题是本章要解决的问题。
在下一节中,我们将展示一个更复杂的例子,使用来自逆向模拟器的SIP更新来训练基于物理的神经网络,然后解释另一种求解规模问题的替代方法。