现在我们转向一个实际的例子，使用尺度不变物理（SIP）更新来处理更复杂的问题，具体而言，我们将考虑热方程，它提出了一些特别有趣的挑战：可微物理（DP）梯度只是扩散更多，而反演在数值上是具有挑战性的。下面，我们将解释SIP是如何解决前者的，而特殊的求解器可以解决后者的问题。

下面的笔记本提供了通过phiflow进行完整实现的数据生成、运行DP版本和计算改进的SIP更新的方法。

20.1 问题描述

我们考虑一个由热传导方程 $\frac{\partial u}{\partial t} = ν \cdot \nabla^{2} u$ 控制的二维系统。给定在 $t_{0}$ 时刻的初始状态 $x = u (t_{0})$ ，模拟器通过 $y = u (t_{*}) = P (x)$ 计算出后续时刻 $t_{*}$ 的状态。对于 $t \cdot ν = 0$ ，可以精确反演这个系统，但对于较大的 $t \cdot ν$ ，反演过程变得越来越不稳定，因为初始不同的热量水平会随着时间的推移逐渐平均，使原始信息淹没在噪声中。因此，物理学的雅可比矩阵 $\frac{\partial y}{\partial x}$ 接近奇异。

我们将使用周期边界条件，并在频率空间中计算结果，物理学可以通过 $\overset{y}{^} = \overset{x}{^} \cdot e^{- k^{2} (t_{*} - t_{0})}$ 进行解析计算，其中 $\overset{y}{^}_{k} \equiv F (y)_{k}$ 表示傅里叶变换向量 $y$ 的第 $k$ 个元素。在常规的正向模拟中，高频率成分以指数方式衰减。我们需要重新考虑逆模拟器中的这个方面。

总结起来，我们所追求的反演问题可以写成最小化： $L (x) = ∣∣ P (x) - y^{*} ∣ ∣_{2}^{2} = ∣∣ F^{- 1} (F (x) \cdot e^{- k^{2} (t_{*} - t_{0})}) - y^{*} ∣ ∣_{2}^{2}$

20.2 实现

下面，我们将在一个由64x64个单位长度的单元格组成的域上设置 $t \cdot ν = 8$ 。这种扩散水平具有挑战性，会耗散大部分细节，同时保留大尺度结构。

我们将使用phiflow作为默认后端的PyTorch，但是这个示例代码同样可以在TensorFlow上运行（只需在下面切换到phi.tf.flow）。

!pip install --upgrade --quiet phiflow==2.2
#!pip install --upgrade --quiet git+https://github.com/tum-pbs/PhiFlow
from phi.torch.flow import *    # switch to TF with "phi.tf.flow"

20.3 数据生成

对于训练，我们通过在域中随机放置4到10个随机大小和形状的“热”矩形来生成 $x^{*}$ 。下面的generate_heat_example()函数生成一个完整的小批量（通过shape.batch）的示例位置。这些位置将在后面作为 $x$ 。它们不会传递给求解器，但应该由神经网络进行重构。

def generate_heat_example(*shape, bounds: Box = None):
    shape = math.merge_shapes(*shape)
    heat_t0 = CenteredGrid(0, extrapolation.PERIODIC, bounds, resolution=shape.spatial)
    bounds = heat_t0.bounds
    component_counts = math.to_int32(4 + 7 * math.random_uniform(shape.batch))
    positions = (math.random_uniform(shape.batch, batch(components=10), channel(vector=shape.spatial.names)) - 0.5) * bounds.size * 0.8 + bounds.size * 0.5
    for i in range(10):
        position = positions.components[i]
        half_size = math.random_uniform(shape.batch, channel(vector=shape.spatial.names)) * 10
        strength = math.random_uniform(shape.batch) * math.to_float(i < component_counts)
        position = math.clip(position, bounds.lower + half_size, bounds.upper - half_size)
        component_box = Cuboid(position, half_size)
        component_mask = SoftGeometryMask(component_box)
        component_mask = component_mask.at(heat_t0)
        heat_t0 += component_mask * strength
    return heat_t0

数据是在训练过程中动态生成的，但现在让我们使用phiflow的vis.plot函数来查看两个示例 $x$ ：

vis.plot(generate_heat_example(batch(view_examples=2), spatial(x=64, y=64)));

20.4 可微分物理和梯度下降

到目前为止，这个设置并没有阻止我们使用在{doc}diffphys中描述的常规动态规划（DP）训练方法。

对于这个扩散情况，我们可以以解析方式写出梯度下降更新公式，如下所示： $Δ x_{GD} = - η \cdot F^{- 1} (e^{- k^{2} (t_{*} - t_{0})} F (y - y^{*}))$

观察这个表达式，它意味着使用可微分模拟器的梯度下降（GD）将前向物理应用于梯度向量本身。这是令人惊讶的：前向模拟执行扩散，而现在反向传播执行更多的扩散，而不是以某种方式撤消扩散？不幸的是，这是DP的固有且“正确”的行为，它导致更新是稳定的但缺乏高频空间信息。因此，在拟合粗糙结构之后，基于GD的优化方法在这个任务上收敛缓慢，并且在恢复高频细节方面存在严重问题，如下所示。

这不是因为信息本质上缺失，而是因为GD无法充分处理高频细节。

对于下面的实现，我们将简单地使用y = diffuse.fourier(x, 8., 1)进行前向传递，然后类似地计算两个应用了diffuse.fourier( , 8., 1)的 $y$ 场的 $L^{2}$ 损失。

20.5 稳定的 SIP 梯度

在本章的背景下，更有趣的是通过逆向模拟器计算得到的改进更新步骤，即SIP更新。与前面的章节一致，我们将称此更新为 $Δ x_{PG}$ 。

热方程的频率形式可以通过解析求逆，得到 $\overset{x}{^}_{k} = \overset{y}{^}_{k} \cdot e^{k^{2} (t_{*} - t_{0})}$ 。这使我们能够定义更新步骤。 $Δ x_{PG} = - η \cdot F^{- 1} (e^{k^{2} (t_{*} - t_{0})} F (y - y^{*}))$

在这里，高频率被指数级的因子所乘，导致数值不稳定性。直接将这个公式应用于梯度时，可能会导致 $Δ x_{PG}$ 的大幅波动。

请注意，即使在实际空间而非频率空间计算梯度时，这些数值不稳定性也会出现。然而，频率空间使我们更容易量化这些不稳定性。

现在，我们可以利用我们对物理模拟过程的了解来构建一个稳定的逆过程：通过采取概率观点，可以避免数值不稳定性。观察值 $y$ 包含一定量的噪声 $n$ ，其余部分构成信号 $s = y - n$ 。对于噪声，我们假设其服从正态分布 $n \sim N (0, ϵ \cdot y)$ ，其中 $ϵ > 0$ ；对于信号，我们假设其来自于合理的 $x$ 值，以使 $y \sim N (0, δ \cdot e^{- k^{2}})$ ，其中 $δ > 0$ 。有了这个，我们可以使用贝叶斯定理估计一个观察值来自信号的概率 $p (s ∣ v) = \frac{p ( v ∣ s ) \cdot p ( s )}{p ( v ∣ s ) \cdot p ( s ) + p ( v ∣ n ) \cdot p ( n )}$ ，其中我们假设先验 $p (s) = p (n) = \frac{1}{2}$ 。基于这个概率，我们抑制逆物理的放大，从而得到一个稳定的逆过程。

以这种方式计算的梯度保留了尽可能多的高频信息，考虑到存在的噪声。这比任何通用优化方法都具有更快的收敛速度和更精确的解决方案。下面的单元格实现了这种概率方法，其中apply_damping()中的probability_signal包含要抑制的信号部分。inv_diffuse()函数使用它来计算一个稳定的逆扩散过程。

def apply_damping(kernel, inv_kernel, amp, f_uncertainty, log_kernel):
    signal_prior = 0.5
    expected_amp = 1. * kernel.shape.get_size('x') * inv_kernel  # This can be measured
    signal_likelihood = math.exp(-0.5 * (abs(amp) / expected_amp) ** 2) * signal_prior  # this can be NaN
    signal_likelihood = math.where(math.isfinite(signal_likelihood), signal_likelihood, math.zeros_like(signal_likelihood))
    noise_likelihood = math.exp(-0.5 * (abs(amp) / f_uncertainty) ** 2) * (1 - signal_prior)
    probability_signal = math.divide_no_nan(signal_likelihood, (signal_likelihood + noise_likelihood))
    action = math.where((0.5 >= probability_signal) | (probability_signal >= 0.68), 2 * (probability_signal - 0.5), 0.)  # 1 sigma required to take action
    prob_kernel = math.exp(log_kernel * action)
    return prob_kernel, probability_signal


def inv_diffuse(grid: Grid, amount: float, uncertainty: Grid):
    f_uncertainty: math.Tensor = math.sqrt(math.sum(uncertainty.values ** 2, dim='x,y'))  # all frequencies have the same uncertainty, 1/N in iFFT
    k_squared: math.Tensor = math.sum(math.fftfreq(grid.shape, grid.dx) ** 2, 'vector')
    fft_laplace: math.Tensor = -(2 * np.pi) ** 2 * k_squared
    # --- Compute sharpening kernel with damping ---
    log_kernel = fft_laplace * -amount
    log_kernel_clamped = math.minimum(log_kernel, math.to_float(math.floor(math.log(math.wrap(np.finfo(np.float32).max)))))  # avoid overflow
    raw_kernel = math.exp(log_kernel_clamped)  # inverse diffusion FFT kernel, all values >= 1
    inv_kernel = math.exp(-log_kernel)
    amp = math.fft(grid.values)
    kernel, sig_prob = apply_damping(raw_kernel, inv_kernel, amp, f_uncertainty, log_kernel)
    # --- Apply and compute uncertainty ---
    data = math.real(math.ifft(amp * math.to_complex(kernel)))
    uncertainty = math.sqrt(math.sum(((f_uncertainty * kernel) ** 2))) / grid.shape.get_size('x')  # 1/N normalization in iFFT
    uncertainty = grid * 0 + uncertainty
    return grid.with_values(data), uncertainty, abs(amp), raw_kernel, kernel, sig_prob

20.6 神经网络和损失函数

对于神经网络，我们使用简单的U-net架构来处理SIP，以及常规的DP+Adam版本（与前面的部分一致，我们将其表示为“GD”）。我们使用批量大小为128和恒定学习率 $η = 1 0^{- 3}$ 进行训练，对于物理部分使用64位精度，对于网络部分使用32位精度。网络更新使用TensorFlow或PyTorch的自动微分计算。

math.set_global_precision(64)
BATCH = batch(batch=128)
STEPS = 50

math.seed(0)
net = u_net(1, 1)
optimizer = adam(net, 0.001)

现在我们将为phiflow定义损失函数。网络权重的梯度总是计算为 $d (loss_function) / d θ$ 。

对于SIP，我们反演物理过程，然后将代理损失定义为 $L^{2}$ (prediction - correction)，其中correction被视为常数。通过x = field.stop_gradient(prediction)来实现这一点。这个L2损失触发了对神经网络权重的反向传播。对于SIP，y_l2仅用于比较，对训练不是关键。

对于sip=False的Adam / GD版本，简单地计算预测的扩散 $y$ 场与目标之间的L2差异，并通过梯度传播操作进行反向传播。

我们还实时计算损失函数中的参考 $y = P (x^{*})$ 。

# @math.jit_compile
def loss_function(net, x_gt: CenteredGrid, sip: bool):
    y_target = diffuse.fourier(x_gt, 8., 1)
    with math.precision(32):
        prediction = field.native_call(net, field.to_float(y_target)).vector[0]
        prediction += field.mean(x_gt) - field.mean(prediction)
    x = field.stop_gradient(prediction)
    if sip:
        y = diffuse.fourier(x, 8., 1)
        dx, _, amp, raw_kernel, kernel, sig_prob = inv_diffuse(y_target - y, 8., uncertainty=abs(y_target - y) * 1e-6)
        correction = x + dx
        y_l2 = field.l2_loss(y - y_target)  # not important, just for tracking 
        loss = field.l2_loss(prediction - correction) # proxy L2 loss for network
    else:
        y = diffuse.fourier(prediction, 8., 1)
        loss = y_l2 = field.l2_loss(y - y_target) # for Adam we backprop through the loss and y
    return loss, x, y, field.l2_loss(x_gt - x), y_l2

20.7 训练

在训练循环中，我们通过generate_heat_example()实时生成数据，并使用phiflow的update_weights()函数调用所选择后端的正确函数。请注意，为了清晰起见，下面只打印了前5步的损失值，完整的历史记录保存在loss_列表中。下面的单元格运行SIP版本的训练：

loss_sip_x=[]; loss_sip_y=[] 
for training_step in range(STEPS):
    data = generate_heat_example(spatial(x=64, y=64), BATCH)
    loss_value, x_sip, y_sip, x_l2, y_l2 = update_weights(net, optimizer, loss_function, net, data, sip=True)
    loss_sip_x.append(float(x_l2.mean)) 
    loss_sip_y.append(float(y_l2.mean))
    if(training_step<5): print("SIP L2 loss x ; y: "+format(float(x_l2.mean))+" ; "+format(float(y_l2.mean)) )

SIP L2 loss x ; y: 187.2586057892786 ; 59.48433060883144
SIP L2 loss x ; y: 70.21347147390776 ; 13.783476203544797
SIP L2 loss x ; y: 51.91472605336263 ; 5.72813432496525
SIP L2 loss x ; y: 39.46109317565444 ; 4.4424629873554045
SIP L2 loss x ; y: 34.611490797378366 ; 3.359133206049436

现在我们可以使用Adam算法对DP版本进行训练，通过sip=False来禁用SIP更新。

math.seed(0)
net_gd = u_net(1, 1)
optimizer_gd = adam(net_gd, 0.001)

loss_gd_x=[]; loss_gd_y=[] 
for training_step in range(STEPS):
    data = generate_heat_example(spatial(x=64, y=64), BATCH)
    loss_value, x_gd, y_gd, x_l2, y_l2 = update_weights(net_gd, optimizer_gd, loss_function, net_gd, data, sip=False)
    loss_gd_x.append(float(x_l2.mean)) 
    loss_gd_y.append(float(y_l2.mean))
    if(training_step<5): print("GD L2 loss x ; y: "+format(float(x_l2.mean))+" ; "+format(float(y_l2.mean)) )

GD L2 loss x ; y: 187.2586057892786 ; 59.48433060883144
GD L2 loss x ; y: 104.37856249315794 ; 20.323700695817763
GD L2 loss x ; y: 72.5135221242247 ; 7.211550418534284
GD L2 loss x ; y: 59.74792697261851 ; 5.3912096056107135
GD L2 loss x ; y: 50.49939087445511 ; 3.6758429757536093

20.8 评估

现在我们可以直接比较这两个变体的表现。需要注意的是，由于随机数据的即时生成，所有样本都是之前未见过的，因此我们将直接使用训练曲线来得出这两种方法的性能结论。

下图显示了关于重建输入 $x$ 的 $L^{2}$ 误差在训练过程中的变化，这是我们训练的主要目标。

import pylab as plt
fig = plt.figure().gca()
pltx = range(len(loss_gd_x)) 
fig.plot(pltx, loss_gd_x , lw=2, color='blue',      label="GD")  
fig.plot(pltx, loss_sip_x  , lw=2, color='red', label="SIP")
plt.xlabel('iterations'); plt.ylabel('x loss'); plt.legend(); plt.yscale("log")

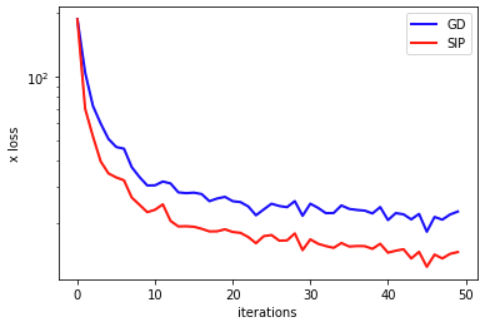
在 $x$ 的损失的对数尺度上，SIP版本的显著优势得到了很好的突出，表明了神经网络训练的收敛性显著改善。这纯粹是由于通过代理损失函数提供给物理学的更好信号所致。如loss_function()所示，两个变体都使用基于反向传播的更新方法来改变神经网络的权重。改进纯粹来自通过逆模拟器计算的 $y$ 空间中的高阶步骤。

出于好奇，我们还可以比较这两个版本在输出空间 $y$ 的差异方面的比较。

fig = plt.figure().gca()
pltx = range(len(loss_gd_y)) 
import scipy # for filtering
fig.plot(pltx, scipy.ndimage.filters.gaussian_filter1d(loss_gd_y,sigma=2)  , lw=2, color='blue',      label="GD")  
fig.plot(pltx, scipy.ndimage.filters.gaussian_filter1d(loss_sip_y ,sigma=2), lw=2, color='red', label="SIP")
plt.xlabel('iterations'); plt.ylabel('y loss'); plt.legend(); plt.yscale("log")

SIPs也有改进，但与 $x$ 空间相比，改进并不明显。幸运的是， $x$ 重建是主要目标，因此对于当前的逆问题而言，它具有更高的重要性。

通过直接比较， $L^{2}$ 误差方面的差异也非常明显。下面的单元格将GD和Adam的重建结果与SIP版本以及真实值进行对比。差异是显而易见的：SIP重建明显更锐利，且比GD版本包含更少的光晕。这是由于GD应用扩散到反向传播的梯度上，而不是与之相抵消的不良行为所导致的。

plt = vis.plot(x_gd.values.batch[0], x_sip.values.batch[0], data.values.batch[0], size=(15,4) )
plt.get_axes()[0].set_title("Adam"); plt.get_axes()[1].set_title("SIP"); plt.get_axes()[2].set_title("Reference");

20.9 下一步

针对此示例，值得尝试各种训练参数：延长训练时间，使用不同的学习速率和网络规模（甚至不同的体系结构）。